

 c语言实现一元线性回归
c语言实现一元线性回归
描述
第一:用所给样本求出两个相关变量的(算术)平均值
第二:分别计算分子和分母:(两个公式任选其一)分子
第三:计算b:b=分子/分母
用最小二乘法估计参数b,设服从正态分布,分别求对a、b的偏导数并令它们等于零。
先求x,y的平均值X,Y,再用公式代入求解:
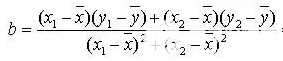
后把x,y的平均数X,Y代入a=Y-bX
求出a并代入总的公式y=bx+a得到线性回归方程
(X为xi的平均数,Y为yi的平均数)
#include
#include
void main()
{
float x[8] = {300.0 , 400.0 , 400.0 , 550.0 , 720.0 , 850.0 , 900.0 , 950.0};
float y[8] = {300.0 , 350.0 , 490.0 , 500.0 , 600.0 , 610.0 , 700.0 , 660.0};
int i;
int n;
float x_ave, y_ave, a, b, b1, mxy, sum_x, sum_y, lxy, xiSubSqr;
n = sizeof(x) / sizeof(x[0]);
a = b = mxy = sum_x = sum_y = lxy = xiSubSqr = 0.0;
for (i = 0; i < n; i++)
{
sum_x += x[i];
sum_y += y[i];
}
x_ave = sum_x / n;
y_ave = sum_y / n;
for (i = 0; i != n; i++)
{
lxy += (x[i] - x_ave) * (y[i] - y_ave);
xiSubSqr += (x[i] - x_ave) * (x[i] - x_ave);
}
b = lxy / xiSubSqr;
a = y_ave - b * x_ave;
printf("y=%0.2fx+%0.2f\n", b, a);
system("pause");
}
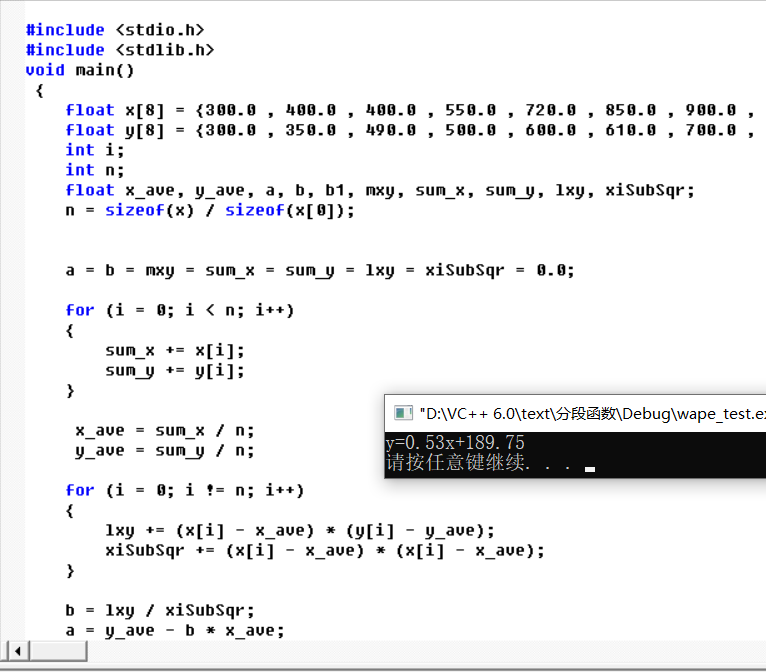
运行代码如下:
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
使用C语言解决一元二次方程的求根问题2023-09-04 2669
-
基于RK3568国产处理器教学实验箱操作案例分享:一元线性回归实验2024-12-05 1625
-
基于Proteus和C语言实现2021-07-14 942
-
如何用C语言实现一个简单的一元线性回归算法2021-07-20 1614
-
传感器网络中一种基于一元线性回归模型的空时数据压缩算法2010-03-06 884
-
C语言之求一元二次方程的根2016-04-22 609
-
C语言教程之一元钱的兑换方案问题2016-04-25 484
-
DSP算法的c语言实现2016-05-09 775
-
PID控制算法的C语言实现(完整版)2016-11-05 1268
-
matlab经典算法数字实验教程之回归分析2019-01-03 990
-
累加校验和C语言实现2021-11-29 814
-
怎么用C语言实现多态2022-10-12 2639
-
利用C语言实现高斯列主元消去法解线性方程组2022-12-02 3103
-
嵌入式开发的一元线性回归算法介绍2023-04-29 975
-
使用C语言实现的CRC计算单元的例子2024-05-16 2050
全部0条评论

快来发表一下你的评论吧 !

