

永磁同步电机的控制
描述
一、什么是力矩控制
永磁同步电机在汽车上的应用越来越广泛,从动力驱动到转向刹车的执行机构,都可以见到其踪影。今天想谈谈永磁同步电机的控制。
做控制的人都知道,任何电机的控制,无非三种不同的控制目标:
位置控制:想让电机转多少度它就转多少度
速度控制:想让电机转多快它就转多快
力矩控制:想让电机出多少力它就出多少力
但无论是哪种控制目标,无非是一个闭环还是两个闭环还是三个闭环的区别,力矩控制作为最内层的环,是必不可少的。今天就来讲讲什么是力矩控制?
要控制一个电机,首先对被控对象的了解是必须的。让我们用下面这张动图来帮助理解永磁同步电机是怎样运动起来的。定子三相上通过互差120度的交变电压以后,在定子铁芯上可以看到产生了旋转的磁场(动图中代表磁场方向的红绿颜色逆时针旋转),在这个旋转的磁场作用下,与转子磁场产生力的作用,带动转子旋转。
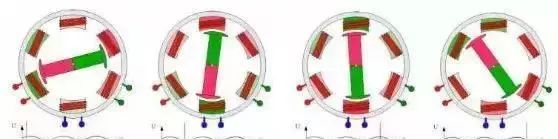
电机力矩是如何产生的呢?在前文《电机的力矩、转速和功率》,我们分析过力矩与电枢(定子)电流成正比;
那么电流是如何产生的呢?我们可以把电机的每一个绕组想象成一个在磁场中旋转的电阻+电感,如下面的等效电路:
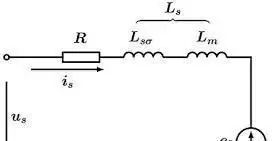
假设电机开环运行,当给定电机定子三相一个互差120度的电压建立起旋转磁场以后,如果这个时候没有负载,电机会飞速的转动起来(空载),直到反电势和给定电压完全相等;此时定子绕组中的电流为仍然为0,可以将定子的旋转磁场假想(虚拟/等效)成一个绕着电机轴心旋转的磁铁,假想出来的这块磁铁的南极与转子磁铁的北极轴线相重合;
当转子上有了负载以后,根据牛顿运动定理,电机的转速必然会有一个减速的过程,这就意味着上述等效电路中的反电势降低,而在给定电压不变的情况下,剩下的那些电压就会在电阻中产生电流了。在那这一段减速的过程当中还发生了什么事情呢?因为被负载拖拽了一下,转子磁铁的轴心比虚拟出来的定子磁铁轴心要之后一个角度了,这个角度就是我们所谓的“功角”。
关于电机的矢量模型,互联网上可以找到各种各样的图,但这些图要么太抽象,看了半天不知所云,没法和实物对照起来;要么不够全面,一张图里的内容有限,对实际工作指导意义不大。
因此笔者在实际工作过程中,喜欢把大量相关的矢量都揉在一起,见下图:
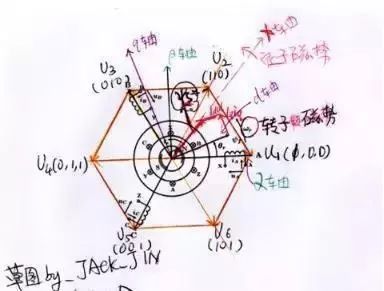
最中间的小圆是转子(N极和S极),转子外围有排列互差120度的AX,BY,CZ三相定子。
静止两相坐标轴:α与定子A相重合,β比α超前90度(图中绿色坐标轴)
旋转两相坐标找:d轴与转子的N极重合,q轴比d轴超前90度(图中紫色坐标轴)
X轴:定子旋转磁动势ψs,可分解为转子磁动势ψf,id*Lq和Iq*Ld(图中红色向量)
电压矢量:三相全桥的开关组合可以表示的电压在空间的表现形式(黄色箭头)
说一千,道一万,所谓的电机的力矩控制,就是通过一定的控制算法,去寻找一些开关管的组合(图中黄色部分)来合成一个给电机定子的给定电压(图中的大红色箭头),这个电压抵消掉反电势后产生的电流所对应的力矩刚好与外部负载平衡。
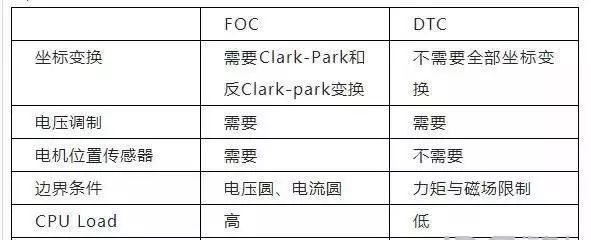
二、FOC与DTC
电机的力矩控制当前存在的两个主要流派是磁场定向控制FOC和直接转矩控制DTC,当然这两种控制的算法从原理上说对所有的交流电机都适用,本文只是讲讲他们用于永磁同步电机控制的异同。
FOC
FOC控制理论最初于上世纪70年代由西门子的工程师提出。在上文中我们提到过可以把定子所产生的磁场虚拟成一个绕转子高速旋转磁铁。
定子磁势可分解为d轴磁势和q轴磁势,d轴磁势与转子磁势同轴,不能产生切向的力矩,但会影响永磁同步电机转子永磁体所产生的磁场;q轴与转子磁势相差90度,因而产生切向的力矩(类似两根垂直的条形磁铁所产生的相互作用力)。
FOC的控制的基本思路就是将三相静止ABC坐标系下的相关变量转换到旋转坐标系下(d,q)进行数学运算,controller改变d轴和q轴的电压达到控制d轴和q轴电流的目的。然而最终给电机三相的只能是静止坐标系下的电压,因此在控制算法中需要再次把dq轴的电压转换成ABC三相电压给驱动桥。即存在一个从物理模型à数学模型à控制算法à物理模型的过程。
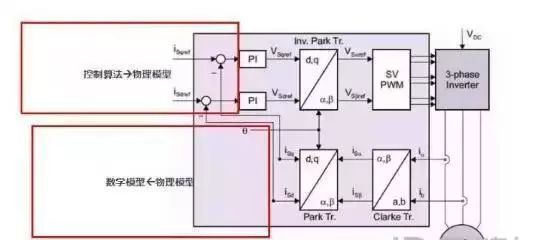
要实现FOC,下列输入必不可少:
1.电机三相电流(可采用如上图所示的的两个电流传感器,也可以采用一个低边或高边的母线电流传感器,用分时采样电流重构的方法还原出三相电流)
2.电机的位置信号缺一不可
下列控制模块必不可少:
1.Clark-Park变换
2.d轴和q轴的PI调节
3.反Clark-Park变换
4.SPWM/SVPWM(当然是用SVPWM)
下图给出了具体的控制过程。
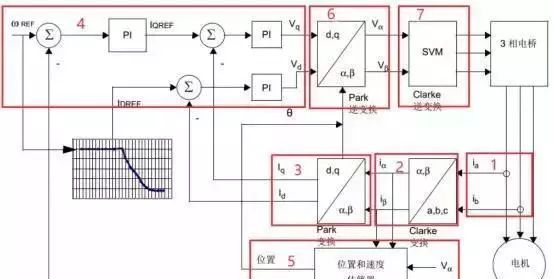
过程如下:
1、测量3相定子电流。这些测量可得到ia和ib的值,可以通过以下公式计算出ic:
ia+ib+ic=0
2、将3相电流变换至2轴系统。该变换将得到变量iα和iβ,它们是由测得的ia和ib以及计算出的ic值变换而来的。从定子角度来看,iα和iβ是相互正交的时变电流值。
3、按照控制环上一次迭代计算出的变换角,来旋转2轴系统使之与转子磁通对齐。iα和iβ变量经过该变换可得到Id和Iq。Id和Iq为变换到旋转坐标系下的正交电流。在稳态条件下,Id和Iq是常量。
4、误差信号由Id、Iq的实际值和各自的参考值进行比较而获得。
· Id的参考值控制转子磁通
· Iq的参考值控制电机的转矩输出
· 误差信号是到PI控制器的输入
· 控制器的输出为Vd和Vq,即要施加到电机上的电压矢量
5、估算出新的变换角,其中Vα、Vβ、iα和iβ是输入参数。新的角度可告知FOC算法下一个电压矢量在何处。
6、通过使用新的角度,可将PI控制器的Vd和Vq输出值逆变到静止参考坐标系。该计算将产生下一个正交电压值Vα和Vβ。
7、Vα和Vβ值经过逆变换得到3相值Va、Vb和Vc。该3相电压值可用来计算新的PWM占空比值,以生成所期望的电压矢量。
DTC:
DTC的出现比FOC晚了十多年,是上世纪80年代中期由德国学者Depenbrock教授提出。其基本思路是不再将定子侧的相关变量折算到转子的旋转坐标系下,放弃了矢量控制中电流解耦的控制思想 ,去掉了PI调节模块、反Clark-Park变换和SVPWM模块 ,转而通过检测母线电压和定子电流 ,直接计算出电机的磁链和转矩 ,并利用两个滞环比较器直接实现对定子磁链和转矩的解耦控制。
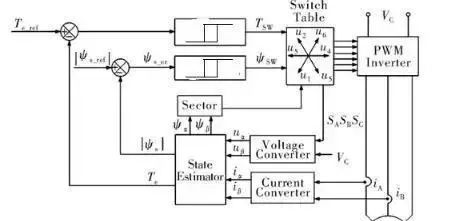
从上框图我们可看到,控制算法首先根据电机的线电流和相电压,得到在静止两相坐标轴下的电压和电流 Uα 、Uβ、 Iα、 Iβ。然后根据这四个量,对定子的磁通和力矩进行估计,怎么个估计法呢?可以用如下两个公式(不需要电机角度信号):
同时,还要根据电机定子的电压和电流来估算当前转子的位置所在的区间。
当然如果担心软件中积分运算有累计误差导致不准确,或者转子磁通的值不准确,或者功率角的值不准确,也可以在系统中加入角度传感器,将相关参数都放到旋转坐标dq轴坐标系下后去计算。
计算得到定子磁通和扭矩值以后,与其参考值做比较并经过滞缓比较器以后,得到两个非零即1的状态量,表征当前磁和力与参考值的关系其关系如下。

1.针对当前的力矩和磁场,不考虑到底磁场和力矩输出与参考值相差多少,只考虑他们是“欠”还是“过”
2.在控制策略中,不考虑每一次运行的时候都给一个准确的电压矢量,而是在每个运行周期内给出一个V1-V6其中之一(因此没有占空比这个概念存在了)
接下来的问题是怎样选择V1还是V6呢?还是先回到D-Q轴坐标系的这张图(虽然在控制中算法中不会用到),稍作思考即可想明白如果施加的电压向量与d轴在正负90度之内就会导致磁通增加;施加的电压向量与q轴在正负90度之内就会导致扭矩增加。
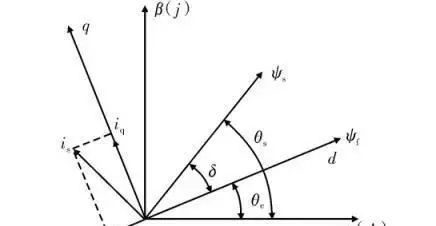
可以用下面极坐标系的四个象限来表示其关系:
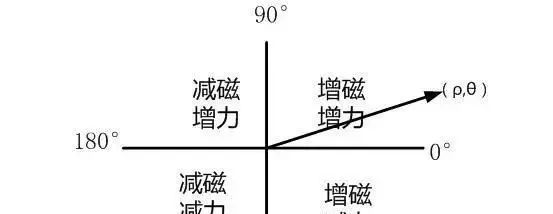
那么,我们就可以根据当前转子位置值,按以下开关表给电机驱动桥指令:
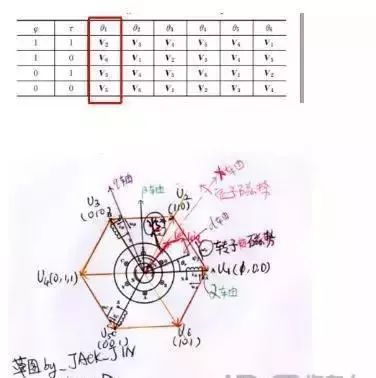
结合以上两图,以电机在第一扇区为例,
1.如果电机欠磁欠力(1 1),给定U2,则给定电压与电机当前位置的电压夹角介于[0° 60°]之间,实现增磁增力;
2.如果电机欠磁过力(1 0),给定U6,则给定电压与电机当前位置的电压夹角介于[-60° 0°]之间,实现增磁增力
3.如果电机过磁欠力(0 1),给定U3,则给定电压与电机当前位置夹角介于[60° 120°]之间,电机会增力,但磁的状况不单调,但是随着多个循环的调整,磁最终也能与给定平衡(这个是没有办法的事情,6个电压矢量把空间分成了6个区间;而增减关系是4个区间,必然有重叠)
4.如果电机过磁过力(0 0),给定U5,则给定电压与电机当前位置夹角介于[180° 240°]之间,电机减磁减力
其余区间类推,最终形成的定子磁链如下图所示:

综上,可对两种控制算法小结如下:
三、关于电机位置信号
电机位置信号的重要性
在永磁同步电机FOC控制算法中,需要用到一个非常重要的物理量是电机的位置信号。
这个位置信号到底有多重要呢?还是用数据来说话吧。笔者搭建了一个电机的电流环仿真模型,固定电机转速的情况下,给定电机3.2Nm的控制指令,
分三种工况进行仿真:
工况1:转子信号正常(下图绿线)
工况2:转子信号上叠加30度的偏置(下图蓝线)
工况3:转子信号上叠加±7度的高斯随机白噪声(下图红线)
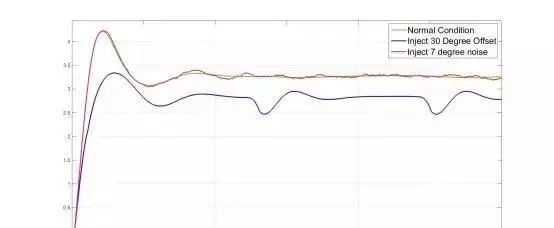
从仿真结果来看,工况2电机输出力矩不足且存在与转子位置相关的固有波动;工况3存在一定程度的扭矩纹波。由此,该信号的重要性可见一斑。
电机位置信号的种类
目前在汽车领域的电机里用得比较多的电机位置信号传感器有两种类型:
(1) 内外磁环+Hall芯片
这种方案会在电机端部与转子同轴处安装一磁环板,板上充有内磁环和外传两部分,同时在磁环附近安装有一PCB,PCB上安装有三个单线性hall芯片输出Hall_A,B,C信号和一个双线性Hall芯片输出Hall_Q1,Q2信号。
内磁环上分布与电机极对数相等均匀分布的N-S磁极,分别依次以120度相位差被三个单hall芯片感应。因而,对这三片hall芯片在PCB版上的排列要求就是这三个芯片应该在【0 360/极对数】范围内均匀分布。
外磁环上分布了若干N-S磁极(比较典型的数字是72,80),随着转子的转动N_S磁极每经过双Hall芯片下方一次,芯片感应输出一组正交90度变化的HallQ1_Q2信号。

比较典型的Hall信号与电机反电势的关系见下图:
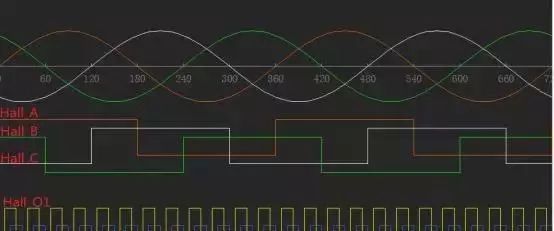
一般来说用五路信号足以得到电机绝对位置,并且他们之间具备相互冗余校验的功能。但是在一些要求比较高的场合,可能会用到7路hall信号。
(2) 旋转变压器
旋转变压器的定子绕组作为变压器的原边,接受励磁电压;转子绕组作为变压器的副边,通过电磁耦合得到感应电压。其工作原理和普通变压器基本相似,区别在于普通变压器的原边、副边绕组是相对固定的,所以输出电压和输入电压之比是常数,而旋转变压器的原边、副边绕组则随转子的角位移发生相对位置的改变,因而其输出电压的大小随转子角位移而发生变化。

其典型的信号特征如下:
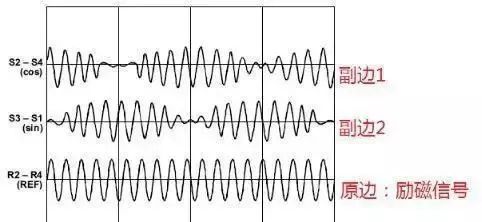
除此之外,近些年来磁阻型的位置信号传感风头正劲,大有抢班夺权之势。
电机位置信号的应用
Hall信号的一般经过一个简单的整形电路以后直接接入单片机的比较捕捉单元就可以被单片机进行解码,某些单片机甚至有专门的Hall信号正交编码单元由硬件实现对HallQ信号的解码;而旋变信号则需要专用的解码芯片(该专用解码芯片一般来说是指RDC resolver芯片,现在做的最好的就是美国的ADI和日本多摩川两家,但也不绝对,比如某日本厂商采用的就是一片运算单元功能强大但外设很少的MCU)。
审核编辑 :李倩
-
永磁同步电机控制笔记:中点平移法svpwm实现分析2023-03-13 1245
-
现代永磁同步电机控制原理及MATLAB仿真源码/模型2022-09-05 1273
-
浅谈永磁同步电机的控制2022-03-12 12962
-
永磁同步电机控制解析合集2022-01-24 2255
-
永磁同步电机控制原理2021-08-27 1720
-
有关永磁同步电机控制策略的代码2021-07-20 1073
-
基于矢量控制的永磁同步电机控制方法综述2021-06-29 1532
-
永磁同步电机控制模型搭建问题2017-08-20 5254
-
永磁同步电机控制参数设计方法2017-01-05 1145
-
基于TMS320LF2407的永磁同步电机控制2016-05-06 678
全部0条评论

快来发表一下你的评论吧 !

