

信号的对称性如何简化计算傅里叶系数
今日头条
描述
了解信号的对称性如何可以简化计算傅里叶系数时,用来找到电路的稳态响应
求一个波形的傅里叶级数系数往往涉及一些相对繁琐的计算。只有通过目视检查波形,不执行一个单一的计算,有时是可能的,以确定哪些系数将工作到零。当波形具有某种类型的对称性时,就可以做到这一点。请继续阅读,了解这些对称性,以及如何使用它们来简化傅里叶系数的计算。
理解傅里叶级数系数
下面的方程可以用来表示一个周期信号 f (t) ,周期 T 用它的傅里叶级数系数表示:
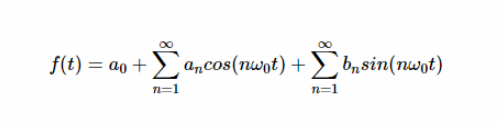
其中 a0,an 和 bn 是信号的傅里叶系数 ω
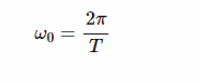
表示周期信号的基频。频率 nω0被称为波形的 n 次谐波。
这些系数可用下列公式计算:

等式1
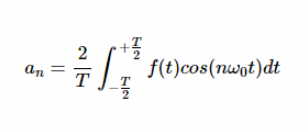
方程式2
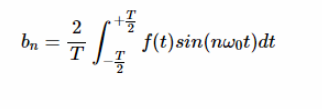
方程式3
让我们看看不同类型的对称是如何简化上述系数的计算的。
偶函数对称性
图1显示了一个周期 T 波形的例子,它甚至具有对称性。
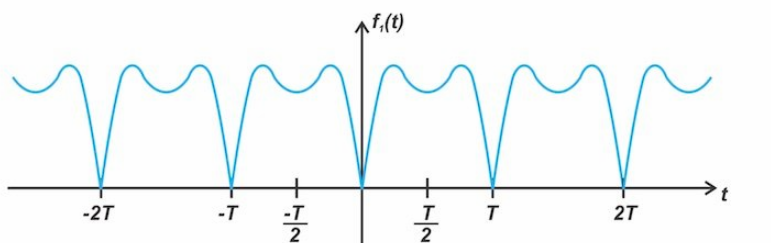
图1。一个周期为 T 的对称波形的例子
偶函数的图形是关于垂直轴(y 轴)对称的。在数学语言中,f (t)是即使它满足以下条件:
F (- t) = f (t)
偶数函数的一个熟悉的例子是 f (t) = cos (t) ,因为它为给定 t 的正值和负值产生相同的值。图2绘制了 f2(t) = cos (2πt)。
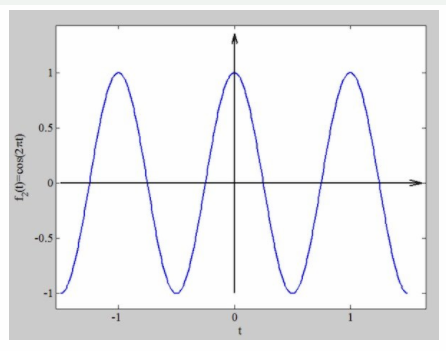
图2. f2(t) = cos (2πt)的函数图示例
另一个偶数信号如图3所示。
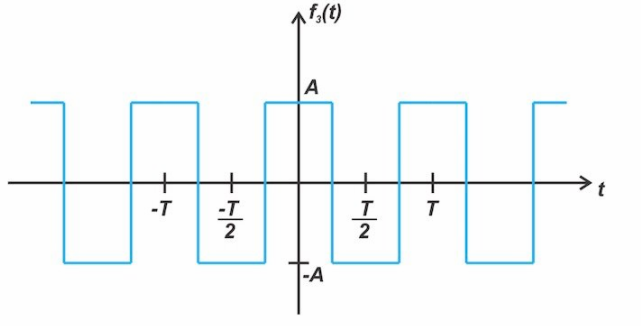
图3。偶数信号的一个例子
虽然图1和图3中的 f1(t)和 f3(t)具有偶对称性,但我们将很快讨论 f3(t)具有其他对称性水平,即半波对称性和四分之一波对称性。现在,只需要注意 f3(t)在其周期的后半部分,比如 T/2到 T 间隔,等于信号在前半周期(0到 T/2间隔)中的负值。
奇函数对称性
具有奇对称性的函数示例如图4所示。
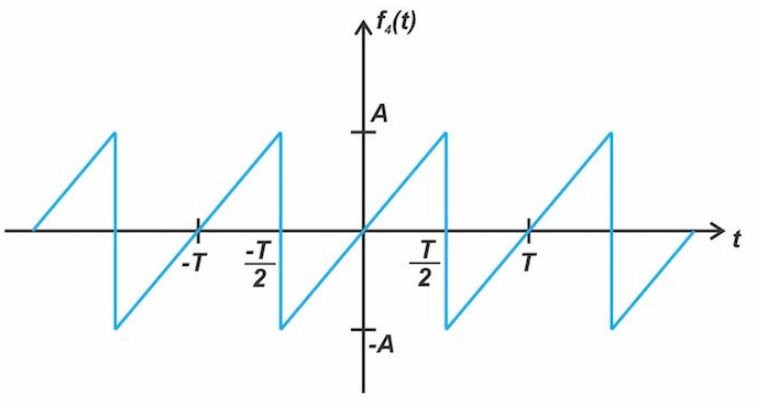
图4。一个奇对称的函数示例
奇函数的图是关于原点的对称图。如果 f (t)是一个奇函数,它满足以下条件:
F (- t) =-f (t)
与余弦不同,正弦函数是一个奇数函数。图5显示了 f (t) = sin (2πt)的曲线。
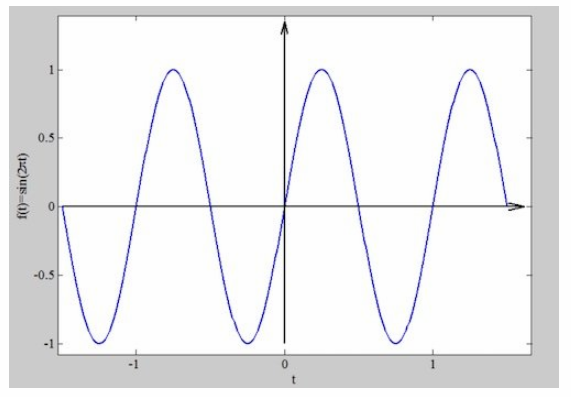
图5. f (t) = sin (2πt)的示例图形图函数
另一个示例如图6所示。
图6. 同一绘图的另一个图形示例
图4和图6所示的 f4(t)和 f5(t)都具有奇对称性,而 f5(t)也具有半波对称性和四分之一波对称性。请注意,f5(t)在其周期的后半段产生的值,比如 T/2到 T 间隔,等于信号在前半个周期(0到 T/2间隔)中获得的值的负值。
在讨论这些对称性对傅里叶系数的影响之前,让我们先看看计算信号的积分是如何受到偶对称性和奇对称性的影响的。
奇偶信号的积分
考虑在从-a 到 + a 的对称区间上积分偶数函数 f (t)。我们可以把这个积分写成从-a 到0和0到 + a 的两个积分之和,如下所示:
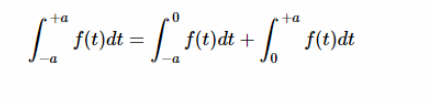
方程式4
之前,我们看到偶数函数是对称于 y 轴的。由于这种对称性,f (t)在-a 到0的区间下的面积与0到 + a 的区间下的面积相同。
因此,上述积分可重写为:
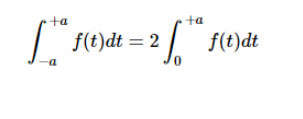
等式5
另一方面,如果我们假设 f (t)具有奇对称性,那么方程4中的积分就是零,因为-a 到0的区间的面积是0到 + a 区间的面积的负数。这意味着假设奇对称,我们得到:
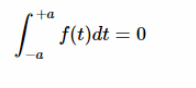
偶对称性对傅里叶级数的影响
如果 f (t)具有偶对称性,我们可以将方程1简化如下:
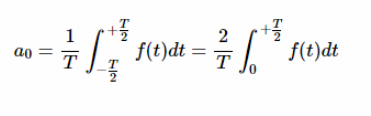
此外,如果 f (t)是偶数,可以很容易地验证 f (t) cos (nω0t)和 f (t) sin (nω0t)分别具有偶对称和奇对称。所以,
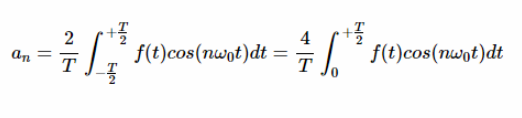
还有,
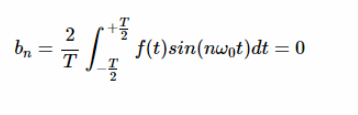
因此,对于偶数信号,所有的 bn 系数都为零。
奇对称性对傅里叶级数的影响
如果 f (t)具有奇对称性,则 f (t) cos (nω0t)和 f (t) sin (nω0t)分别具有奇对称性和偶对称性。
因此,方程式1至3简化为:
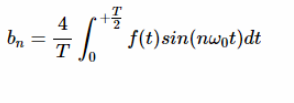
因此,对于奇数信号,所有的系数都为零。
半波对称性
在具有半波对称性的信号中,每个周期可分为两个半周期,其中两个半周期的形状完全相同,但相互颠倒。换句话说,第二个半周期与第一个半周期相同,是围绕水平轴(时间轴)倒转的。具有半波对称性的波形示例如图7所示。
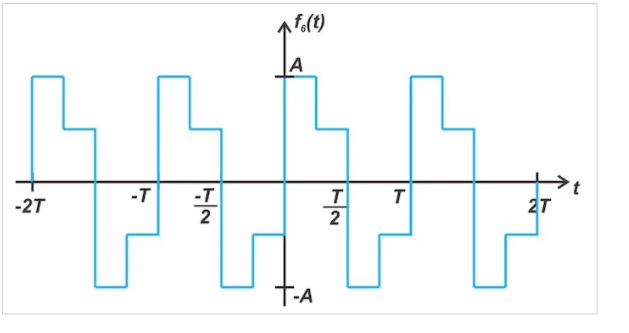
图7。一个半波对称波形的例子
在数学语言中,这一特征可以用以下条件来描述:
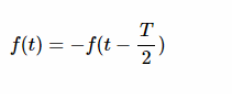
方程式6
这意味着如果我们将信号沿着时间轴移动 T/2并反转,我们将获得原始信号。
考虑到这一点,半波对称性将如何影响信号的傅里叶系数?
具有半波对称性的信号由相同的半周期和相反的极性组成。由于这种交替特征,我们可以得出结论,信号的平均值为零。所以半波对称消除了 a0系数,因为这个系数对应于信号的平均值。然而,计算其他系数有点复杂。
对于 a,我们从方程2开始,把积分分成两个区间:
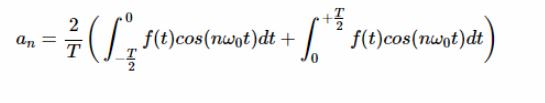
方程式7
现在,我们尝试用第二个积分来重写第一个积分,这样就可以考虑 f (t)的半波对称性。
我们可以定义一个新变量如下:
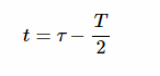
对于 t =-T/2和 t = 0,新的变量分别是 τ = 0和 τ = T/2。还注意到 dt = dτ,第一个积分可以重写为:
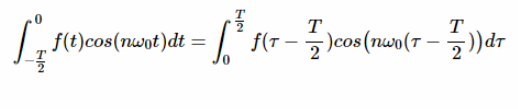
等式8
余弦项可简化如下:
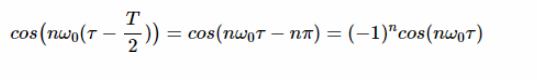
方程式9
应用半波对称性(方程6)和取代方程9,我们可以把方程8表示为:
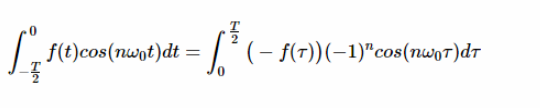
方程式10
对于奇数 n,上面的积分等于方程7中的第二个积分。然而,对于偶数 n,上面的积分等于该积分的负数。因此,对于具有半波对称性的信号,对于 n 的偶数值,系数为零。对于 n 的奇数值,我们有:
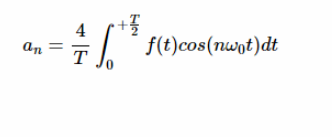
等式11
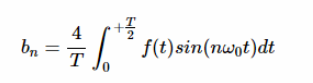
等式12
四分之一波对称性
当一个周期波形同时具有半波对称性和偶/奇对称性时,我们称之为四分之一波对称性。例如,图3中的波形既具有半波对称性,又具有均匀对称性。另一方面,图6中的波形是一个具有半波对称性的奇异信号。因此,这两个信号被称为具有四分之一波的对称性。
对于具有半波对称性的偶数信号,由于偶数对称性,所有 n 的 bn 系数都为零。此外,半波对称性使 a0和偶数 n 的 an 系数消失。因此,对于具有半波对称性的偶数信号,只有奇数 n 的系数可以是非零的。这些系数可以通过应用方程11找到,为方便起见,重复如下:
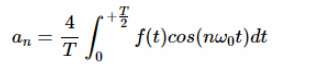
利用四分之一波对称性,信号在正负半周期的中点附近表现出对称性。因此,上述积分可简化为:
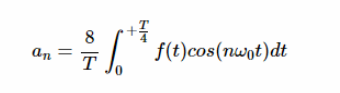
类似地,如果一个函数是奇数且具有半波对称性,则由于奇对称性,该函数的系数为零。同样,a0是零,因为半波信号的平均值为零。由于信号的半波对称性,只有奇数 n 的 bn 系数可以是非零的。对于单数 n,bn 由:
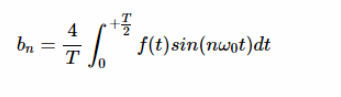
这也可以简化为:
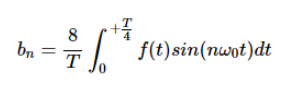
检查两种常见波形
考虑图8所示的锯齿波形。
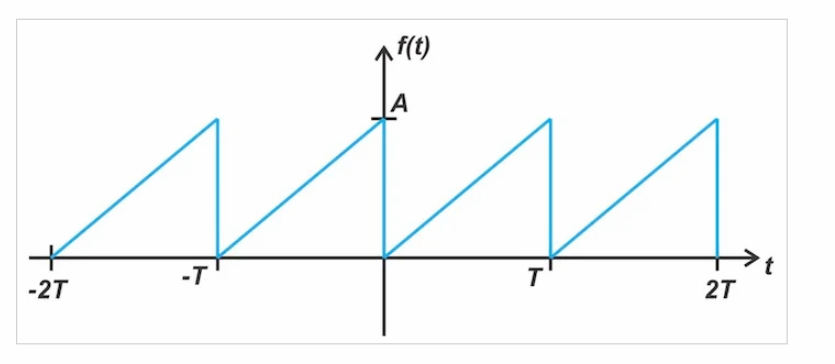
图8。锯齿波形的一个例子
使用方程1至3,上述波形可表示如下:
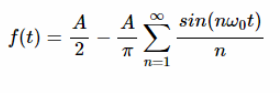
等式13
为了更容易地将波形与其傅里叶系数联系起来,让我们从信号中减去 DC 值,从而得到图9中的波形。
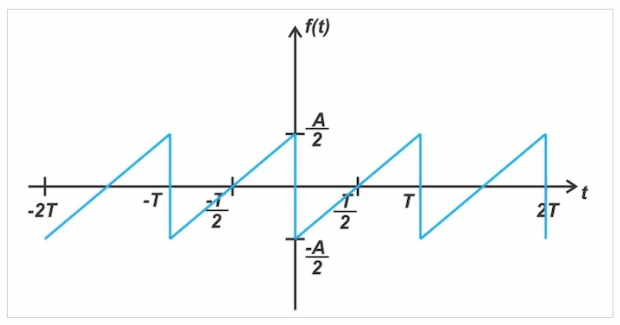
图9。从信号中减去 DC 值的奇函数波形实例
剔除直流值,得到一个奇函数。因此,我们可以得出结论,只有 bn 系数可以是非零的,这与方程13是一致的。作为最后一个示例,我们将查看如图10所示的三角波。
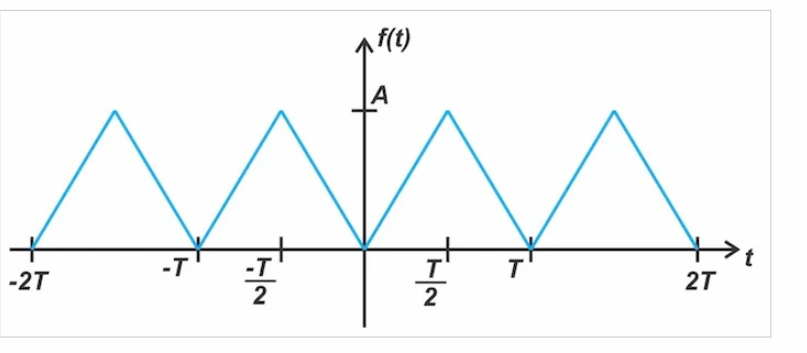
图10。一个示例三角波
函数的傅里叶级数表示如下:
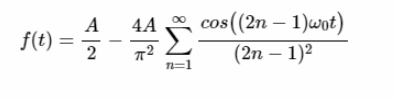
等式14
同样,通过减去平均值,我们可以得到图11中的波形。
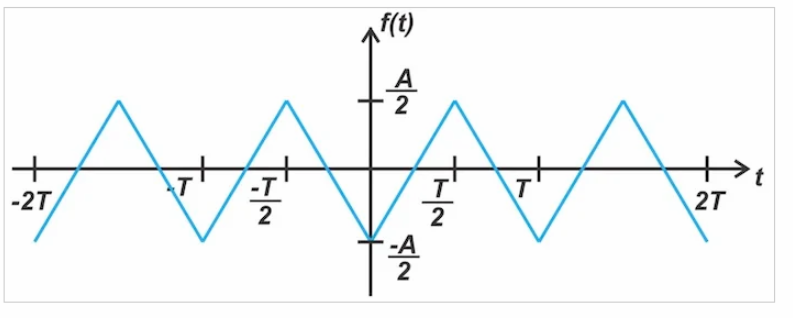
图11。半波对称波形
在这种情况下,我们得到了一个具有半波对称性的偶数信号。因此,对于所有 n,我们应该有 bn = 0; 对于偶数 n,我们应该有 an = 0。这与方程式14是一致的。
在本文中,我们探讨了不同类型的对称性对傅里叶系数的影响。有了这些知识,您现在应该能够预测当信号具有某种类型的对称性时,哪些系数将变为零。
审核编辑:汤梓红
-
运放的哪些参数可以反映出它的不对称性?2024-09-10 531
-
对称性加密算法2021-07-19 1621
-
对称性对傅里叶系数的影响2022-06-21 3075
-
基于几何对称性的颅骨复原技术2009-04-14 660
-
对称性和格点理论在矩量法中的应用2009-10-23 924
-
晶体对称性分析2010-08-26 783
-
机械结构对称性实例设计2018-03-10 1247
-
对称性对傅立叶系数的影响有哪些2019-09-01 6912
-
对称性和空间维度可对具有能隙的物态进行拓扑分类2020-06-09 3437
-
SHARC-Request评估码的DTS对称性2021-06-04 542
-
物质和反物质不对称性与CP对称性破缺2022-10-25 3214
-
关于麦克斯韦方程对称性的报告2022-11-07 1895
-
利用对称性化简求解对称电路2023-03-09 6815
-
如何证明波导正规模的电场磁场具有时间对称性和反对称性?2023-10-19 1418
-
通过交互式对称性校验提升集成电路设计流程2025-05-22 1430
全部0条评论

快来发表一下你的评论吧 !

