维度的拓扑

凝聚态物理中，有一些最基本的参量，其效用是普适的，并规范着一些最基本的物理性质。相信读者均认可，体系的时空维度，即为此中一元 (本文只限于空间维度)。

凝聚态系统中，维度是理解其物理的基本要素，从而被给予格外关注。物理人都将纳米科学的起源，与费曼于 1959 年在 APS 会议上所作的《底层的丰富》演说联系起来。我们猜，那时候费曼的心目中，“底层”应该就是低维，而不会只是指普通意义上的纳米颗粒或准零维体系。现在，我们早就耳熟能详凝聚态系统中维度的作用。

Ising 非此道中人，主要从书本中零存整取对维度的感受，如图 1 所示。对材料科学，也能随手举几个曾经听说过、或肤浅参与过的具体例子，与维度有一些内在的联系 (不追求准确，但追求“醒目”)：

(1) 晶粒长大：材料中晶粒长大或畴长大是普遍现象，但其物理未必简单。以各向同性体系中晶界能驱动的晶粒长大为例，其长大动力学就与维度密切相关。材料教科书很早就写明，1960 年代，Lifshitz、Slyozov 和 Wagner 三位学者在前人研究基础上，提出了那著名的、以其名字命名的晶粒长大 LSW 动力学理论：在等温条件下的晶粒长大后期，晶粒平均尺寸 R 与时间 t 之间满足 1/d 幂指数定律，这里 d 乃空间维度。也就是说，块体材料晶粒长大满足 1/3 幂律，准二维薄膜晶粒长大满足 1/2 幂律，虽然真正的一维线晶粒长大动力学还是一个问题。

因为实验体系掺杂了各种因素，这一规律的验证曾经很有曲折，引发过 1990 年代欧美物理学家和材料学家对此幂律的质疑。质疑之火前后延续十多年，最后还是被大规模计算模拟和精细实验验证所浇灭：1/d 幂律才是正确的。小编 以为这是材料科学史上维度胜出的一段佳话。

(2) 磁性：磁学中维度的意义更被彰显，并屡屡影响其发展进程。虽然磁学更多具有量子本质，但不妨碍对经典磁学的维度讨论。从 Ising 模型开始，一维模型不存在有限温度的相变，到二维模型那著名的严格解，再到三维模型严格解依然是世纪难题，都是磁学和统计物理学知名的历史故事。然而，实际晶体中，给一维和二维磁体定义 Ising 自旋，未必合理，因为那各向异性无穷大的两重态缺乏微观物理来源：一个单层的磁性原子层，靠什么能够约束其自旋只能上下两重态？自旋轨道耦合好像不够。因此，严格满足二维 Ising 模型的体系不大可能存在。

另外一个极端，就是各向同性的海森堡二维自旋体系，成就了那个著名的 Mermin – Wagner (MW) 定理：各向同性的海森堡磁性二维体系没有长程序。这一定理让多少物理人意兴阑珊、收兵回朝，不再深入探讨二维磁性问题，直到近来被接近真实的二维磁体具有长程序的实验所惊诧。今天的二维磁性正方兴未艾，当然并非 MW 定理的错，而是因为真实的二维磁体未必就是单纯一层磁性原子排列而成。那些二维材料，其晶格单元依然存在面外结构，第三维特征依然存在，依然可以施加磁晶各向异性。再加上目前的实验样品在 xy 平面的尺度有限，边缘效应也可能导致磁性异常。Ising 不懂二维磁性，只是借助道听途说而了解了一些磁性维度效应的复杂性。

(3) 铁电：铁电物理中维度效应也很重要，导致铁电体维度的研究比磁性材料人去关注维度的历史还要久远。从退极化这一简单图像去预言铁电尺寸效应，言之灼灼、语之戳戳，都是 1990 年代之前的事情了。一些成果还被明明白白写在诸如钟维烈老师的《铁电物理学》著作中。铁电体的维度效应，一直是铁电物理的前沿，也与现代集成铁电技术发展密切相关。不过，过去几十年，铁电物理人将这个尺寸和维度极限不断地推向底层，包括纳米线、单个晶胞厚度的薄膜、撕扯出来的 vdW 二维材料。也不知道是该高兴还是该失望，这个铁电尺寸效应并不明显，更不要说预言的铁电维度极限正在不断被压缩。这些结果，将经典教科书中铁电尺寸效应的那几页物理戳得千疮百孔，也可见铁电维度效应的复杂性。

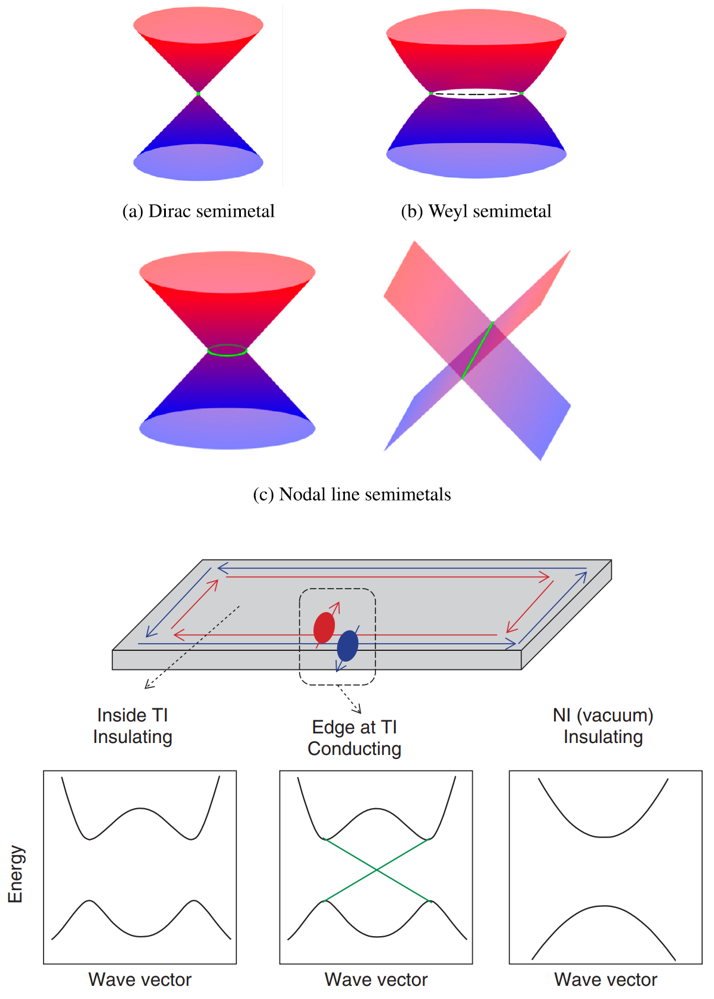
图 2. 拓扑量子材料中维度的对应关系 (无需详细解读)。

上图来自：S. Y. Yang et al, Symmetrydemanded topological nodal line materials, Adv. Phys. X3, 1414631 (2018), https://doi.org/10.1080/23746149.2017.1414631

下图来自：https://www.ntt-review.jp/archive/ntttechnical.php?contents=ntr201707fa6.html

这些具有历史韵味的实例告诉我们，维度可以影响介观微结构、影响对称性、影响相变，OK，及至影响一切。但这些例子也告诉我们一些简单的事实：理论预言的、理想化约束条件下的维度物理，在实际材料中未必满足。个中差池，就给了低维物理突出重围、产生新效应和新应用的机会，体现了现实总是在理想化的极端之间取道“中庸”的事实。也许物理本来就是如此，只是需要我们去“知其然并知其所以然”，以此发现和利用之、并企图造福人类。

这种认识的后果，就是今天物理人对低维凝聚态和低维量子材料的广泛研究，包括那些热点实例，如碳 60、碳纳米管、石墨烯，如 vdW 二维材料、魔角二维材料，如界面二维电子气、量子阱等。其中，对当下的拓扑量子材料，维度显得更为别致和新奇，如图  2 所示。不知道小编 的如下理解是不是算胡诌：

(1) 非磁性拓扑绝缘体，因为费米面附近的拓扑非平庸能带结构，存在体 - 面对应性，即三维绝缘体态对应二维表面金属态。

(2) 磁性拓扑绝缘体，因为费米面附近的拓扑非平庸能带结构和磁性，存在体 - 边对应性，即三维绝缘体对应二维表面能隙和一维自旋极化的边缘金属态。

(3) Weyl 半金属，也因为费米面附近的拓扑非平庸能带结构，存在三维半金属态、二维表面费米弧和零维的“磁单极点”。

所以，我们看到了，拓扑量子材料中那些维度的表象显得更加突出，因为动不动就是整数维度的量子材料新效应，如三维绝缘体、二维金属、二维费米弧、一维金属、零维 Weyl 点 (磁单极子)。好吧，物理人说还远不止于此，当下那些 cutting – edge 问题包括费米面附近出现的那些零维的节点 (nodal point)、一维的节线 (nodal line)、二维的节面 (nodalsurface)。

维度，在这里就是一张无形而有实的大手，“掌控”着量子材料、拓扑量子材料。

有意思的是，这些拓扑量子材料的低维性质，似乎绝大多数附属于三维体态。诸如碳纳米管和石墨烯这样“真正的”、“独立自主的”一维和二维拓扑量子材料并不多见，至少如石墨烯这般知名的低维拓扑材料不多。不过，过去一些年，二维材料不断发展，二维量子材料家族也很兴旺。如此，必然催动物理人走向更底层：那，有没有真实的、独立自主的一维量子材料？甚至是一维拓扑量子材料？

挺好的问题！要说凝聚态物理和量子材料中有什么重要的问题无人问津，那倒极为困难。通过各种微纳制备技术，已经获得的一维、准一维量子材料很多，研究历史也不短。例如，在固体表面生长一些纳米线总是可以的，或者通过其它技术手段“制造”出一维、准一维结构，也不是难题。过去这些年，利用有机材料独特的分子结构设计和合成技术，制备一维有机量子材料的机会要大一些，包括电荷密度波、Peierls 相变、孤波、自旋 - 电荷分离以及那个著名的 Su – Schrieffer – Heeger(SSH) 理论预言的能带拓扑态等，也多有见诸报道。

但是，到目前为止，一维无机多元复杂化合物量子材料，包括一维无机拓扑材料的“制造”，大概不容易。若要说容易，那必然是新颖别致和值得推崇的！

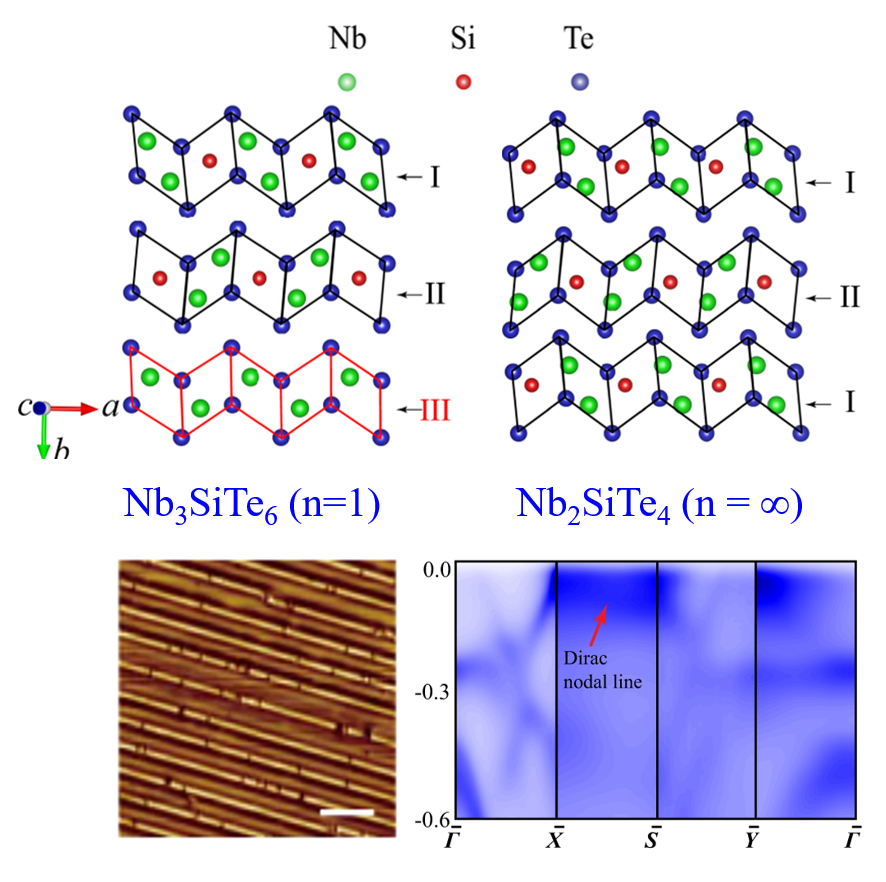
图 3. 柳仲楷和陈宇林老师他们关注的体系：NbSixTe2 (x = 0.33 to 0.5) 或 Nb2n+1SinTe4n+2 (n = 1,2,…,  ∞)：结构、样品表面一维链的实物形貌及能带中清晰的 Dirac nodal line。

最近，上海科技大学的柳仲楷和陈宇林老师他们，联合南京大学、新加坡科技设计大学、劳伦斯伯克利实验室和清华大学的同行们合作，就在一维拓扑量子材料问题上迈出了一“小”步。这里的“小”，是走向底层的“小”。他们将一些结果整理后，发表在《npj QM》上，让 小编有机会学习和领会他们的工作，并写几句粗浅的学习心得。

陈宇林和柳仲楷老师他们都是 ARPES 的行家，一定是做梦都想利用这一有力工具去探测那些一维量子材料能带结构和拓扑量子新效应。不过，ARPES 的探测技术原理注定了样品不能是一根孤零零的一维链，必须是足够多的、且有序地排列的一维链集合体！这种情形很像中子散射实验。针对单一的二维或一维材料的中子散射，到今天依然是巨大挑战：样品要有足够的体量！

问题是，这样的机会太小了。问题更是，这样的机会他们有意地“碰”上了！

最近一些年，已经有量子材料人关注那些组成可调控的无机化合物，如 NbSixTe2 (x = 0.33 to 0.5) 或 Nb2n+1SinTe4n+2 (n = 1, 2,…,  ∞)，它们在结构上天然就能形成有序排列的准一维 NbTe2 链。通过调控组分 x 或 n，这一有序排列的链状结构间距可以变化，从而有可能获得从一维到二维连续可调的量子材料体系。

更因为，这种一维链状结构可以整齐划一地定向有序排列，堆砌于整个三维晶体中，给 ARPES 探测这些一维链提供了现实的可行性。而且，如上所述，调节组分 x，让这些一维链相互靠近，实现从一维走向二维、甚至三维链束的过渡成为可能。

陈老师和柳老师他们团队，似乎就这样“轻而易举”地搞定了研究对象。接下来，这些一维链就是他们的“刀下鱼肉”，听凭其“宰割”了。

这篇文章主要展示了如此精巧的准一维结构 (metallic NbTe2 chains) 的电子结构特征，特别是其非平庸拓扑特性。得到的主要结论是：能带费米面附近的狄拉克半金属态，乃是具有节线的狄拉克态 (Dirac nodal line structure)，受晶体与时间反演对称保护。这样一个节线狄拉克半金属体系，通过适当结构调控和磁性掺杂，有可能得到 Weyl 半金属及新颖的拓扑边缘态。通过增加 NbTe2 一维链的密度 (减小其间距)，ARPES 也清楚展示了能带结构及其拓扑特征从一维向二维的转变，如图 4 所示。整个文章的故事新颖、物理图像清晰明了。

拓扑量子物理的关注点，主要是动量空间中能带结构的维度花样。本文所展示的拓扑量子维度效应，关注点则正走向实空间的维度花样。这是量子材料人科研生命中必然的元素及张力，也给了凝聚态物理以更丰富的维度与形态。虽然这些花样能不能最终走向为人所用尚未有答案，但可控制造实空间可组装的不同维度体系、并赋予其拓扑量子功能，是引领性的一步。阿门！

当然，柳、陈团队针对的一维 NbTe2 一维链，却还是依附于 Nb2n+1SinTe4n+2 晶体内部的，距离“真正的”、“独立自主的”一维体系，还是差那么一点！

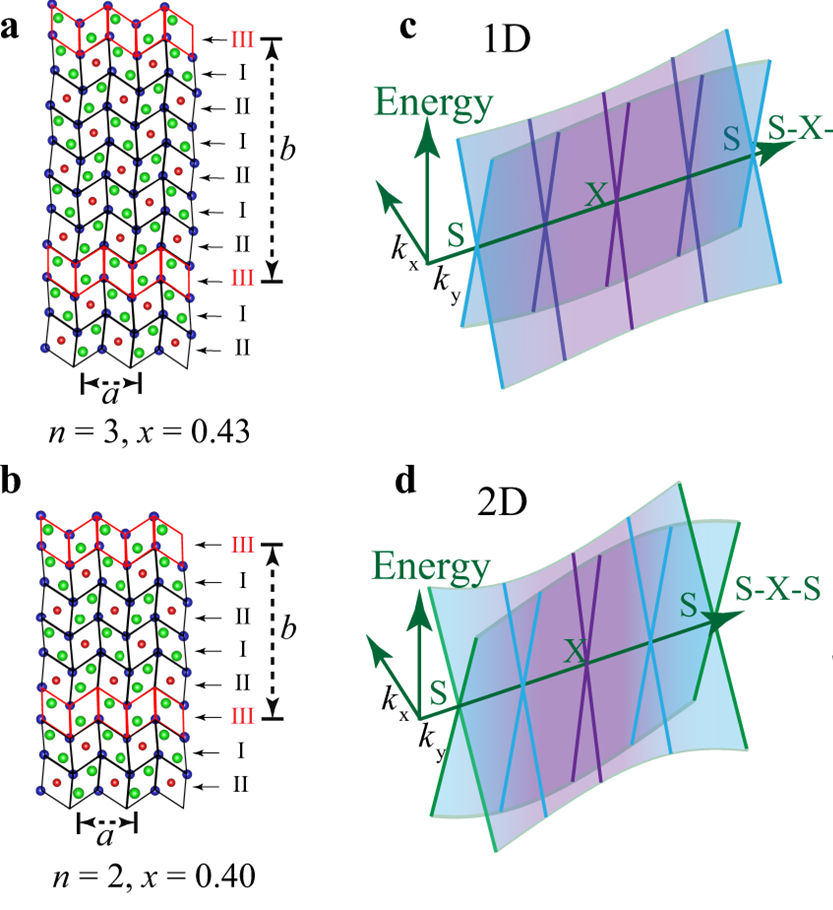
图 4. 随着 x 或者 n 的变化，Nb2n+1SinTe4n+2 体系从 1D 走向 2D 的过程，对应的拓扑量子态也发生演化。

审核编辑 ：李倩