关于贝叶斯定理的几个概率定义

1 贝叶斯定理

1.1 几个概率定义

先验概率(边缘概率)：某个事件发生的概率，通常是在没有条件约束下事物的客观发生概率，比如抛硬币的50%概率

后验概率(条件概率)：一个事件在另一个事件已经发生的条件下的发生概率

1.2 条件概率公式和全概率公式

条件概率公式：

全概率公式：

1.3 贝叶斯公式

贝叶斯公式可以简单的通过条件概率公式和全概率公式推出：

可以简写成：

2 贝叶斯定理的含义

我们可以将贝叶斯公式写成：

其中，P(A)为事件A发生的先验概率，为事件A发生的后验概率，称为似然函数，它可以看作一个调整因子，它通过对先验概率进行调整，使其更加接近真实概率。

故贝叶斯公式可以理解为：

后验概率 = 先验概率  似然函数

贝叶斯定理的含义也就是：为了估测一个事件A的真实概率，我们对该事件加入一个实验结果，即似然函数，当似然函数大于1，则先验概率被增强，A事件发生可能性变大：当似然函数小于1，则先验概率被削弱，A事件发生可能性变小。

3 一个例子

eg.已知某种疾病的发病率为0.001，即1000个人中会有1个人得病。现有一种试剂可以检测患者是否得病，它的准确率为0.99，即在患者得病的情况下，它有0.99的可能性呈阳性。它的误报率为5%，即患者在没有得病的情况下，它也会有5%的可能性呈阳性。现有一个病人的检验结果为阳性，请问他确实得病的可能性有多大？

解：定义事件A为患者得病，事件B为检验结果阳性。
所以我们要计算的为。
利用贝叶斯公式：

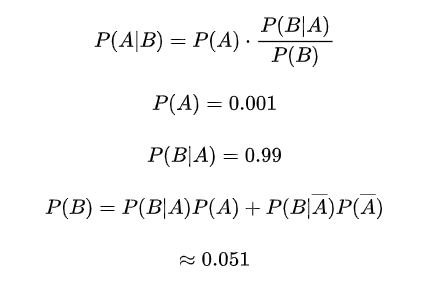
可知，检查结果为阳性患病可能性也并不大，即“假阳性”。

审核编辑 ：李倩