陀螺仪的基础知识和结构

陀螺仪是一种测量物体旋转速度的传感器。陀螺仪的工作原理对许多工程师来说可能是神秘的。

考虑到这一点，并且受到 来自 Analog Devices 的一篇文章的启发，本文试图对MEMS振动陀螺仪背后的理论进行更详细的解释。由于全面的分析可能涉及数学密集型，我们将尝试考虑传感器的特殊方向，以尽可能简化讨论。

使用极坐标系定位旋转对象

使用极坐标系可以更容易地描述旋转物体的位置。假设，如下图 1 所示，对象始终位于 XY 平面内。

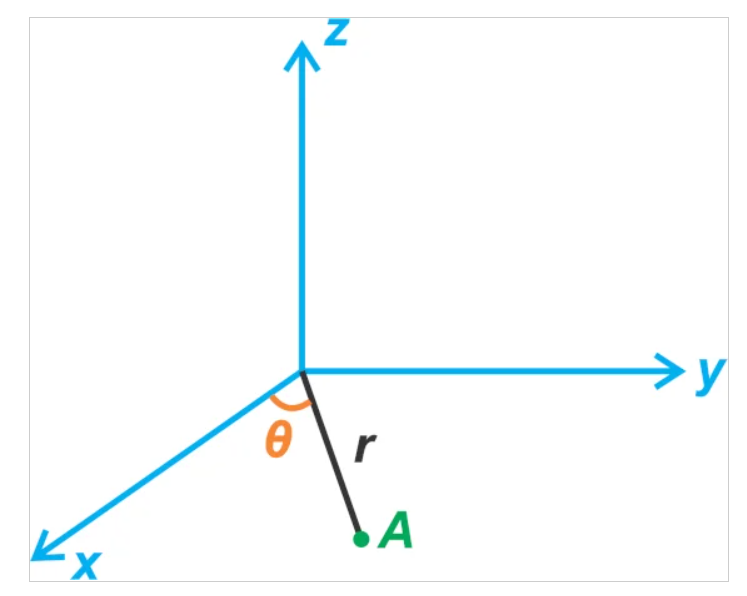
图 1. XYZ 平面上的示例对象。

随着 θ 的变化，点 A 围绕 z 轴旋转。您可能记得在数学课中，单位向量 ^rr^ 和 ^θθ^ 是为极坐标系定义的，如图 2 所示，以唯一地指定坐标系中的一个点XY 平面。

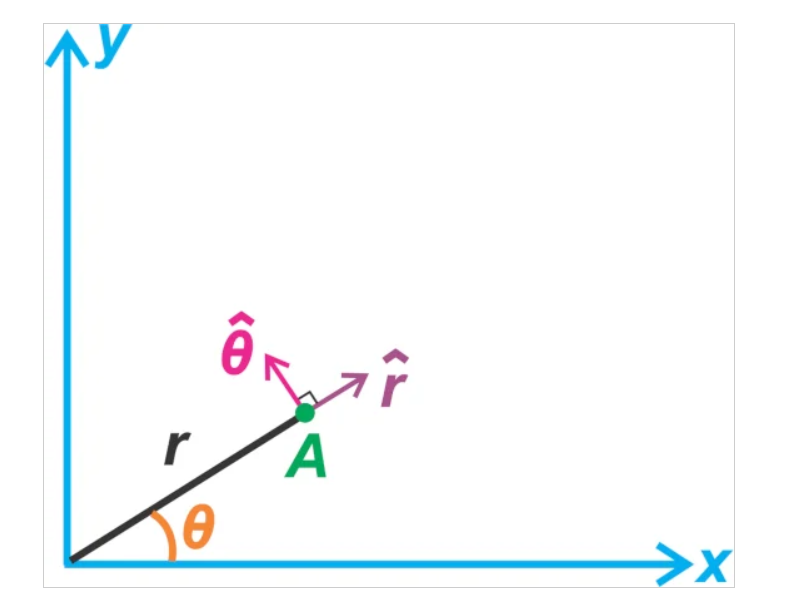
图 2. 极坐标系示例。

第一项考虑了一个明显的点：如果我们保持 θ 不变，我们仍然可以通过将物体与原点的距离改变 Δr 来改变物体的位置，如图 3 所示。在这种情况下，速度应该具有径向分量，即在$$\hat{r}$$的方向。^rr^.

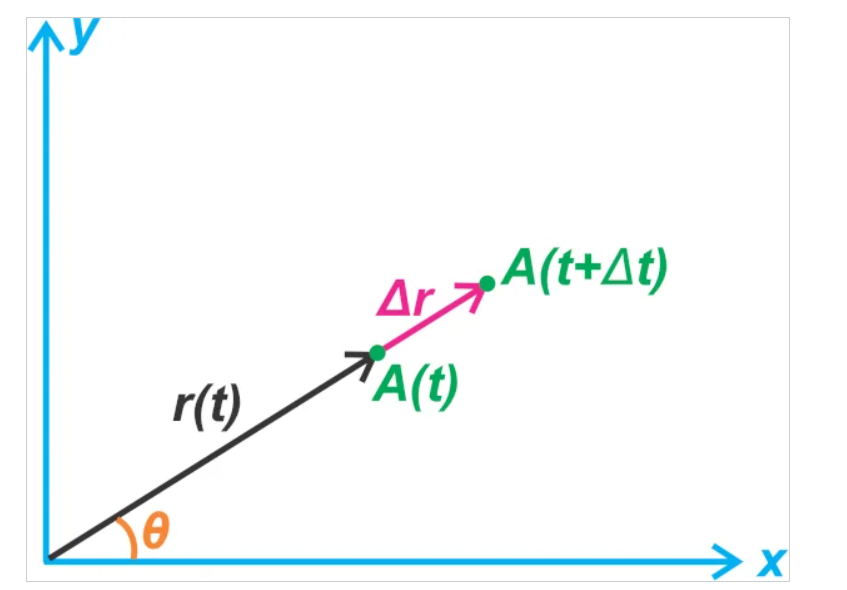
图 3. 通过改变距离来改变物体的位置。

等式 2 中的第二项考虑了这样一个事实：即使与原点的距离是恒定的，物体的位置也会因旋转而改变。请记住，尽管 $$\hat{r}$$ 的长度为 1，但它的方向取决于 θ 并且可以随时间变化。图 4（a） 显示了如果我们保持 r 不变并将角度增加 Δθ，则位置如何变化。^rr^长度为 1，它的方向取决于 θ 并且可以随时间变化。图 4（a） 显示了如果我们保持 r 不变并将角度增加 Δθ，则位置如何变化。

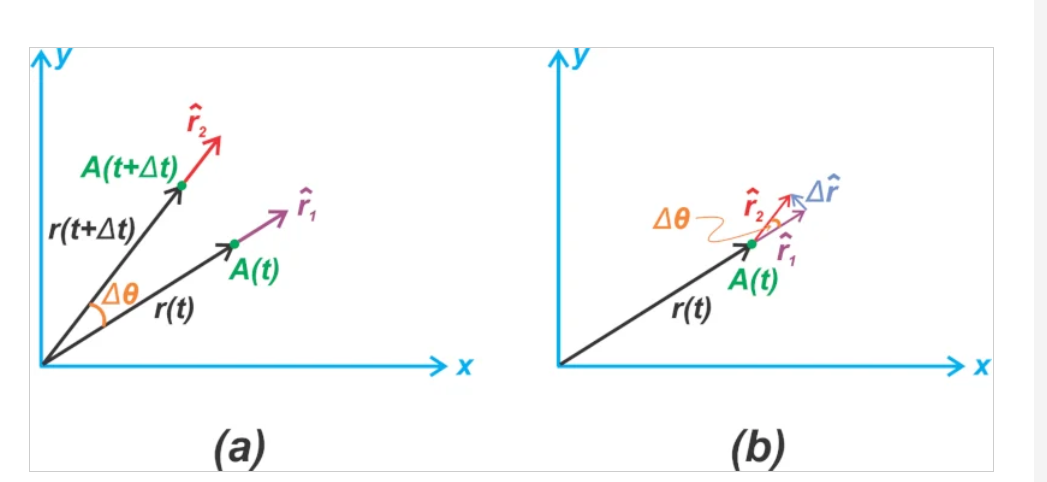
图 4. 如果 r 为常数且角度增加 Δθ （a） 并找到该变化 （b） 时位置如何变化的示例。

VA→=drdtr^+rdθdtθ^

洞察方程式

等式 8 中的切线项是振动陀螺仪运行的关键。让我们更仔细地研究一下这个术语是如何创建的。图 5 显示了珠子沿旋转轮辐移动的轨迹。

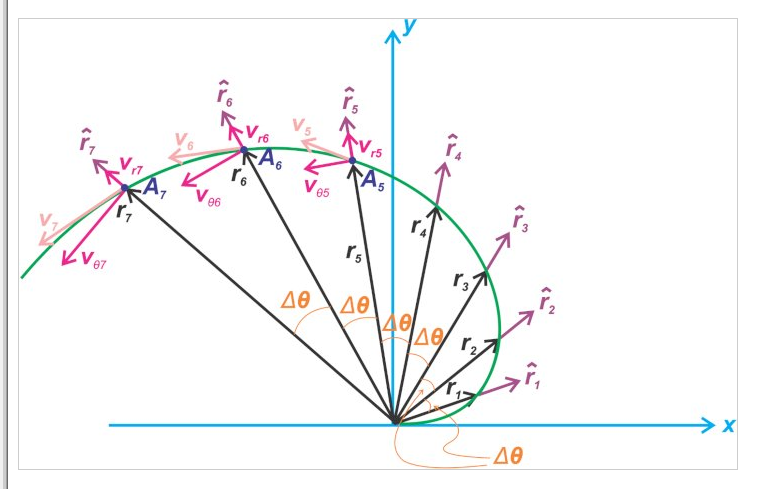
图 5. 显示珠沿旋转轮辐轨迹的示例。

vθ=rdθd吨=rωvθ=rdθdt=rω

图 5 显示了位置 A5、A6 和 A7 的这些速度分量。在我们的示例中，径向分量的大小是恒定的，但是切向分量呢？

由于 ⍵ 是常数，因此速度的切向分量随 r 增加。换句话说，当我们远离原点时，珠子必须在给定的时间间隔和 Δθ 内移动更长的距离。通过比较连续位置向量之间的距离，您可以清楚地看到这一点。

另一个问题是由于这种现象，切向速度的变化速度有多快？

对于给定的 ⍵，给出加速度的切向分量的切向速度的变化率等于 r 的变化率。因此，切向加速度的一个分量由下式给出：

MEMS陀螺仪的基本结构

图 6 显示了振动陀螺仪的基本结构。

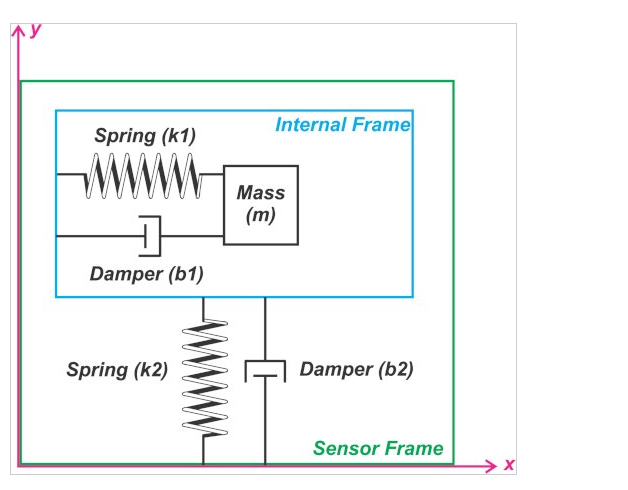
图 6. 振动陀螺仪的示例结构。

质量 （m） 通过阻尼弹簧结构连接到“内部框架”。此外，由正反馈系统（上面未显示）控制的致动器用于驱动质量进入谐波振荡。如图所示，反馈系统保证质量保持在沿 x 轴的可调节连续振荡中。此外，内部框架通过相对于质量振荡方向呈 90° 的第二阻尼弹簧结构连接到“传感器框架”。当在该方向上存在力时，这种配置允许内部框架能够在 y 轴方向上移动。

正如我们将在下一节中看到的，当传感器绕垂直于图中所示 XY 平面的轴旋转时，图 6 所示的结构可以检测角速度。

振动陀螺仪如何工作？

假设，如图 7 所示，陀螺仪固定在逆时针方向旋转的平台上。

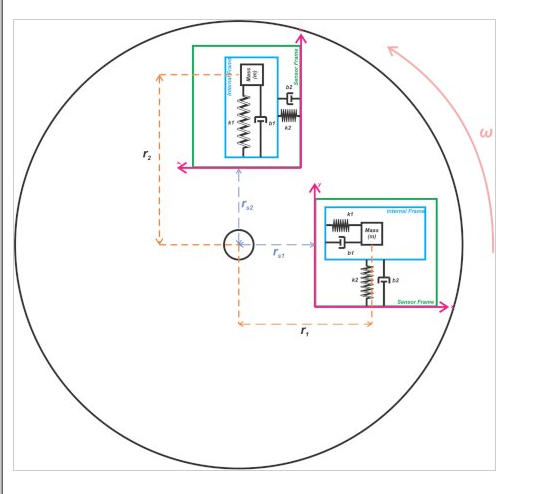
图 7. 固定平台上逆时针旋转的陀螺仪。

该图显示了两个不同时刻的传感器。尽管传感器封装与平台中心的距离是固定的，但我们知道质量距离从 r 1变为 r 2是由于其在传感器框架的 x 方向上的振荡。在此示例中，质量距离增加 r 2 》 r 1。

与图 5 中描述的磁珠示例类似，检测质量在传感器 y 轴的正方向上经历切向加速度。在 y 方向上，质量块刚性连接到内部框架。因此，同样的加速度也适用于内部框架。内部框架；然而，最初倾向于保持静止，这会改变内部框架相对于传感器框架的相对位置。