三种高速乘法器实现原理

摘要：乘法是数字信号处理中重要的基本运算，在很大程度上影响着系统的性能。本文将介绍三种高速乘法器实现原理：阵列乘法器、华莱士（WT）乘法器、布斯华莱士树超前进位乘法器。而且通过FPGA技术实现了这三种乘法器，并对基于以上三种架构的乘法器性能进行了分析比较。

关键字：阵列乘法器，华莱士乘法器，超前进位乘法器，FPGA

引言

随着3G技术的发展，关于图像、语音、加密等数字信号处理技术随处可见，而且信号处理的实时性也要求越高。实时性即是要求对信号处理的速度要快，而乘法器是数字信号处理中重要的基本运算，在很大程度上影响着系统的性能。人们开始开发高速的乘法器。

以下将对三种乘法器：阵列乘法器、华莱士（WT）乘法器、布斯华莱士树超前进位乘法器进行原理分析，并用FPGA技术实现了这三种乘法器，对其结果进行了仿真，得出相应的性能比较。

阵列乘法器

2.1 阵列乘法器原理

硬件乘法器的常规设计是适用“串行移位”和“并行加法”相结合的方法，这种方法并不需要很多器件。然而串行方法毕竟太慢，执行一次乘法的时间至少是执行一次加法时间的n倍，不能满足科学技术对高速乘法所提出的要求。自从大规模集成电路问世以来，高速的单元阵列乘法器应运而生，出现了各种形式的流水线阵列乘法器，它们属于并行乘法器，提供了极快的速度。阵列乘法器的运算过程如下：

第一：当乘数的位数字为1 时，我们可以将被乘数的值直接放置适当的位置。而适当的位置是依乘数的第几个位和被乘数做运算之后所放的位置。

第二：当乘数的位数字为0 时，我们可以将0 放置适当的位置， 以作为部分乘积。

第三：我们利用笔和纸计算的乘法，在硬件中使用与门来实现。例如：1000 ×1中，乘数1 和每一个被乘数的位都个别做与运算，其结果为1000 正是我们所要的结果。由此可知我们只需用与门就可以完成我们所要的乘法。

第四：当部分乘积都运算完成后，使用加法来完成最终的乘法结果运算。

根据以上四点的说明，我们可以运用最简单、最直观的方式来描述固定点乘法器的电路描述。我们使用与门来做部分积运算，使用全加器（Full adder）来运算部分积的最终结果。图1所示为有符号位的6×6固定点乘法器的架构图。

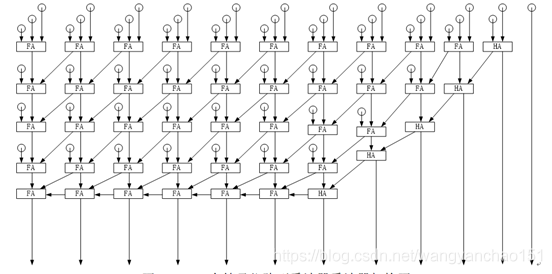
图1 6×6有符号位阵列乘法器乘法器架构图

2.2 阵列乘法器FPGA仿真

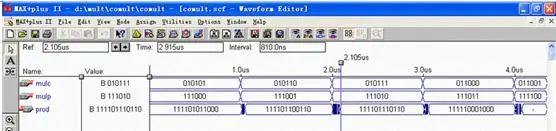
在名为comult的实体中设置mulc和mulp两个输入端口和一个prod输出端口。其中mulc代表被乘数，mulp为乘数，二者均为6位。乘积prod是一个12位的结果，输入与输出端口的数据类型均为std_logic_vector。流程图如图2所示，仿真如图3所示。

图2 6x6有符号阵列乘法器流程图

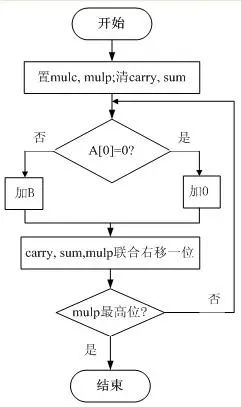
图3 6x6有符号阵列乘法器仿真

华莱士乘法器原理

部分积相加， 若采用累加移位的方法， 速度太慢。华莱士树算法（Wallace Tree Algorithm）是部分积化简的一种树形算法。它使乘法器的延时得到最大限度的缩短，但全加阵列的布局布线复杂度大为增加。

一个全加器有三个输入： A ， B ， C （进位） 和两个输出S ， C′（输出进位） ， 3个输入对2个输出而言是对称的， 即它们互相交换位置， 结果不会受影响。如果把一串全加器简单排成一行， 它们之间进位线不连， 把这样一串全加器称为保留进位加法器（CSA ） ， 它有以下特性： 三个输入数之和等于二个输出数之和， 即3个相加数每通过一次保留进位加法器， 其个数就减少1个。

Wallace最早提出的方案就利用了这一特点：第一步将每列的部分积按三位进行分组，每组通过使用全加器构成的CSA部件，将加数的数目减少;第二步对第一步产生的结果仍按三位分组的方式将同权的伪和与局部进位信号通过CSA 部件进行处理，再次减少加数的数目，这种处理一直进行到最后只有两个输出为止。对最后的伪和与局部进位通过进位传递加法器相加得出真正的结果。在这种处理方式中，每列中求伪和的操作是并行完成的。由于采用全加器作为加法部件，每次能将3个权为20的输入信号经处理后得到一个权为21的局部进位信号和一个权为20的伪和信号，这样操作数的数目减少1/ 3，将产生的中间伪和也按照这种方式处理，经过时间为O（log3/ 2 N） 的处理后可以得到最后的伪和与局部进位信号。

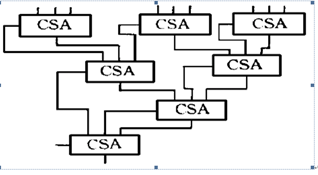
图16 华莱士树加法树示意图

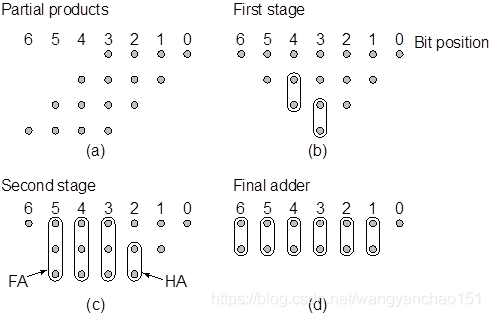
图17 4x4位华莱士树乘法器实现图

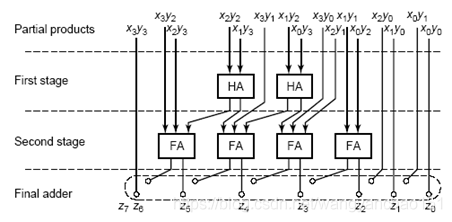
图18 4x4位华莱士树乘法器架构图

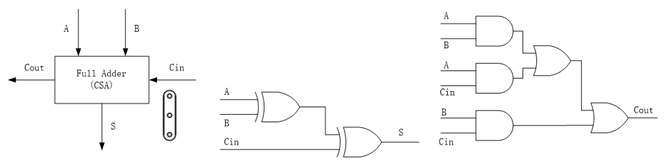
图19 保留进位加法器（CSA）

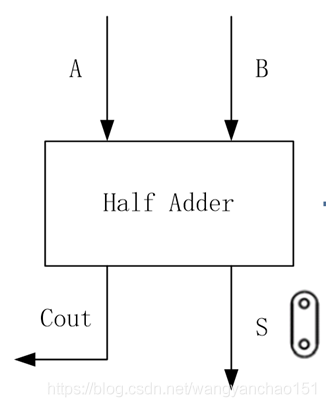
图20 半加器

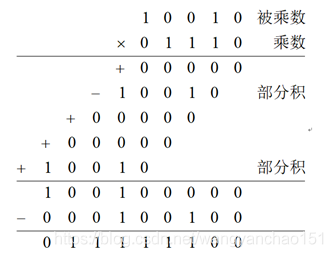
布斯算法（Booth’s Algorithm）的做法是对乘数编码以计算出乘法运算的结果，主要的想法在于乘数中连续的1，这些1会造成被乘数的连加。

但是，乘数01110又可表示为10000-00010，这样可将部分积减少为2个。当我们遇到乘数中连续的’1’时（从右往左看），第一个’1’减去被乘数，最后一个’1’后面的’0’则加上被乘数。

布斯编码的核心在于对连续的’1’字串进行头、中、尾三段的分段处理（从右往左看）。当然，’0’字串由于本身就无须进行运算，所以不必理会。

华莱士乘法器

先介绍阵列乘法器，我们用笔计算乘法时，第一个操作数为被乘数（multiplicand），第二个操作数为乘数（multiplier）。而乘数中的每一个位和被乘数做相乘的运算后的结果称之为部分乘积（partial product），而将所有的部分乘积相加之后，其运算结果称为乘积（product）。如：1000×1001为例，

通过以上的示例我们可以发现如下四点：

第一：当乘数的位数字为1 时，我们可以将被乘数的值直接放置适当的位置。而适当的位置是依乘数的第几个位和被乘数做运算之后所放的位置。

第二：当乘数的位数字为0 时，我们可以将0 放置适当的位置， 以作为部分乘积。

第三：我们利用笔和纸计算的乘法，在硬件中使用与门来实现。例如：1000 ×1中，乘数1 和每一个被乘数的位都个别做与运算，其结果为1000 正是我们所要的结果。由此可知我们只需用与门就可以完成我们所要的乘法。

第四：当部分乘积都运算完成后，使用加法来完成最终的乘法结果运算。

根据以上四点的说明，我们可以运用最简单、最直观的方式来描述固定点乘法器的电路描述。我们使用与门来做部分积运算，使用全加器（Full adder）来运算部分积的最终结果。因为作加法时，会有进位问题，且上一位所产生的进位也非常重要，所以只有全加器能满足我们的加法要求。图13所示为有符号位的6×6固定点乘法器的架构图。

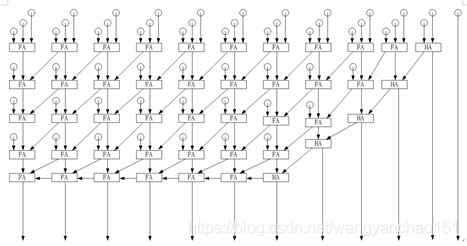
图13 6×6固定点乘法器架构图

原文标题：三种高速乘法器的FPGA实现及性能比较

文章出处：【微信公众号：FPGA设计论坛】欢迎添加关注！文章转载请注明出处。　　

      审核编辑：彭静