光度学的几个基本概念

与“光"和"影像”打交道的同学，光度学的这几个基本概念还是要了解和熟悉的。   光度学  以人眼为基础   在可见光波段内，考虑到人眼的主观因素后的相应计量学科称为光度学。光度学是1760年由朗伯建立的，定义了光通量、发光强度、照度、亮度等主要光学光度学参量，并用数学阐明了它们之间的关系和光度学几个重要定律，如照度的叠加性定律、距离平方比定律、照度的余弦定律等，这些定律一直沿用至今，实践已证明是正确的。光度学除了要定义一些物理量并确定相应的测量单位外，还要研究测量仪器的设计、制造和测量方法。

流明、勒克斯、坎德拉、坎德拉每平方米这4个单位属于光度学（Photometry）的概念，与辐射度量学（Radiometry）概念可以一一对应进行理解。其差别在于：

Photometry（光度学):基于的是“眼睛，人的感觉” Radiometry（辐射度量学):基于的是“实际物理能量”  

光通量  光度学中的“功率”

光通量的单位是“流明”，1流明lm是发光强度为1cd的均匀点光源在1球面度立体角内发射的光通量，是光度学上类比于“功率”的概念，和辐射度量学上的瓦特（W）是可以进行对应并进行理解的。

在光度学中，光通量明确的被定义为能够被人的视觉系统所感受到的那部分光辐射功率的大小的度量。

在人眼最灵敏的555nm处，流明(lm)和瓦特（W）的换算关系常数Km=683lm/W(明视觉）。或者说，真实的功率（Φe）为1W的555nm的光，其光通量（Φ）为683流明。

而对于其他波长l，由于人眼不那么灵敏，同样功率为1W的光，其光通量（Φ）是达不到683lm的；或者说同样1W的光，我们会觉得其他颜色的光不及555nm的亮，ν（λ）越小，我们会觉得这光越弱。对于任意波长λ，如果其功率是Φe(λ)，那么在光度学上的光通量（Φ(λ)）为：Φv（λ）=KmV（λ）Φe（λ）

光谱光视函数V（λ）（即视见函数，见可见光）如下图：

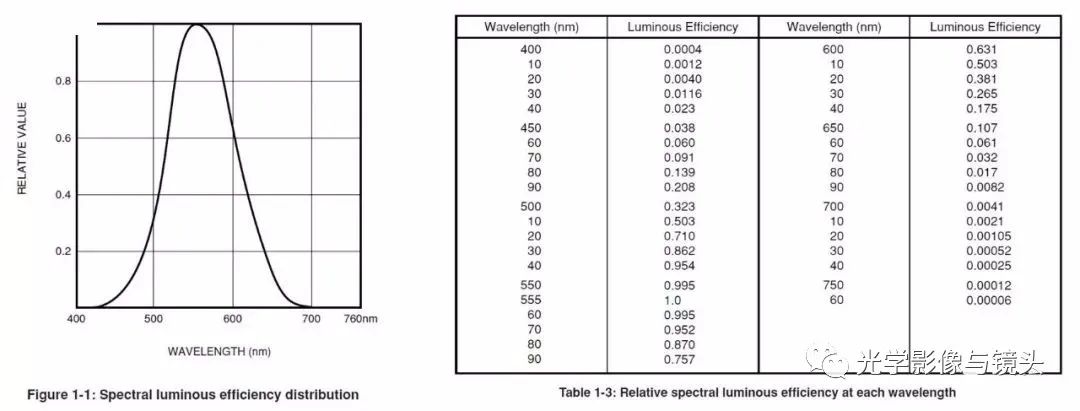
复色光的光通量需对所有频率的光通量求和，需要将所有波长都考虑进来，所以在“功率”这个概念中，辐射测量学中的“功率/瓦特”和光度学中的“光通量/流明”可以如下换算：

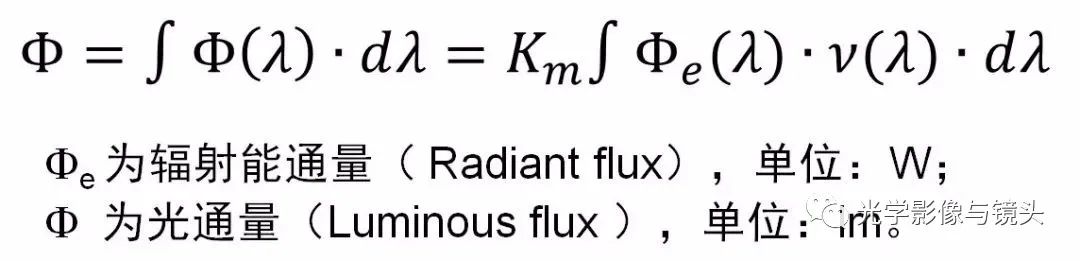
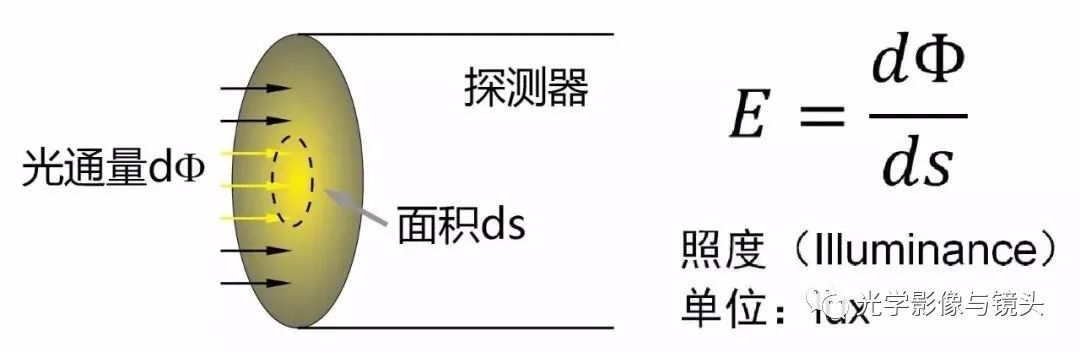
照度  物体/探测器受到了多少功率

勒克斯（lux）这个单位以及其对应的概念照度（illuminance），用于描述单位面积的物体/探测器受到了多少“功率”（光通量）；通俗的说，其描述的是“被照”得厉不厉害。其在辐射测量学上对应的单位是：W/m2。

照度这个概念（单位lux），以及对应的辐射度量学概念辐射照度（单位W/m2）对于光探测器件的对比与评价非常重要。

发光强度  人眼看来点光源的亮度究竟如何

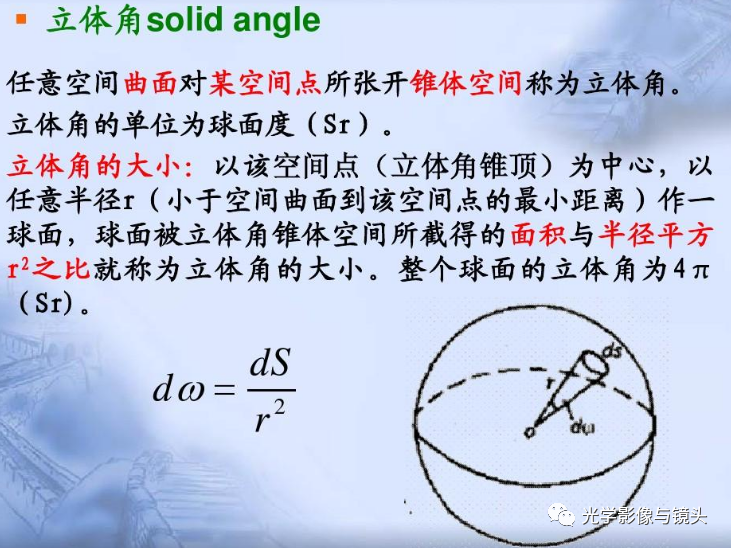
坎德拉（cd）这个单位以及其对应的概念发光强度（Luminous intensity），被用于描述在人眼看来，一个点光源究竟亮不亮，以点光源为原点的单位立体角（单位为球面度sr）内总共有多大的“功率”。其在辐射测量学上对应的单位是：W/sr（瓦特每球面度）。

坎德拉（cd）与极为常用的米、千克同样贵为7个国际基本计量单位之一。

坎德拉及对应的概念发光强度是对光源本身的描述，与被照物、光学系统都没有关系。

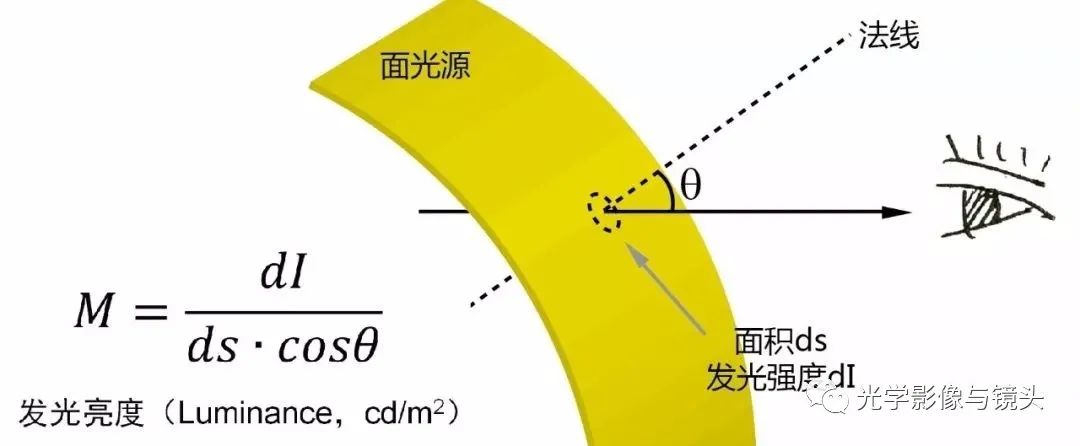
发光亮度 人眼看来面光源的亮度究竟如何

除了点光源，面光源也非常常见。所以另有一个发光亮度的概念来描述面光源的强度。而对于面光源，观察者和这个面所呈的角度也很重要，所以在发光强度的基础上除了需要考虑面积，还得考虑面与观察者的角度问题。

特别的，在LED显示屏领域有一个常见单位尼特（nit），一些笔记本电脑的显示屏会给出其发光亮度数值（如300nit），这个单位和cd/m2实际是一回事儿。

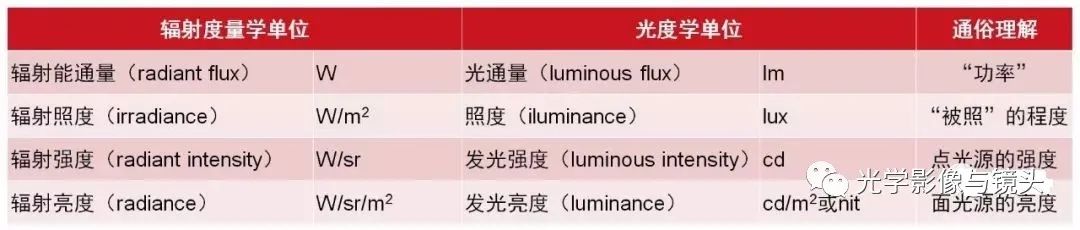
以上是关于光度学中四个重要单位的简单介绍啦，希望对大家的理解有所帮助。最后，就用一张表，对辐射度量学与光度学几个基本概念进行对比，让同学们更加好理解。

审核编辑 ：李倩