

高速移动下OFDM均衡器的FPGA实现
FPGA/ASIC技术
描述
0 引言
正交频分复用(OFDM)是一种正交多载波调制技术,它将宽带频率选择性衰落信道转换成一系列窄带平坦衰落信道,在克服信道多径衰落所引起的码间干扰,实现高数据传输等方面具有独特的优势。但是由于OFDM信号频谱重叠,对信道变化很敏感,在高速移动下,信道的时变特性更加明显,此时OFDM系统载波间的正交性会遭到破坏,出现载波间干扰(ICI),这会导致系统性能明显降低。为了消除ICI,必须采用适当的均衡技术以补偿ICI。国内外许多学者对这些问题进行了大量的研究,提出了各种不同的方法,得到了一些阶段性成果。文献提出了一种低复杂度的迭代MMSE均衡器算法,在保证均衡效果的同时把运算量成功降低到o(N),为该均衡器算法的实际运用奠定了基础。
现场可编程门阵列(Field Programmable Gate Array,FPGA)器件近年来取得了飞速的发展,已经具有强大的计算性能和逻辑实现能力。特别是Xilinx公司的FPGA具有丰富的IP资源,容量大且具有强大的软件支持,在各个领域得到了广泛的应用。本文主要讨论基于Xilinx公司Virtex-2 FPGA硬件平台的均衡器算法中矩阵求逆的运算过程实现。将程序下载到FPGA,并通过RS 232将结果数据回送到主机查看和验证。
1 时变信道中OFDM系统均衡器
1.1 时变信道中的OFDM系统结构
考虑一个载波数为N的OFDM系统如图1所示,假设完全同步,并且有足够长(不小于信道阶数)的循环前缀(CP)。在去除了循环前缀CP以后第i个数据帧收到的数据矢量为:
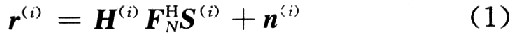
式中: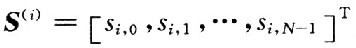 OFDM第i个数据帧的输出数据矢量;
OFDM第i个数据帧的输出数据矢量;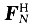 为N点快速傅里叶逆变换矩阵;,n(i)为信道噪声矢量,定义方差是σ2的高斯白噪声(AWGN);H(i)是一个N×N的时域转移矩阵,其元素为
为N点快速傅里叶逆变换矩阵;,n(i)为信道噪声矢量,定义方差是σ2的高斯白噪声(AWGN);H(i)是一个N×N的时域转移矩阵,其元素为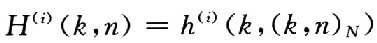 ,其中h(i)(k,n)是描述信道特性的冲击响应。在接收端,对r(i)进行N点快速傅里叶变换,其输出为:
,其中h(i)(k,n)是描述信道特性的冲击响应。在接收端,对r(i)进行N点快速傅里叶变换,其输出为:
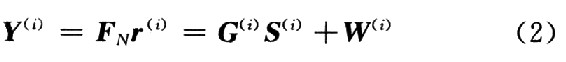
式中: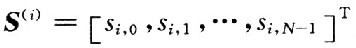
由于在高速移动的环境下,接收信号会受到ICI的影响,故在整个系统中添加均衡模块,假设均衡器用E(i)来表示,则均衡后的信号可以表示为:

1.2 MMSE均衡器算法
把上面式中的i去掉,根据最小均方误差的规则,可以简写得到均衡矩阵为:
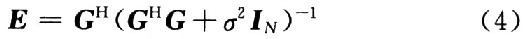
在时变信道中,G不是对角矩阵,则矩阵求逆的直接算法的运算量为o(N3),利用文献给出的结论:ICI主要来自相邻的几个子载波,并且每个子载波的符号能量主要泄漏至邻近的少数子载波上,也就是说,G中的很大一部分元素是可以忽略的。然后再采用迭代的方法对矩阵求逆,把运算量降为o(N2),但是在实际应用中,N是一个较大的数值,这个方法计算量仍然很大,所以很多算法在考虑均衡效果的同时也尽量减少运算量,以增强算法的可实现性和最终均衡的实时性。
根据Chen等验证得到G可以被进一步简化成如下Ak来描述:
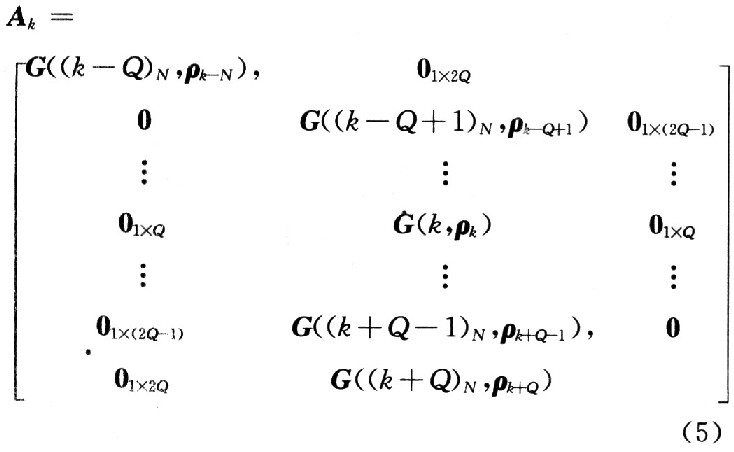
式中:pn是一个由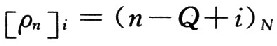 构成的1×(2Q+1)的矩阵,i=O,1,…,2Q。MMSE均衡器可以描述为
构成的1×(2Q+1)的矩阵,i=O,1,…,2Q。MMSE均衡器可以描述为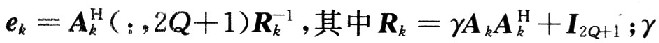 ;γ为该信道的信噪比,且
;γ为该信道的信噪比,且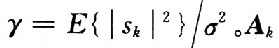 。Ak是一个(2Q+1)×(4Q+1)的矩阵,再利用文献中迭代的方法来计算矩阵的逆。
。Ak是一个(2Q+1)×(4Q+1)的矩阵,再利用文献中迭代的方法来计算矩阵的逆。
2 均衡器算法的FPGA实现
当载波数比较大时,OFDM均衡算法所要计算的矩阵比较庞大,计算量大,很难保证实时性的要求。于是人们很自然地会想到用实时性很强的FPGA来实现均衡器的设计,但是均衡本身所需要处理的数据量和运算量都非常大,即使使用FPGA实现也很困难。
若采用文献中的算法运算量是o(N2),假如当载波数N=128时,运算量还是很大的,无法保证实时性。从均衡效果和运算量两方面考虑,采用了文献中的算法。这是一种典型的迭代算法,效果与文献算法相接近,但是在计算中避免了求一个很大的矩阵的逆运算,而是从频域转移矩阵G中提取出了不大的有效矩阵,这样就减少了大量运算。
2.1 硬件设计思想
在对均衡器算法进行FPGA设计之前,先用Matlab仿真该均衡器浮点算法,通过分析程序可以发现,该算法的核心部分是迭代求逆矩阵的过程。该算法的瓶颈主要是求解由复数元素组成的矩阵的逆的计算量巨大,而且是浮点数会占用很大的存储空间。为尽量减少需要使用的逻辑资源,在进行ISE设计时,数据用16位定点数表示,其中高8位是整数部分,低8位是小数部分。
2.1.1 硬件设计框图
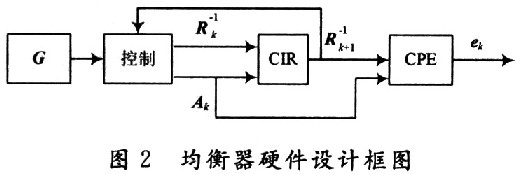
实现该均衡器的硬件设计框图如图2所示,其中G为从Matlab中产生的频域转移矩阵,控制模块完成从G中取出对应的有效值得到Ak,并且控制当一组运算完成后运用上一组产生的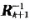 。进行下一组运算,CIR是该算法的核心,即矩阵迭代求逆的运算,CPE模块是一个简单的矩阵运算模块完成
。进行下一组运算,CIR是该算法的核心,即矩阵迭代求逆的运算,CPE模块是一个简单的矩阵运算模块完成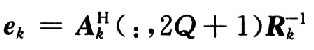 的运算。
的运算。
2.1.2 CIR模块介绍
CIR模块完成矩阵迭代运算过程,它从输入端口读入Ak以及对应的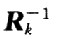 ,采用迭代的方法计算出
,采用迭代的方法计算出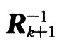 ,用FPGA实现这个模块的端口如图3所示。
,用FPGA实现这个模块的端口如图3所示。
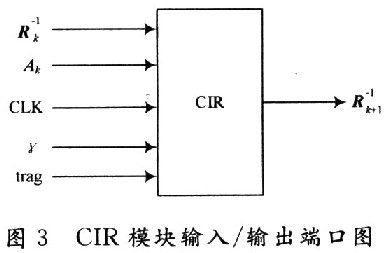
其中,CLK为时钟;γ是模拟信道的信噪比;Ak是频域转移矩阵G中取出的有效矩阵;trag是控制信号,当一次运算结束产生一个有效的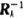 后,只有trag被置为高电平才会进行下一次运算。取Q=2时,
后,只有trag被置为高电平才会进行下一次运算。取Q=2时,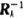 是一个5×5的矩阵。整个求逆矩阵的迭代过程就是从前一个5×5的逆矩阵(即
是一个5×5的矩阵。整个求逆矩阵的迭代过程就是从前一个5×5的逆矩阵(即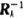 )和从频域转移矩阵G中对应区域取得的5×9的矩阵Ak运算出下一个5×5逆矩阵(即
)和从频域转移矩阵G中对应区域取得的5×9的矩阵Ak运算出下一个5×5逆矩阵(即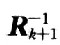 )的过程。
)的过程。
分析其矩阵求逆的迭代算法可以发现,其中大部分完成的是复数矩阵的乘加运算,所有数据是复数,虽然复杂很多,但是实际运算中有许多是多余的。Rk是共轭对称矩阵,上三角部分和下三角部分的实部相同,虚部也只是正负相反,所以只需要算出上三角矩阵的数据,下三角的部分直接对虚部取反就可以了。
Xilinx的FPGA芯片中集成了硬核的乘加器DSP48,可以方便、高速地进行乘加运算。但是本算法中涉及到的复数运算比较灵活,还包括一些减法运算,直接使用DSP48不是很方便的控制。故设计了一种乘加器,使用了乘法器的IP Core,按照要求设置输入输出数据位数,其中的一个乘加运算中设置乘法器的两路输入为8位,输出为16位,调用IP Core如下所示,算法中其他的矩阵运算也都与此类似。

a,b作为两个寄存器储存参与运算的数据,outl是乘法器计算的结果,用fcl进行存放,相累加得到f1,再按照共轭复数运算的规律得到nfl。实现一个8位×8位的乘加器共消耗了56个Slice,32个LUT和49个IOB。该乘加器综合后的RTL结构图如图4所示。
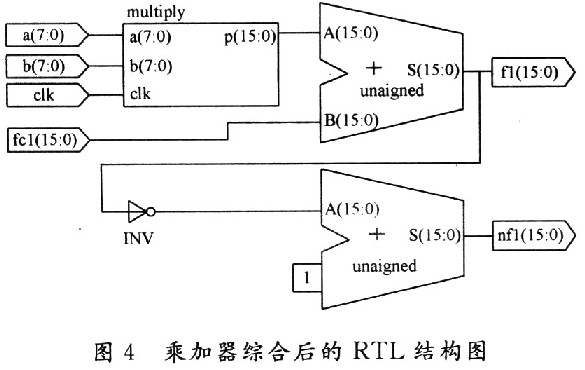
为了能最大限度地提高运算速度,所有数据都用可编程逻辑单元构成的分布式存储器存储并列存储,并且根据算法的要求实现的是多个乘加器同时运算,这样虽然使用了很多逻辑资源,但任何数据都可以即取即用,便于进行大量的并行运算,以提高运算速度。
2.2 系统验证仿真
本系统采用Xilinx公司Virtex-2实验板进行仿真验证,该实验板采用的是XC2VP30芯片,它有30 816个逻辑单元,136个18位乘法器,2 448 KbRAM,资源丰富。开发软件为该公司的集成开发软件平台ISE 9.2,HDL语言采用Verilog,使用Matlab辅助ISE完成FPGA设计的方法。通过实验板上的RS 232串口与PC机进行通信,用Matlab从计算机中传输数据到FPGA芯片中,运算后再通过串口回传均衡后的信号数据到Matlab中仿真验证星座图,以判断该均衡器的效果。
2.2.1 均衡过程
CIR中使用迭代算法避免了并行大向量和大矩阵的运算,而是分步运算。所以对输入信号进行均衡,首先要进行并串变换,但是不需要变成真正的串行信号。当Q=2时,实际上对需要均衡的输入信号Y(i)每次取出5个数据,用yk表示,暂且将这样的变换叫作分组并串变换(P/GS),然后均衡矩阵ek与yk分组完成乘法运算得到一个zk,zk是一个数据不是向量,最后进行串并变换就得到均衡后的信号向量Z(i)。整个均衡的过程如图5所示。
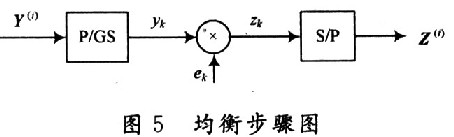
2.2.2 仿真结果
实现该算法的重要一步是所设计的乘加器可以正常使用,并且实时性好。对其进行仿真如图6所示,可以发现当clk发生上升沿跳变时进行计算,图中信号(a,b)表示输入的数据信号;fcl表示相乘的结果;c表示进行乘加以后的运算结果,其计算准确,基本上没有延迟。
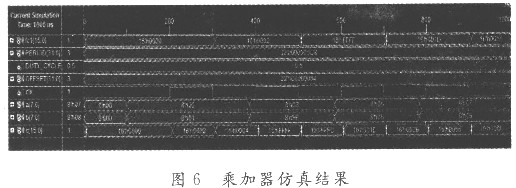
ISE中设计的传输模块实现波特率为19 200 b/s的串口通信控制器,把数据通过RS 232完成FPGA与PC机的双向通信。把均衡后的信号Z(i)传回Matlab中,采用QPSK的星座图进行分析,选择子载波的数目N=128,循环前缀CP的长度为8,并且在认为信噪比被准确估计的情况下均衡的结果,如图7所示。
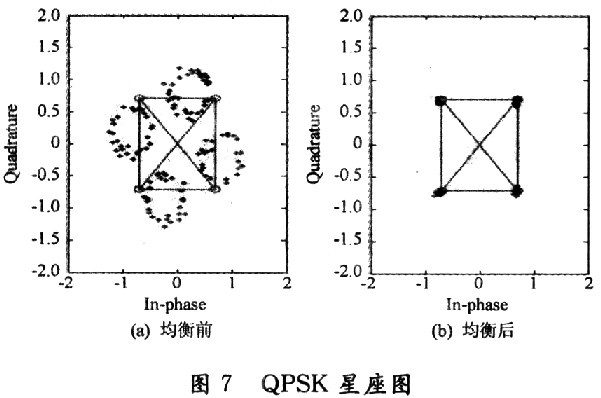
由此星座图可以看出,在均衡前接收到的信号因为多普勒频移和噪声的影响,偏离星座点向周围发散,使用FPGA中均衡以后传回的数据基本没有发散现象。
3 结语
在ISE软件平台上使用Verilog语言实现了一种基于时变OFDM系统的低复杂度MMSE均衡器算法。在Xilinx公司Virtex-2实验板(XC2V930芯片)上对其进行验证,基本达到该算法在Matlab上仿真的均衡效果。但是由于浮点数计算量太大,选用定点数对其进行截取,还是有一定的局限性,在进行大量数据的运算中还是会有些数据不太准确,造成整体的误码率效果不是太好,故还需要进一步改进算法和FPGA的实现方法,以期达到更好的均衡效果。
-
了解图形均衡器与参数均衡器的区别2024-12-26 3832
-
基于FPGA的自适应均衡器的研究与设计2023-11-07 416
-
如何提高自适应均衡器的性能?2021-05-18 2201
-
如何采用FPGA实现可配置均衡器的设计?2021-04-29 1986
-
使用FPGA实现的判决反馈均衡器结构详细资料说明2021-02-05 1155
-
如何使用FPGA实现高速移动下的OFDM均衡器2021-01-27 1010
-
电脑均衡器软件哪个好_电脑均衡器怎么设置才好听2018-05-24 82908
-
信道均衡技术与基于FPGA的自适应均衡器的研究与设计2017-10-26 1184
-
均衡器的工作原理及设计分析2017-09-01 3121
-
高速移动下OFDM均衡器的FPGA实现2012-08-17 2602
-
无线信道仿真和均衡器的FPGA设计与实现2011-10-09 780
-
什么是均衡器2010-02-05 4386
-
均衡器的使用误区2009-12-12 2172
-
基于FPGA的判决反馈均衡器的设计与实现2009-11-30 667
全部0条评论

快来发表一下你的评论吧 !

