

算法面试题:草坪修整
嵌入式技术
1412人已加入
描述
01
故事起源给定一个草坪区间的集合,为使区间互不重叠,最少需要移除多少个区间?
 简单描述如下图,最少移除多少个区间,可以使剩余的区间不重叠。
简单描述如下图,最少移除多少个区间,可以使剩余的区间不重叠。
注:1、区间终点一定大于起点;2、区间[1,2]和[2,3]接触,但不重叠。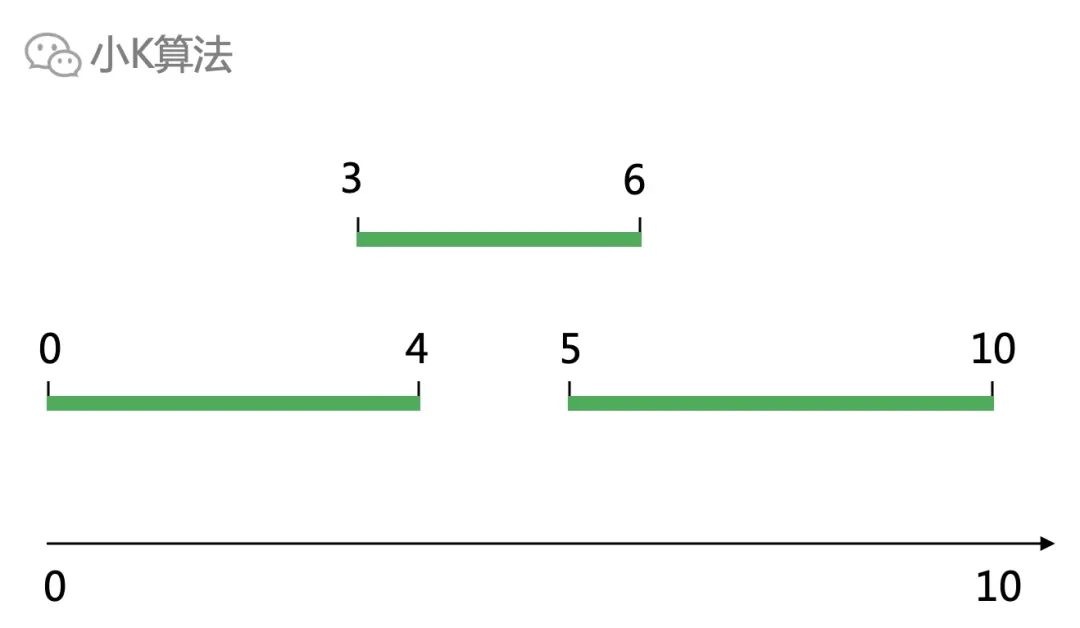 02
分析题目求最少需要移除多少个,其实可以转换问题,变成最多有多少个区间不重叠。
02
分析题目求最少需要移除多少个,其实可以转换问题,变成最多有多少个区间不重叠。
很多时候不容易直接求解时,都可以尝试反向思考,这个技巧非常重要。 所以现在问题就是求最多有多少个区间,使他们落在x轴上不重叠。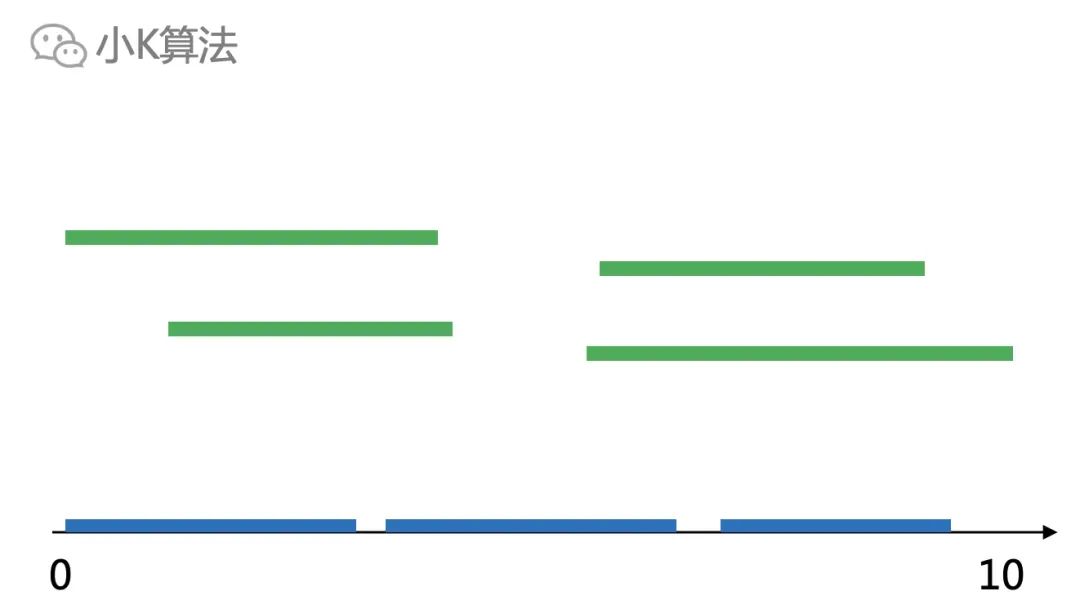 03
最终状态法这里给大家介绍一种非常重要的思考方法,小K称之为“最终状态法”。其本质就是先思考最终要得到的状态,或者说正确结果应该是什么样子。
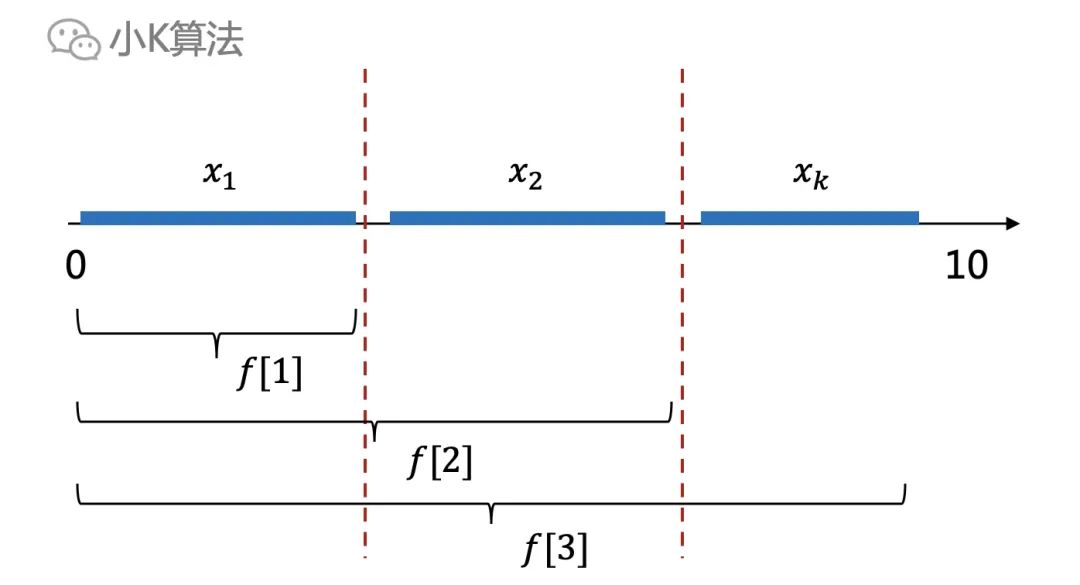
比如这个问题,假设我们已经求出了最优解,那这个最优解,一定是所有的区间中的k个区间,他们能平铺在数轴上且不重叠。下面的蓝色就是我们的答案。
03
最终状态法这里给大家介绍一种非常重要的思考方法,小K称之为“最终状态法”。其本质就是先思考最终要得到的状态,或者说正确结果应该是什么样子。
比如这个问题,假设我们已经求出了最优解,那这个最优解,一定是所有的区间中的k个区间,他们能平铺在数轴上且不重叠。下面的蓝色就是我们的答案。
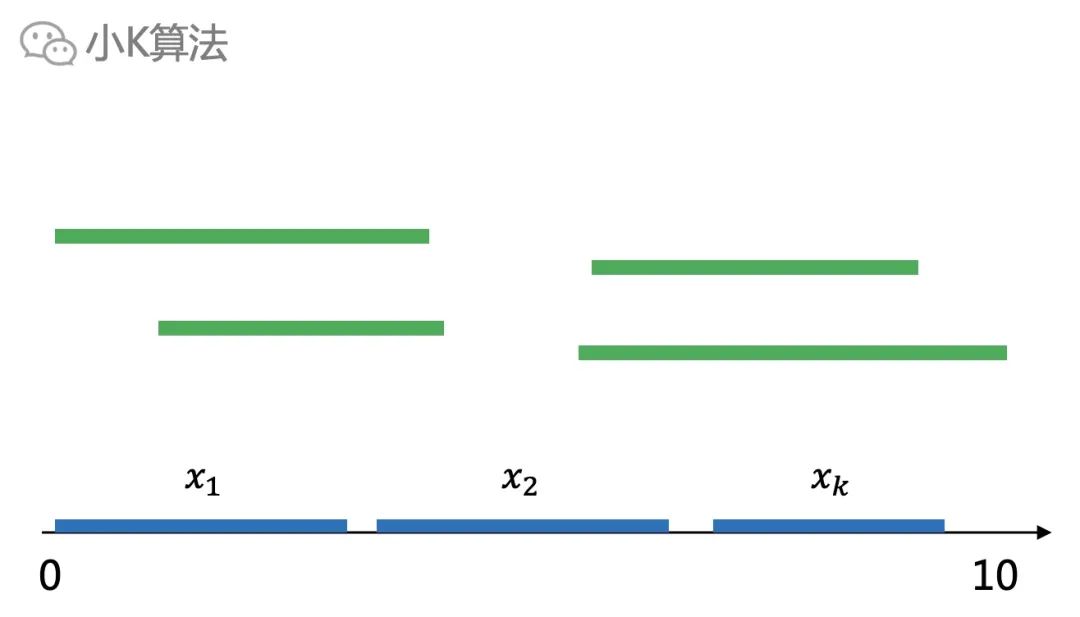 如果我在中间某个位置切一刀,分成两个子问题。现在我问你:左边区间中的解,是否仍然是左边子问题的最优解呢?
如果我在中间某个位置切一刀,分成两个子问题。现在我问你:左边区间中的解,是否仍然是左边子问题的最优解呢?
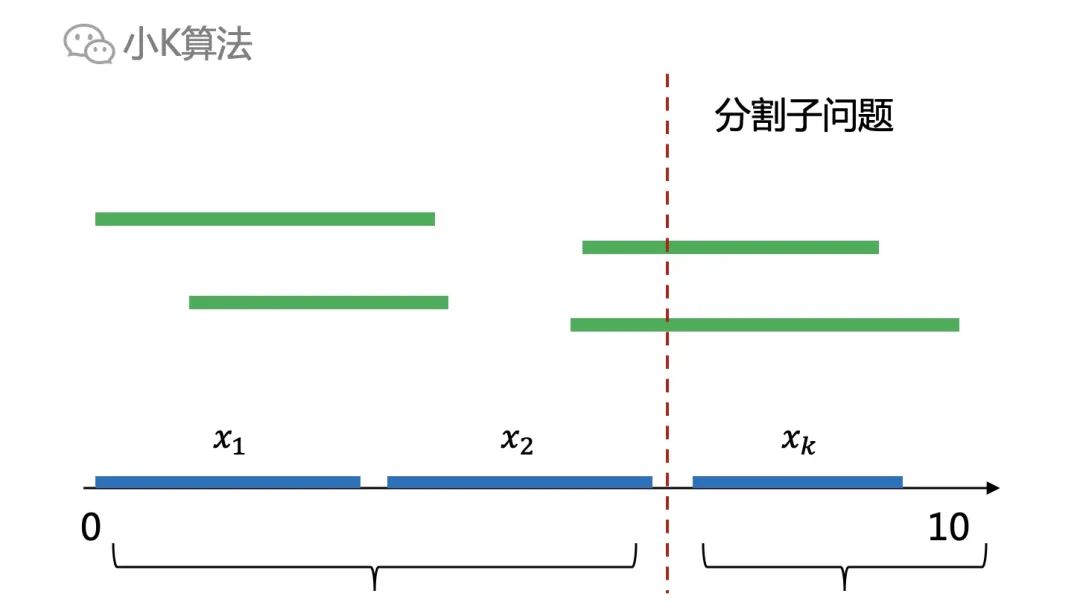 可以用反证法,先假设它不是最优解,那就意味着左边一定还有更优的解,比如下面这样,左边可以选出3个区间。
可以用反证法,先假设它不是最优解,那就意味着左边一定还有更优的解,比如下面这样,左边可以选出3个区间。
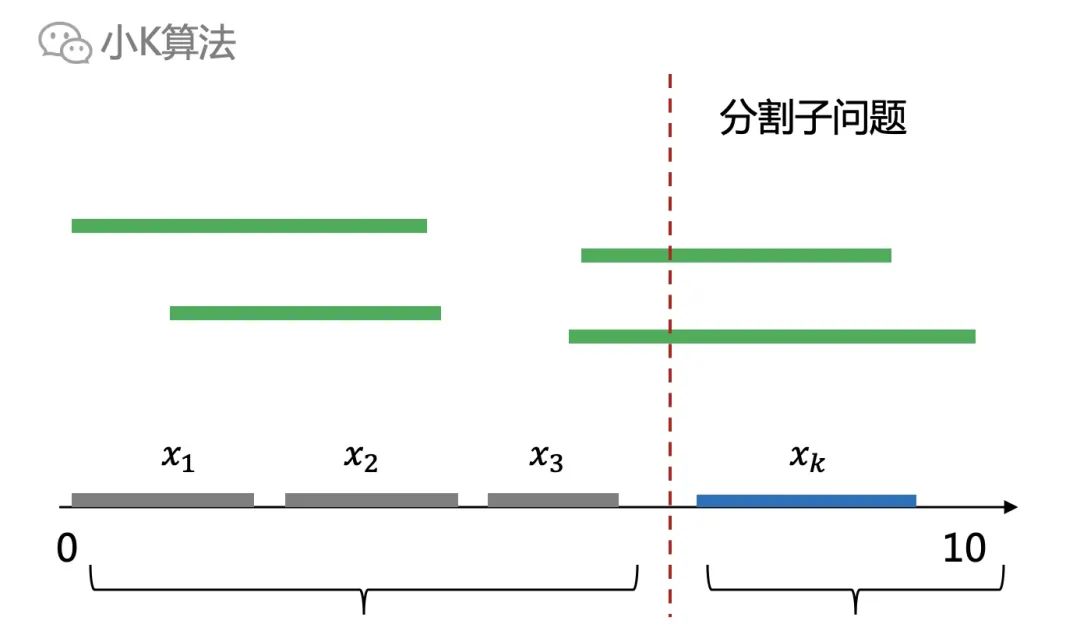 如果再把2个子问题组合起来,那整个问题的最优解应该是4个区间,这和我们之前假设的蓝色是最优解矛盾了。说明分割子问题后,子问题的最优解也一定包含在整个问题的最优解中。
反过来,我们求出了子问题的最优解,就可以递推出大问题的最优解,这就是动态规划的思想。
04
动态规划子问题是沿着数轴进行扩大的,有严格的顺序关系,所以先对区间进行排序。
如果再把2个子问题组合起来,那整个问题的最优解应该是4个区间,这和我们之前假设的蓝色是最优解矛盾了。说明分割子问题后,子问题的最优解也一定包含在整个问题的最优解中。
反过来,我们求出了子问题的最优解,就可以递推出大问题的最优解,这就是动态规划的思想。
04
动态规划子问题是沿着数轴进行扩大的,有严格的顺序关系,所以先对区间进行排序。
设f[i]表示前i个区间中,选择第i个区间作为最后一个区间时的最优解,则f[i]=max(f[j])+1,其中区间j与区间i无重叠。
最大的f[i]就是我们要求的最优解。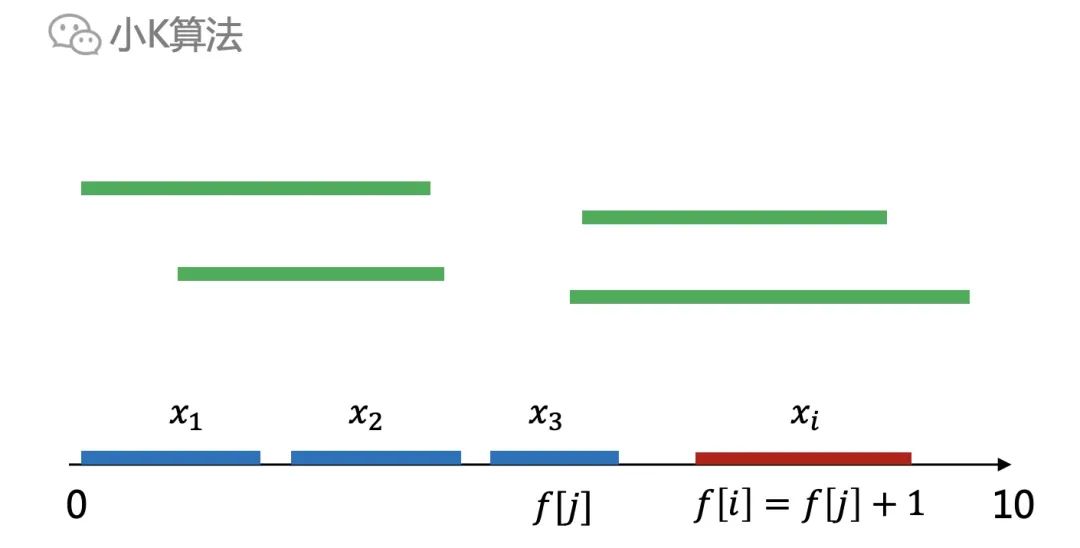 通过递推公式发现,这个模型跟最长上升子序列很像,如果我们把所有的区间绕起点逆时针旋转90度如下,这不就是一个变种的LIS问题了吗。
通过递推公式发现,这个模型跟最长上升子序列很像,如果我们把所有的区间绕起点逆时针旋转90度如下,这不就是一个变种的LIS问题了吗。
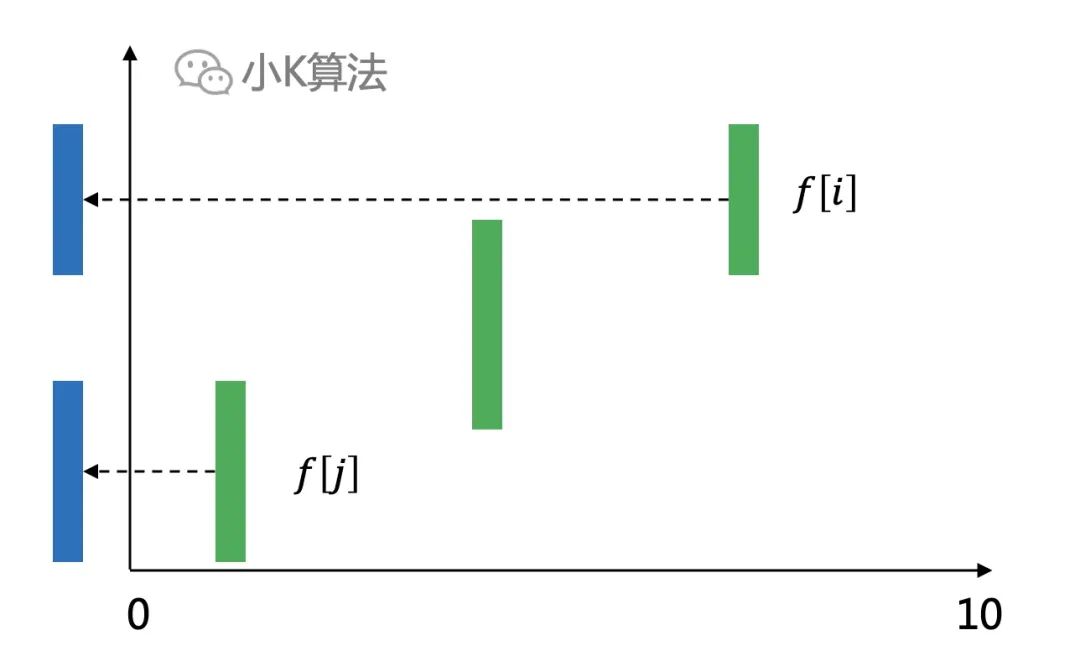 LIS问题可以看成是所有的区间起点都是0,只要求终点要大于之前的终点,而这个问题可以看成区间的起点都不一样,且要求每个区间的起点要大于之前区间的终点。
LIS问题可以看成是所有的区间起点都是0,只要求终点要大于之前的终点,而这个问题可以看成区间的起点都不一样,且要求每个区间的起点要大于之前区间的终点。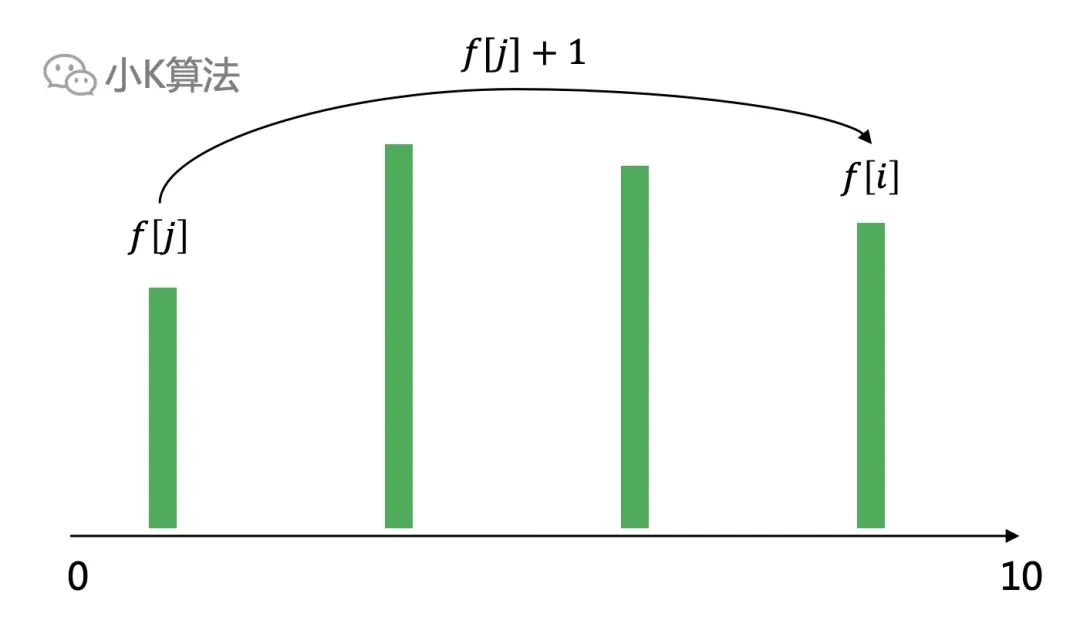 那他们之间的区别又有哪些呢?
1、LIS问题不能排序,因为每个位置都是一个点,所以必须在原来的顺序上,找出最大递增的数量。现在的问题都是区间,只求最终可以放下的数量,与顺序无关,所以可以排序。
2、LIS问题的f[i]可以由前面任意一个f[j]转移过来。现在的问题如果排序完成后,其实不用枚举前面所有的f[j],因为前面一定比后面的小,更大的数轴区间一定可以放下更大的数量啊,所以f[i]其实完全可以从最近的f[j]直接转移。
比如下面,f[3]一定大于等于f[2]。
那他们之间的区别又有哪些呢?
1、LIS问题不能排序,因为每个位置都是一个点,所以必须在原来的顺序上,找出最大递增的数量。现在的问题都是区间,只求最终可以放下的数量,与顺序无关,所以可以排序。
2、LIS问题的f[i]可以由前面任意一个f[j]转移过来。现在的问题如果排序完成后,其实不用枚举前面所有的f[j],因为前面一定比后面的小,更大的数轴区间一定可以放下更大的数量啊,所以f[i]其实完全可以从最近的f[j]直接转移。
比如下面,f[3]一定大于等于f[2]。
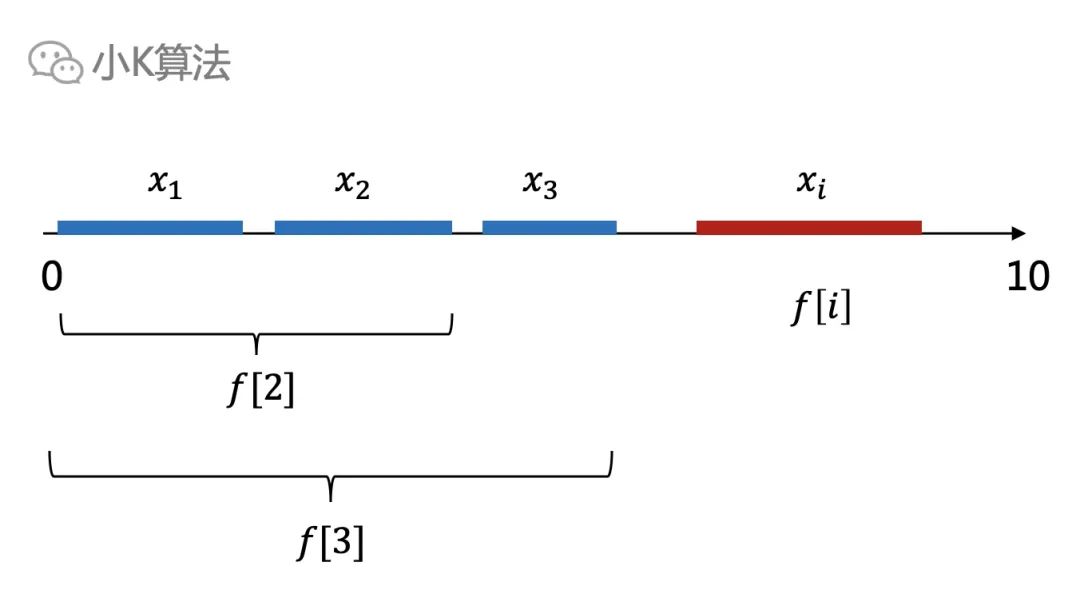 再换一种说法,如果在任何一个位置切一刀,前面是不是都是一个小规模的最优解。再加上前面的结论,每一步只需要从前一个转移过来,这就意味着,每一步都是选择最优的,而且最终得到的结果也是全局最优的。
那这不就是贪心的思想了吗,每一步都选择当前最优的即可。
再换一种说法,如果在任何一个位置切一刀,前面是不是都是一个小规模的最优解。再加上前面的结论,每一步只需要从前一个转移过来,这就意味着,每一步都是选择最优的,而且最终得到的结果也是全局最优的。
那这不就是贪心的思想了吗,每一步都选择当前最优的即可。
 05
贪心动态规划的核心其实是对枚举的优化,它本质也是枚举了所有的情况,只是消除了重复子问题,所以一定能得到最优解。
05
贪心动态规划的核心其实是对枚举的优化,它本质也是枚举了所有的情况,只是消除了重复子问题,所以一定能得到最优解。
而贪心并不是计算了所有的情况,它是在每一步都选择一个最优的,从而保证全局也是最优的。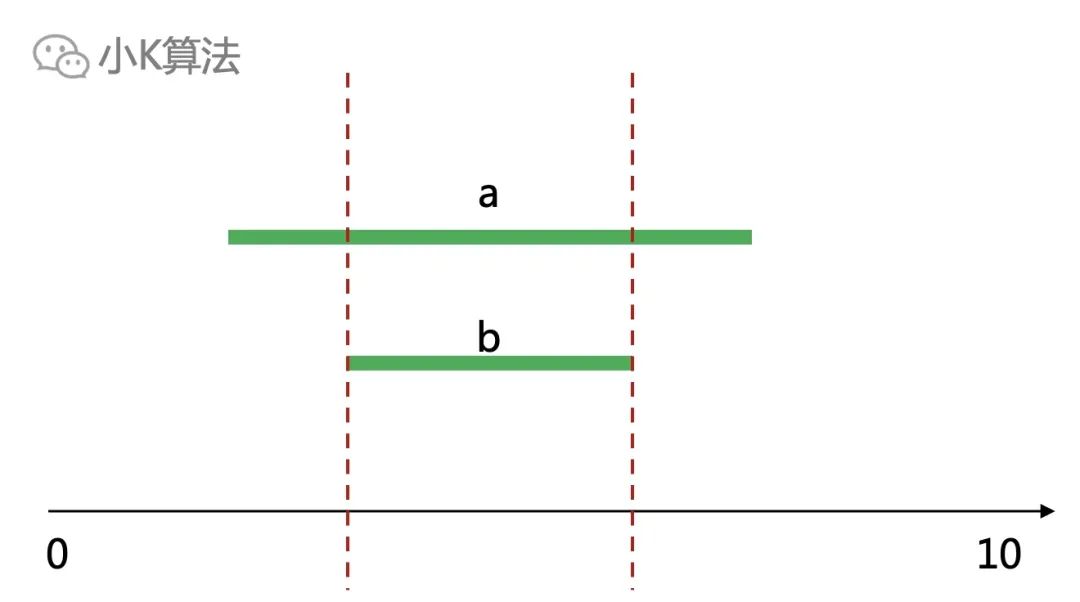 再考虑应该选择哪一个区间作为第一个区间呢?
再考虑应该选择哪一个区间作为第一个区间呢?
如果按区间终点排序,则选择a比选择b更优,因为从左向右求每一步的最优解时,选择a可以给后面的区间留下更多的空间。同理如果按起点排序,就从右向左扫描求解即可。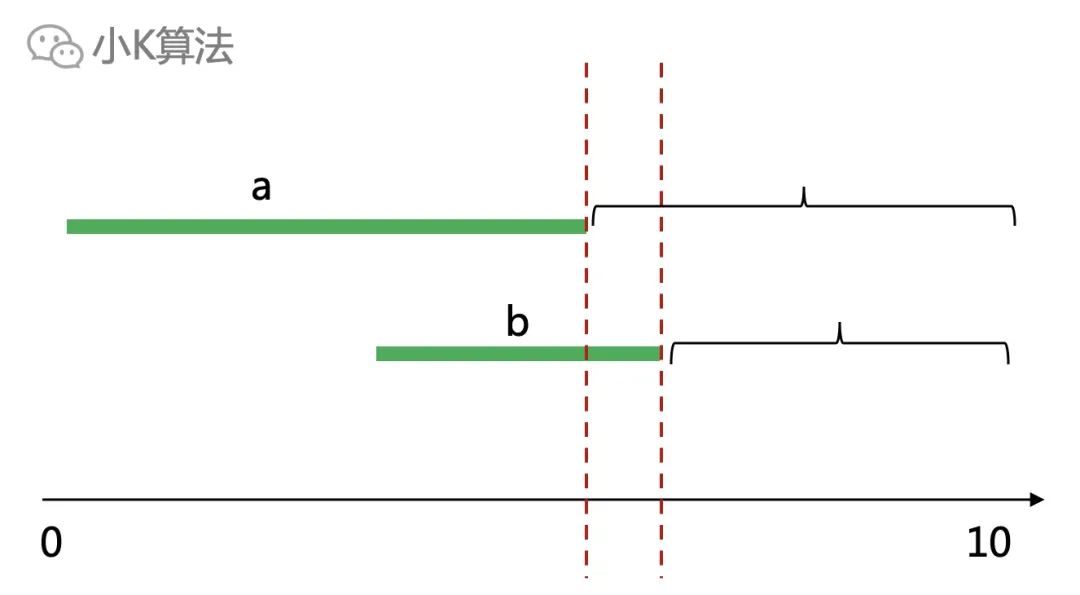
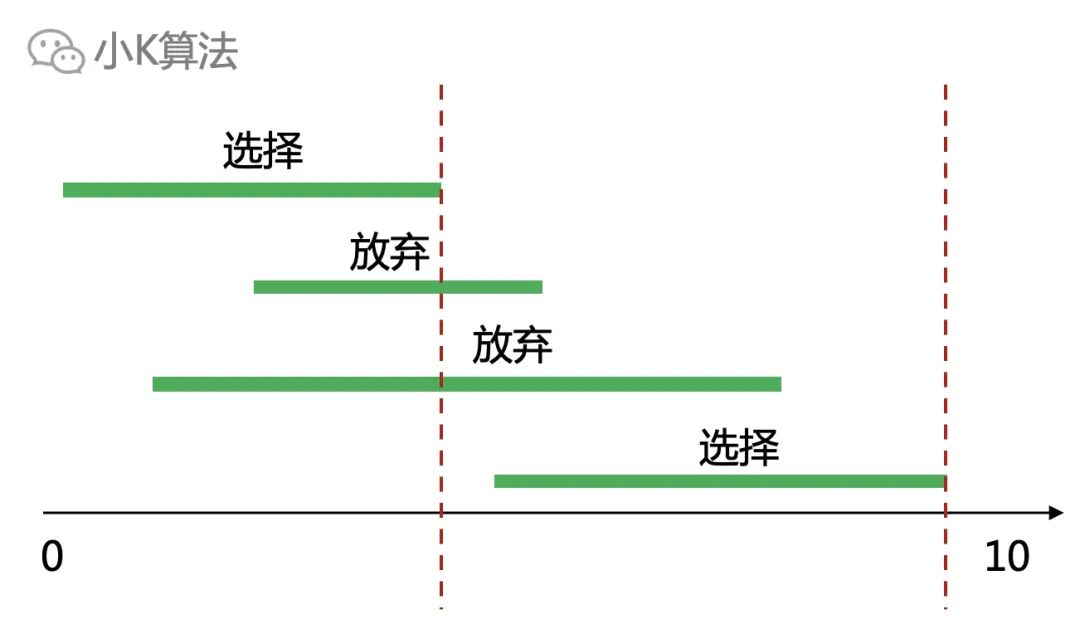
 简单描述如下图,最少移除多少个区间,可以使剩余的区间不重叠。
简单描述如下图,最少移除多少个区间,可以使剩余的区间不重叠。注:1、区间终点一定大于起点;2、区间[1,2]和[2,3]接触,但不重叠。
 02
分析题目求最少需要移除多少个,其实可以转换问题,变成最多有多少个区间不重叠。
02
分析题目求最少需要移除多少个,其实可以转换问题,变成最多有多少个区间不重叠。很多时候不容易直接求解时,都可以尝试反向思考,这个技巧非常重要。 所以现在问题就是求最多有多少个区间,使他们落在x轴上不重叠。
 03
最终状态法这里给大家介绍一种非常重要的思考方法,小K称之为“最终状态法”。其本质就是先思考最终要得到的状态,或者说正确结果应该是什么样子。
比如这个问题,假设我们已经求出了最优解,那这个最优解,一定是所有的区间中的k个区间,他们能平铺在数轴上且不重叠。下面的蓝色就是我们的答案。
03
最终状态法这里给大家介绍一种非常重要的思考方法,小K称之为“最终状态法”。其本质就是先思考最终要得到的状态,或者说正确结果应该是什么样子。
比如这个问题,假设我们已经求出了最优解,那这个最优解,一定是所有的区间中的k个区间,他们能平铺在数轴上且不重叠。下面的蓝色就是我们的答案。
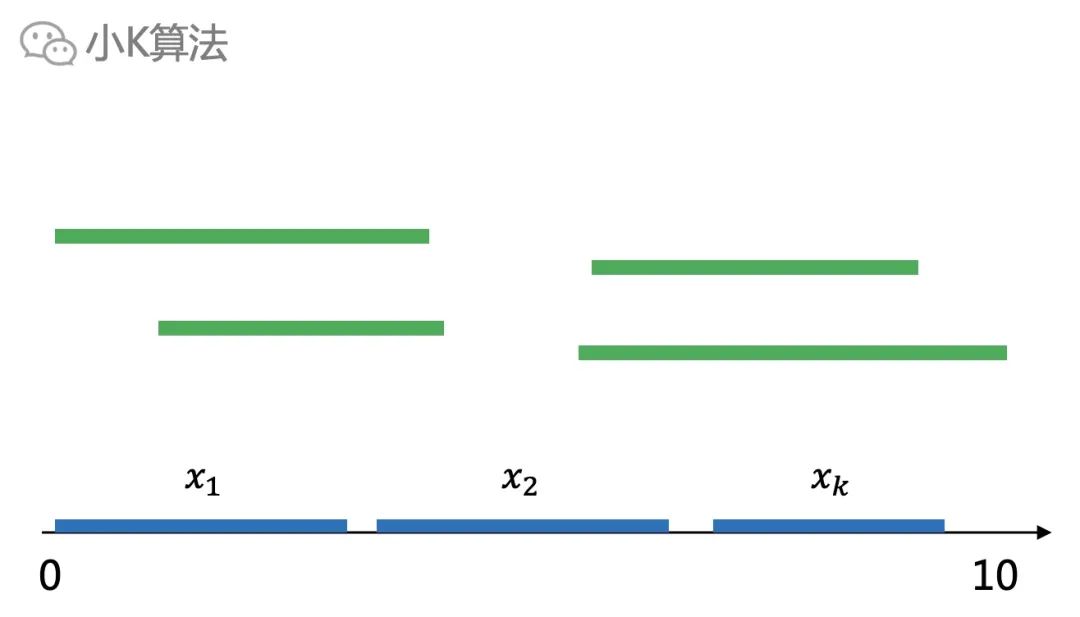 如果我在中间某个位置切一刀,分成两个子问题。现在我问你:左边区间中的解,是否仍然是左边子问题的最优解呢?
如果我在中间某个位置切一刀,分成两个子问题。现在我问你:左边区间中的解,是否仍然是左边子问题的最优解呢?
 可以用反证法,先假设它不是最优解,那就意味着左边一定还有更优的解,比如下面这样,左边可以选出3个区间。
可以用反证法,先假设它不是最优解,那就意味着左边一定还有更优的解,比如下面这样,左边可以选出3个区间。
 如果再把2个子问题组合起来,那整个问题的最优解应该是4个区间,这和我们之前假设的蓝色是最优解矛盾了。说明分割子问题后,子问题的最优解也一定包含在整个问题的最优解中。
反过来,我们求出了子问题的最优解,就可以递推出大问题的最优解,这就是动态规划的思想。
04
动态规划子问题是沿着数轴进行扩大的,有严格的顺序关系,所以先对区间进行排序。
如果再把2个子问题组合起来,那整个问题的最优解应该是4个区间,这和我们之前假设的蓝色是最优解矛盾了。说明分割子问题后,子问题的最优解也一定包含在整个问题的最优解中。
反过来,我们求出了子问题的最优解,就可以递推出大问题的最优解,这就是动态规划的思想。
04
动态规划子问题是沿着数轴进行扩大的,有严格的顺序关系,所以先对区间进行排序。设f[i]表示前i个区间中,选择第i个区间作为最后一个区间时的最优解,则f[i]=max(f[j])+1,其中区间j与区间i无重叠。
最大的f[i]就是我们要求的最优解。
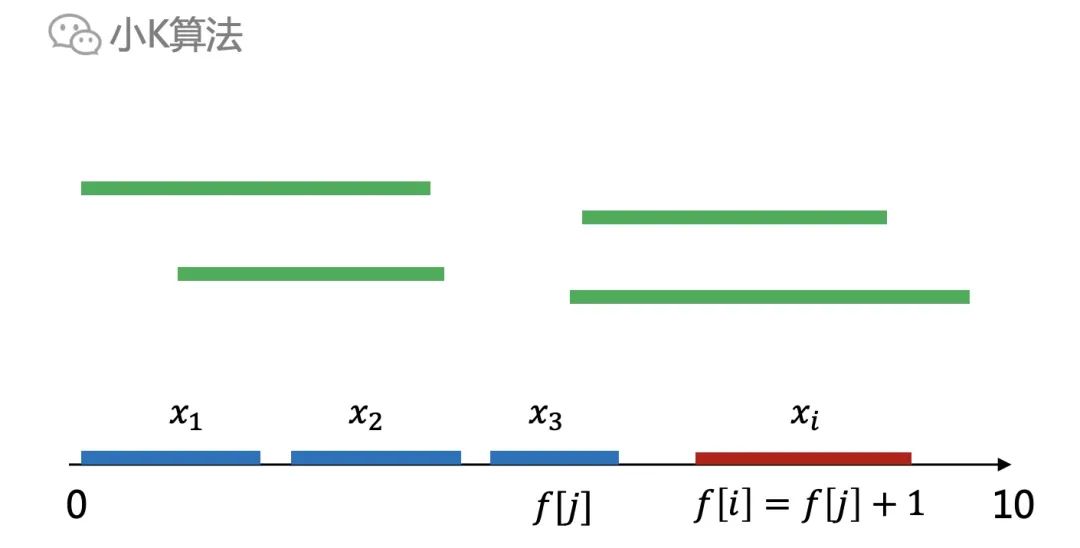 通过递推公式发现,这个模型跟最长上升子序列很像,如果我们把所有的区间绕起点逆时针旋转90度如下,这不就是一个变种的LIS问题了吗。
通过递推公式发现,这个模型跟最长上升子序列很像,如果我们把所有的区间绕起点逆时针旋转90度如下,这不就是一个变种的LIS问题了吗。
 LIS问题可以看成是所有的区间起点都是0,只要求终点要大于之前的终点,而这个问题可以看成区间的起点都不一样,且要求每个区间的起点要大于之前区间的终点。
LIS问题可以看成是所有的区间起点都是0,只要求终点要大于之前的终点,而这个问题可以看成区间的起点都不一样,且要求每个区间的起点要大于之前区间的终点。 那他们之间的区别又有哪些呢?
1、LIS问题不能排序,因为每个位置都是一个点,所以必须在原来的顺序上,找出最大递增的数量。现在的问题都是区间,只求最终可以放下的数量,与顺序无关,所以可以排序。
2、LIS问题的f[i]可以由前面任意一个f[j]转移过来。现在的问题如果排序完成后,其实不用枚举前面所有的f[j],因为前面一定比后面的小,更大的数轴区间一定可以放下更大的数量啊,所以f[i]其实完全可以从最近的f[j]直接转移。
比如下面,f[3]一定大于等于f[2]。
那他们之间的区别又有哪些呢?
1、LIS问题不能排序,因为每个位置都是一个点,所以必须在原来的顺序上,找出最大递增的数量。现在的问题都是区间,只求最终可以放下的数量,与顺序无关,所以可以排序。
2、LIS问题的f[i]可以由前面任意一个f[j]转移过来。现在的问题如果排序完成后,其实不用枚举前面所有的f[j],因为前面一定比后面的小,更大的数轴区间一定可以放下更大的数量啊,所以f[i]其实完全可以从最近的f[j]直接转移。
比如下面,f[3]一定大于等于f[2]。
 再换一种说法,如果在任何一个位置切一刀,前面是不是都是一个小规模的最优解。再加上前面的结论,每一步只需要从前一个转移过来,这就意味着,每一步都是选择最优的,而且最终得到的结果也是全局最优的。
那这不就是贪心的思想了吗,每一步都选择当前最优的即可。
再换一种说法,如果在任何一个位置切一刀,前面是不是都是一个小规模的最优解。再加上前面的结论,每一步只需要从前一个转移过来,这就意味着,每一步都是选择最优的,而且最终得到的结果也是全局最优的。
那这不就是贪心的思想了吗,每一步都选择当前最优的即可。
 05
贪心动态规划的核心其实是对枚举的优化,它本质也是枚举了所有的情况,只是消除了重复子问题,所以一定能得到最优解。
05
贪心动态规划的核心其实是对枚举的优化,它本质也是枚举了所有的情况,只是消除了重复子问题,所以一定能得到最优解。而贪心并不是计算了所有的情况,它是在每一步都选择一个最优的,从而保证全局也是最优的。

 再考虑应该选择哪一个区间作为第一个区间呢?
再考虑应该选择哪一个区间作为第一个区间呢?如果按区间终点排序,则选择a比选择b更优,因为从左向右求每一步的最优解时,选择a可以给后面的区间留下更多的空间。同理如果按起点排序,就从右向左扫描求解即可。



5.3代码实现
vector<vector<int>> a(100, vector<int>(2, 0)); bool cmp(const vector<int> &u, const vector<int> &v) { return u[1] < v[1]; } int main() { int n; cin >> n; for (int i = 0; i < n; ++i) { cin >> a[i][0] >> a[i][1]; } a.resize(n); sort(a.begin(), a.end(), cmp); int ans = 1, right = a[0][1]; for (int i = 1; i < n; ++i) { if (a[i][0] >= right) { right = a[i][1]; ans++; } } cout << n - ans << endl; return 0; } 06 总结这个问题难度不大,但却有很多可以思考的东西在里面,如果直接看问题肯定和LIS没有任何联系,但通过公式发现其本质还是有一些联系在里面。类似的思想很常见,比如如果发现问题符合这种模型,那就又可以用之前写过的一篇LIS问题的优化技巧,单调队列+二分来进行模型的优化。当然算法问题不应太注重固定的套路模型,思考方法才是更重要的,以不变应万变。
审核编辑 :李倩
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
常见的嵌入式C语言面试题2023-07-18 1172
-
关于数组常见的面试题2022-08-17 2239
-
142道linux面试题,值得收藏2022-06-16 617
-
史上最全面Java面试汇总(面试题+答案)精选资料分享2021-07-21 1712
-
操作系统的四十多道题面试题2021-03-10 4113
-
常见的MySQL高频面试题2021-02-08 2963
-
Java的经典面试题和答案详细说明2020-09-07 1243
-
经典硬件面试题精选及解答2017-11-29 1868
-
java经典面试题深度解析2017-06-20 2573
-
C语言经典面试题目2017-01-05 984
-
C语言经典面试题2016-12-20 967
-
c语言面试题集2015-12-18 755
-
java基础练习、面试题2011-07-16 7685
-
c语言面试题,c++面试题下载2008-10-22 747
全部0条评论

快来发表一下你的评论吧 !

