利用FFT算法实现快速傅里叶变换

凡亿PCB 2022-07-10 3193

描述

简介：利用FFT算法实现快速傅里叶变换，在理论、工程中具有非常广泛的应用。除了能够在合适的计算平台完成FFT算法，同时还需要注意到它在频谱分析中可能带来的频率混叠以及频率泄露等问题。

01 Python算法

今天下午的信号与系统，给同学们介绍了离散傅里叶变换的基本应用，并且介绍了快速傅里叶变换(FFT)的主要思想与算法。FFT算法因其优异的性能和广泛的应用，堪称信息处理领域的原子武器。实现FFT编程语言很多，比较来比较去，利用Python语音所描述的该算法最为简明和优雅。

1.1 FFT算法代码

下面的代码是在 The Fast Fourier Transform (FFT): Most Ingenious Algorithm Ever? 视频中给出的 FFT 递归算法形式，最大精度反映了FFT算法核心。

这个代码实现了DIF（时域抽取快速傅里叶变换），利用递归定义，将FFT核心算法中的分而治之体现的淋漓尽致，突出了递归核心中的核心思想。

def FFT(P):
    n = len(P)
    if n * 1: return P

    ye = FFT(P[0::2])
    yo = FFT(P[1::2])

    y = [0]*n
    w = exp(-1j*2*pi/n)
    for j in range(n//2):
        yow = w**j * array(yo)
        y[j] = ye[j] + yow[j]
        y[j+n//2] = ye[j] - yow[j]

    return y

利用Python语音中对于数组切片操作语法，还可以将上面FFT算法中的循环部分都替换成关于数组的操作，使得实际运算速度得到提高。

def FFT1(P):
    n = len(P)
    if n * 1: return P

    ye = FFT(P[0::2])
    yo = FFT(P[1::2])

    w = exp(-1j*2*pi/n)**array(list(range(n//2)))
    yow = w*yo

    y = [0]*n
    y[:n//2] = ye + yow
    y[n//2:] = ye - yow

    return y

1.2 FFT 算法测试

为了测试算法的有效性，下面对于一个方波信号计算对应的FFT结果。

测试算法代码如下：

LEN = 1024
oneLEN=10
p1 = [1]*oneLEN+[0]*(LEN-oneLEN)

y = FFT(p1)
plt.plot(abs(array(y)), label='abs(FFT)')
plt.plot(p1, label='Data')

plt.xlabel("y")
plt.ylabel("abs(FFT(y))")
plt.grid(True)
plt.legend(loc='upper right')
plt.tight_layout()
plt.show()

下面是测试利用Python语言实现的FFT算法计算结果。

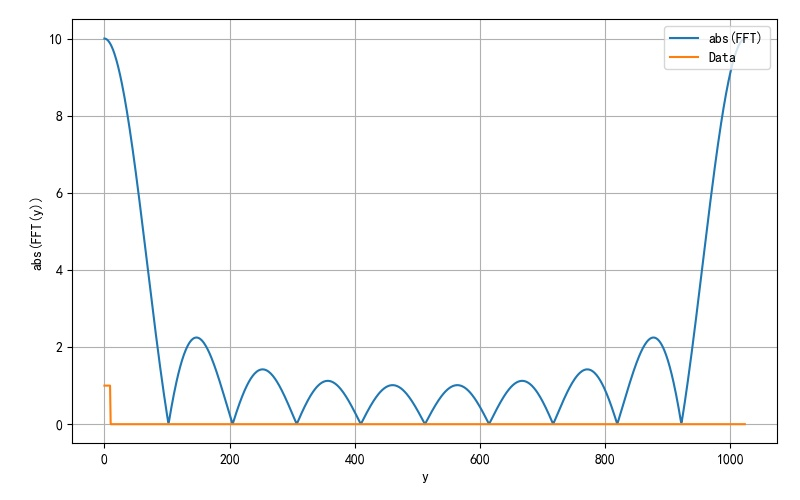▲ 图1.2.1 利用Python语音实现的FFT算法测试结果

02 其它语言FFT

FFT算法贵在计算效率，前面使用Python实现FFT，虽然形式上优雅，但实际执行效率不高。提高执行效率，还是需要使用编译语言。

2.1 Fortran FFT算法

在我上大学期间所学的编程语言为Fortran，估计现在没有多少同学学习这个算法语言。下面给出了利用Fortran语言实现的FFT算法程序。

算法整体上包括有两个阶段：

第一个阶段实现了对输入数据进行倒读顺序排列；
第二阶段利用三重循环实现了分组蝶形运算。

当然了，时过三十年再看Fortran感觉十分酸爽，但它简练语言和执行高效还是让我们回忆起当年编程时所感觉到的快乐。

▲ 图 Fortran 语言实现的FFT算法

2.2 C语言FFT算法

下面是在网络上博文 C++ Program to Compute Discrete Fourier Transform using Fast Fourier Transform Approach^[1] 给出的FFT算法，没有对其功能进行测试。相比于前面利用Python，Fortran来看， C语言实现FFT就显得非常啰嗦了。

#include 
#include 
#include 
#include 
using namespace std;
unsigned int bitReverse(unsigned int x, int log2n) {
    int n = 0;
    int mask = 0x1;
    for (int i = 0; i < log2n; i++) {
        n <<= 1;
        n |= (x & 1);
        x >>= 1;
    }
    return n;
}
const double PI = 3.1415926536;
template<class Iter_T>
void fft(Iter_T a, Iter_T b, int log2n) {
    typedef typename iterator_traits<iter_t>::value_type complex;
    const complex J(0, 1);
    int n = 1 << log2n;
    for (unsigned int i = 0; i < n; ++i) {
        b[bitReverse(i, log2n)] = a[i];
    }
 
    for (int s = 1; s <= log2n; ++s)  {
        int m = 1 << s;
        int m2 = m >> 1;
        complex w(1, 0);
        complex wm = exp(-J * (PI / m2));
        for (int j = 0; j < m2; ++j) {
            for (int k = j; k < n; k += m) {
                complex t = w * b[k + m2];
                complex u = b[k];
                b[k] = u + t;
                b[k + m2] = u - t;
            }
            w *= wm;
        }
    }
}

※ 总 结 ※

利用FFT算法实现快速傅里叶变换，在理论、工程中具有非常广泛的应用。除了能够在合适的计算平台完成FFT算法，同时还需要注意到它在频谱分析中可能带来的频率混叠以及频率泄露等问题。

　　审核编辑：汤梓红

打开APP阅读更多精彩内容