

数控系统刀尖半径补偿方法
描述
车刀刀尖半径补偿是数控车削加工中的常见问题,本文就刀尖半径的影响进行分析,根据不同功能的数控系统进行刀尖半径补偿方法等进行介绍。
编制数控车床加工程序时,理论上是将车刀刀尖看成一个点,如图1a所示的P点就是理论刀尖。但为了提高刀具的使用寿命和降低加工工件的表面粗糙度,通常将刀尖磨成半径不大的圆弧(一般圆弧半径R是0.4—1.6之间),如图1b所示X向和Z向的交点P称为假想刀尖,该点是编程时确定加工轨迹的点,数控系统控制该点的运动轨迹。然而实际切削时起作用的切削刃是圆弧的切点A、B,它们是实际切削加工时形成工件表面的点。很显然假想刀尖点P与实际切削点A、B是不同点,所以如果在数控加工或数控编程时不对刀尖圆角半径进行补偿,仅按照工件轮廓进行编制的程序来加工,势必会产生加工误差。
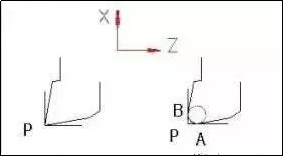
图1 圆头刀假想刀尖一、假想刀尖的轨迹分析与偏置值计算
用圆头车刀进行车削加工时,实际切削点A和B分别决定了X向和 Z向的加工尺寸。如图2所示,车削圆柱面或端面(它们的母线与坐标轴Z或X平行)时,P点的轨迹与工件轮廓线重合;车削锥面或圆弧面(它们的母线与坐标轴Z或X不平行)时,P点的轨迹与工件轮廓线不重合,因此下面就车削锥面和圆弧面进行讨论:
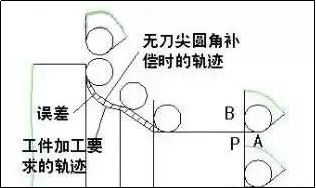
图2 刀尖圆弧半径的影响1、加工圆锥面的误差分析与偏置值计算
如图3a所示,假想刀尖P点沿工件轮廓CD移动,如果按照轮廓线CD编程,用圆角车刀进行实际切削,必然产生CDD1C1的残留误差。因此,实际加工时,圆头车刀的实际切削点要移至轮廓线CD,沿CD移动,如图3b所示,这样才能消除残留高度。这时假想刀尖的轨迹C2D2与轮廓线CD在X向相差ΔX,Z向相差ΔZ。设刀具的半径为r,可以求出:
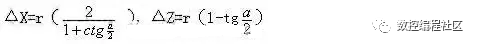
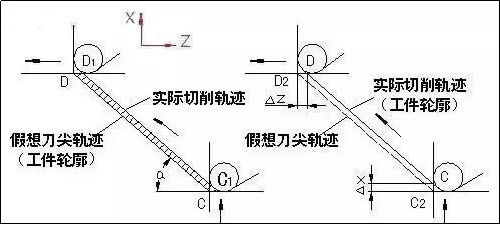
图3 圆头车刀加工圆锥面
2、加工圆弧面的误差分析与偏置值计算
圆头车刀加工圆弧面和加工圆锥面基本相似。如图4是加工1/4凸凹圆弧,CD为工件轮廓线,O点为圆心,半径为R,刀具与圆弧轮廓起点、终点的切削点分别为C和D,对应假想刀尖为C1和D1。
对图4a所示凸圆弧加工情况,圆弧C1D1为假想刀尖轨迹,O1点为圆心,半径为(R+r);对图4b所示凹圆弧加工情况,圆弧C2D2为假想刀尖轨迹,其圆心是O2点,半径为(R-r)。如果按假想刀尖轨迹编程,则要以图中所示的圆弧C1D1或C2D2(虚线)有关参数进行程序编制。
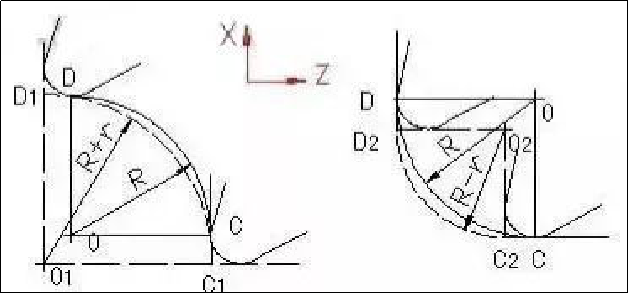
图4 圆头车刀加工90°凸凹圆弧
二、刀尖圆角半径补偿方法
现代数控系统一般都有刀具圆角半径补偿器,具有刀尖圆弧半径补偿功能(即G41左补偿和G42右补偿功能),对于这类数控车床,编程员可直接根据零件轮廓形状进行编程,编程时可假设刀具圆角半径为零,在数控加工前必须在数控机床上的相应刀具补偿号输入刀具圆弧半径值,加工过程中,数控系统根据加工程序和刀具圆弧半径自动计算假想刀尖轨迹,进行刀具圆角半径补偿,完成零件的加工。刀具半径变化时,不需修改加工程序,只需修改相应刀号补偿号刀具圆弧半径值即可。需要注意的是:有些具有G41、G42功能的数控系统,除了输入刀头圆角半径外,还应输入假想刀尖相对于圆头刀中心的位置,这是由于内、外圆车刀或左、右偏刀的刀尖位置不同。
当数控车床的数控系统具有刀具长度补偿器时,直接根据零件轮廓形状进行编程,加工前在机床的刀具长度补偿器输入上述的ΔX和ΔZ的值,在加工时调用相应刀具的补偿号即可。
对于有些不具备补偿功能经济型数控系统的车床可直接按照假想刀尖的轨迹进行编程,即在编程时给出假想刀尖的轨迹,如图3b和图4所示的虚线轨迹进行编程。如果采用手工编程计算相当复杂,通常可利用计算机绘图软件(如AutoCAD、CAXA电子图版等)先画出工件轮廓,再根据刀尖圆角半径大小绘制相应假想刀尖轨迹,通过软件查出有关点的坐标来进行编程;对于较复杂的工件也可以利用计算机辅助编程(CAM),如用CAXA数控车软件进行编程时,刀尖半径补偿有两种方式:编程时考虑半径补偿和由机床进行半径补偿,对于有些不具备补偿功能数控系统应该采用编程时考虑半径补偿,根据给出的刀尖半径和零件轮廓会自动计算出假想刀尖轨迹,通过软件后置处理生成假想刀尖轨迹的加工程序。对于这类数控系统当刀具磨损、重磨、或更换新刀具而使刀尖半径变化时,需要重新计算假想刀尖轨迹,并修改加工程序,既复杂烦琐,又不易保证加工精度。
以上通过车刀刀尖半径对加工工件的影响的分析可知,要保证零件加工精度,在数控加工尤其精加工一定要进行车刀刀尖半径补偿。由于目前数控系统的功能参差不齐,针对不同类型数控系统,在实际应用中采取方法也不同,有些在编程时就要考虑半径补偿,有些可在机床中进行半径补偿。
审核编辑:汤梓红
-
数控系统参数丢失的处理方法2023-10-21 2880
-
数控系统常见的故障诊断与维修方法有哪些2019-11-04 10631
-
数控系统有哪些2019-08-24 42698
-
数控系统维修2016-05-23 929
-
数控系统加减速的实现方法2016-05-03 681
-
CNC数控系统加减速控制方法研究与实现2016-04-26 727
-
车床经济型数控系统硬件设计2011-06-21 903
-
刀具半径补偿分析2011-06-07 7267
-
基于综合智能计算的数控系统误差补偿2011-05-19 1501
-
基于PC的开放式数控系统的研究与开发2009-08-24 645
-
五轴联动数控系统的开放化设计2009-06-13 1617
-
数控系统的组成原理2009-02-16 1643
-
数控系统的原理及组成2008-12-30 7497
全部0条评论

快来发表一下你的评论吧 !

