从卡诺定理如何到熵增加原理？

从卡诺定理如何到熵增加原理？这篇文章为你来捋一捋思路。

1824年，法国科学家卡诺提出：工作在两个恒温热源之间的一切热机，以可逆热机的效率为最高。此即卡诺定理。

在历史上，卡诺定理曾是热力学第二定律的基础，但现在，它可从热力学第二定律推得，具体方法是采用反证法，下面先来讲一讲这个证明过程。

01

证明卡诺定理

现考虑两个热机M和M'，其中M为可逆热机，而M'为一般热机，即M'有可能是可逆热机，也有可能是不可逆热机。

两台热机都工作在两个热源  和  之间，设  。假设它们从高温热源  吸热分别为  和  ，且  。向低温热源  放热分别为  和  ，做功分别为  和  ，效率分别为  和  。

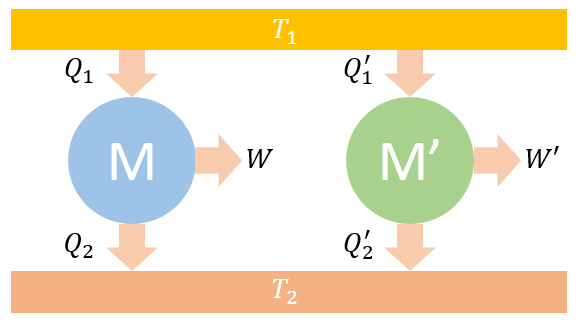
用反证法，设  ，则 由于  ，故  ，既然M是可逆的，则可将  的一部分拿来推动M逆向工作，即让M成为一个制冷机。所以M现在从低温热源  吸热  ，向高温热源放热  。

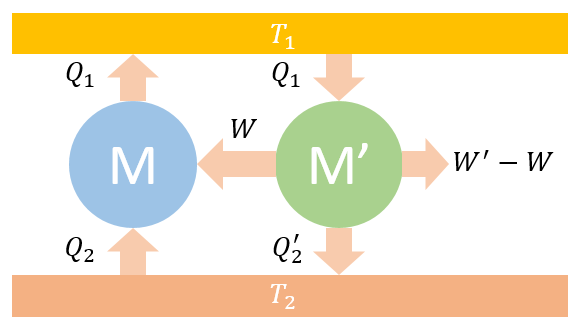
把这两个热机联合成一个总热机M''，该总热机与  没有热交换，只与  发生热交换，其值为  ，同时总热机对外做功为  。

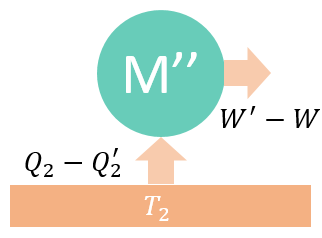
显然，这等于实现了“从单一热源吸热并做功而不产生其他影响”的美梦，违反了热力学第二定律的开尔文表述。这说明前面的假设是错误的，正确的结果只能是 如果M为一般热机，而M'为可逆热机，那么也会得到 所以，当M和M'都为可逆热机时，上面两式同时成立，那只能是 所以，工作在两个恒温热源之间的一切可逆热机的效率相等，工作在两个恒温热源之间的任何热机的效率不可能比可逆热机的高。

这就证明了卡诺定理了。它看起来就像一条数学定理，的确，要不然怎么叫定理呢？物理中的定理是一种可以证明的命题。这一点与物理定律不同，物理定律是从实验中归纳总结出来的，无法也无须证明。

02

澄清一个误解

值得注意的是，卡诺定理强调了一点：工作在两个恒温热源之间的热机！

这意味着什么呢？

这意味着，你的热机只能与两个恒温热源发生热交换，除此之外的过程，系统不能再吸放热，这正好就是卡诺循环的要求嘛！

所谓卡诺循环是指，工作物质只与两个恒温热源交换热量，除此之外，不再存在任何吸放热的过程。

所以，工作在两个恒温热源之间的循环就是卡诺循环！工作在两个恒温热源之间的热机就是卡诺热机。

因此，卡诺定理中提到的热机必然是卡诺热机，只是分为可逆或不可逆罢了。

温馨提示：很多人认为卡诺循环一定是可逆的，这是一种误解，卡诺循环只是规定工作物质工作在两个恒温热源之间，并没有说过程一定可逆！

如果卡洛循环还是可逆的，且工作物质是理想气体，由于热机交换热的时候经历的是等温变化，所以必然对应两条等温线。而理想气体的等温线不会相交，要构成循环，必须还要另外两条线来帮忙！而另一方面，既然已经要求该热机不能与别的热源交换热，这另外的两条线必然都是绝热线。所形成的循环就是理想气体的准静态的卡诺循环，也就是可逆的卡诺循环，其P-V图如下所示。

 

 

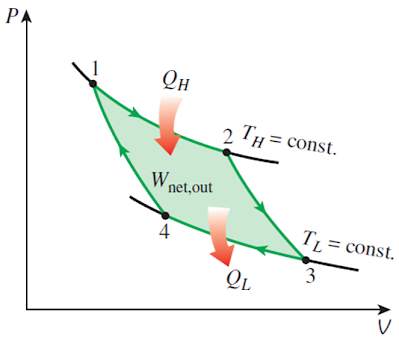
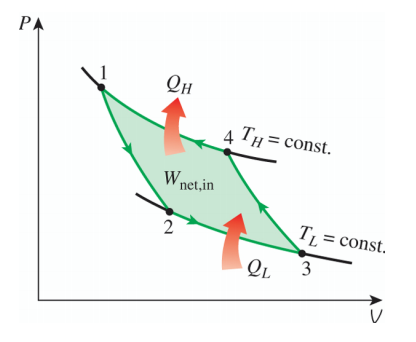
如果卡诺循环不是可逆的，那循环过程不是准静态的，也就没法用曲线来表示了，只能通过一个热机模型图来表示，如下图所示。

 

 

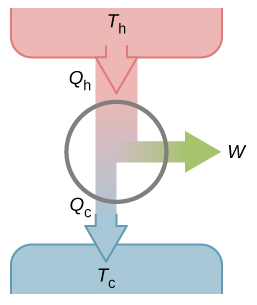
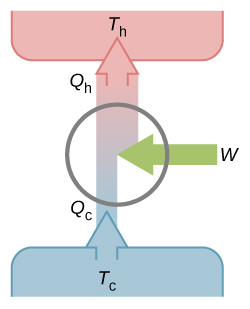
至于有人说：可逆的卡诺热机的效率最高。

这是不对的！

因为，对于工作在非卡诺循环上的热机来说，其效率不一定比可逆卡诺热机小。其实，非卡诺热机的效率要另当别论，因为它们与卡诺定理没有关系。

当然，一切热机的效率肯定不会达到1，这是热力学第二定律决定的。

03

理想气体的卡诺循环

要注意，前面提到的卡诺循环是普遍的，并没有限制工作物质的种类，所以卡诺定理对任意工作物质都成立。换句话说，无论热机的工作物质是什么，只要是工作在两个确定温度的热源之间的可逆热机，其效率都一样！

因此，当根据一种特殊而熟悉的工作物质——理想气体来具体分析时，得到的可逆卡诺循环的效率应该就代表了任何可逆卡诺热机效率！

考虑一定质量的理想气体，设它经历一个顺时针的准静态卡诺循环，也就是沿着由两条等温线和两条绝热线围成的回路。

这个过程比较繁琐，但大多数热学书上都有，这里就直接给出结果吧。

经过计算得，理想气体的可逆卡诺循环的效率为 其中  是高温热源的温度，  是低温热源的温度。 这就是工作在高温 和低温  之间的一切可逆卡诺热机的效率。

既然得到了可逆卡诺热机效率的值，那么卡诺定理现在可表述为 左边代表一般卡诺热机的效率，右边代表可逆的卡诺热机的效率。 

04

克劳修斯不等式

根据卡诺定理可知 即 由于  实际上是代表放热，如果约定放热用负数表示，那么上式应该改为 因此得到 我们将每一项叫做热温比。由此可见，卡诺循环的热温比之和小于或等于零，等号在循环可逆时成立。此式是任何卡诺循环都满足的要求。

由于这两个温度一高一低，分别吸热和放热，如果用  表示高温， 用 表示低温，用  表示放热，用  表示吸热，则上式可以写成 对任意一个循环过程，如下图中的循环ABCDA，我们总可以将其分割成无数个卡诺循环，那么，整个循环相当于这些卡诺循环的总和。

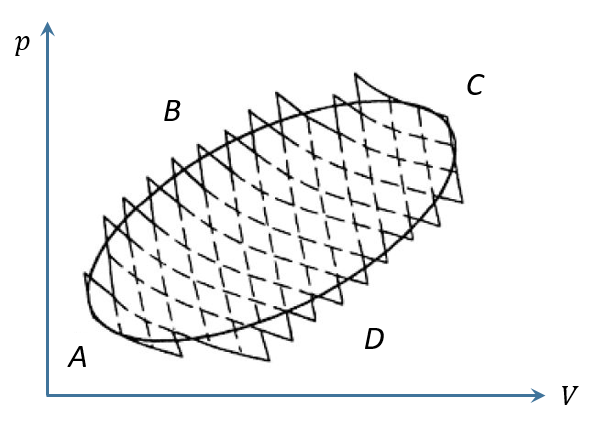
每个卡诺循环对应两个温度，相邻的卡诺循环会共用一个温度，从左至右，这些温度依次是  ，  ，  ，  ，  。

注意，这里的  一般应为无穷大，否则不能确保一个任意的循环能被分割成卡诺循环。

由于每个卡诺循环  有一个高温  和一个低温  ，都满足上面的不等式，若将所有卡诺循环的不等式加起来，就是 

由于每相邻的两个卡诺循环都共用一条等温线，这条等温线在两个卡诺循环中的贡献会合成一项。例如，对第  条等温线来说，它在前一个循环  上吸热  ，在后一个循环  上放热  ，二者抵消后得到的总热值就是这条等温线上的热交换量，记作 

由于第1条和第  条等温线都没有被两个卡诺循环共有，所以 因此，这第  条等温线对应的项为  ，也就是一个热温比。既然每条等温线都对应一个热温比，把所有这些热温比都加起就是

若上述分割的每个卡诺循环无限小，则上式就变成连续的求和，也就是积分，即 

这就是大名鼎鼎的克劳修斯不等式。

05

热力学熵的定义

对克劳修斯不等式来说，当循环过程可逆时，等号成立；当循环过程不可逆时，小于号成立。

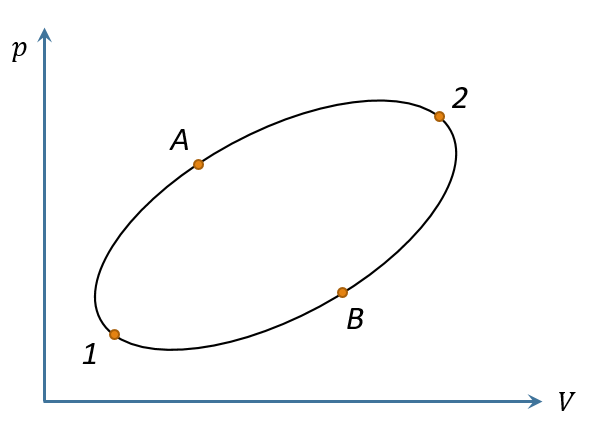
对上图所示循环过程1→A→2→B→1，则有

将其分成过程1→A→2和2→B→1，则 即 这说明热温比  的积分与路径无关，或者说，它的积分只取决于始末两点，因此必定存在一个由状态决定的函数  ，它在始末两点的取值之差刚好等于  的沿任意可逆路径的积分，即 可逆

关于“为什么必定存在一个由状态决定的函数”这一点，可与保守力做功类比，势能函数也是类似得到的。具体可参看文章《什么是保守力？》的第4节的有关推导。

这个状态函数  就是克劳修斯熵，也叫热力学熵。上式即为热力学熵的定义式。对一个微小的过程来说，熵的微分就是热温比，即 

注意，热力学熵的定义并没有给出熵的绝对值，只给出了熵在不同状态的改变量，这个改变量是通过计算热温比在连接两个态的可逆路径上的积分来获得。

虽然熵的值本来只与状态有关，但现在没法知道它到底如何由状态决定，所以只能通过计算热温比的积分来获得它在不同态之间的差值。

根据热力学第一定律， 再结合熵的微分关系可知 此式将热力学第一、第二定律结合起来了，避免了非状态量，是最一般的热力学关系，称之为热力学基本方程。根据此方程，可以通过构造合适的可逆过程来计算不同态之间的熵差。 

06

熵增加原理

再次回到克劳修斯不等式 上面通过分析等号的情形引入了熵的定义，那么如果考虑一个一般的循环会有什么结果呢？ 

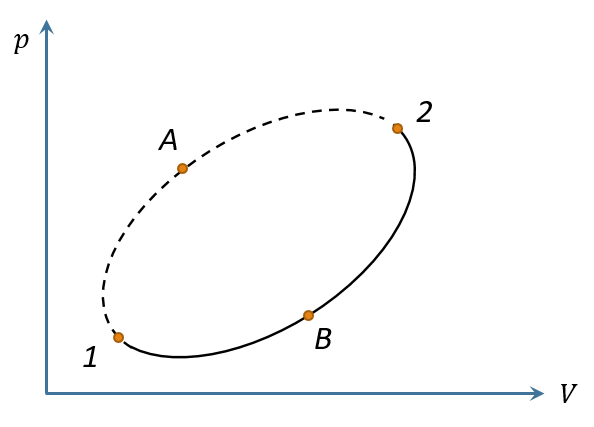
考虑一个循环1→A→2→B→1，设2→B→1是可逆过程，但1→A→2是一般过程，即可能可逆也可能不可逆。根据克劳修斯不等式有则 也就是 而既然2→B→1是可逆过程，根据熵的定义，有 故得 令  ，考虑到1→A→2是一般过程，直接记为1→2即可，因此上式可写为 此式告诉我们，任意过程中的热温比的积累不会比它连接的两个态的熵差大。

对绝热过程，显然右边为零，因此 这说明，绝热过程的不会减少。而孤立系统经历的过程当然是绝热的，因此孤立系统的熵永不减少，这就是熵增加原理。

根据熵增加原理，对孤立系统而言，除非经历可逆过程，否则熵就会增大！由于实际中可逆过程很难实现，所以熵增加原理告诉我们：实际中的孤立的系统熵一般都是增加的。

07

循环和非循环过程的熵变

热力学过程可能是循环，可能是有始有终的过程，下面分别看看它们对应的熵变。

先来看循环过程。

既然循环是指回到了初态，初末态相同，而熵是态函数，只跟位置有关，因此循环过程无论可逆与否，均有  。所以，循环过程不存在考虑熵变的问题！

不过需要注意的是，循环没有熵变不是指任何两点之间没有熵变，而是指一个完整的的循环不会导致熵变，且没有考虑外界的情况。

另外，根据克劳修斯不等式 若为可逆循环，上式取等号，而若为不可逆循环，则取小于号。

再来看非循环的过程。 

根据上节的结论，对任意过程，熵增不会比热温比的积累小，即

当过程可逆时且不绝热时，则有   

注意，此时热温比的积累可正可负，取决于是放热还是吸热，若是放热，熵减少，反之则熵增加。

当过程可逆又绝热时，则有 

当过程不可逆且不绝热时，则有 

注意，此时热温比的积累可正可负，取决于是放热还是吸热，若是放热，熵可能减少也可能增加，若是吸热，则熵必然增加。

当过程不可逆且绝热时，则有 这就是最常见的孤立系统的情形，熵增加原理也是因之而得其名。

审核编辑 ：李倩