Python实现所有算法-基本牛顿法

Python实现所有算法-二分法

Python实现所有算法-力系统是否静态平衡

Python实现所有算法-力系统是否静态平衡（补篇）

Python实现所有算法-高斯消除法

Python实现所有算法-牛顿-拉夫逊（拉弗森）方法

Python实现所有算法-雅可比方法（Jacobian）

Python实现所有算法-矩阵的LU分解

Python实现所有算法-牛顿前向插值

兄弟们！今天的简单，我直接给大家表演徒手求导。

求导是数学计算中的一个计算方法，它的定义就是，当自变量的增量趋于零时，因变量的增量与自变量的增量之商的极限。在一个函数存在导数时，称这个函数可导或者可微分。可导的函数一定连续。不连续的函数一定不可导。

这个图一定不可以错过

基本的做法是这样的

对于一种数学的运算，我们总是给出满足的规则

其实哇，这些东西我写的没有意义，在座的各位都学过高等数学，数学分析，而且高中还学了两年。概念不是啥问题。

如果是为了科普，我推荐这本可爱的漫画书（是数学书啦~）

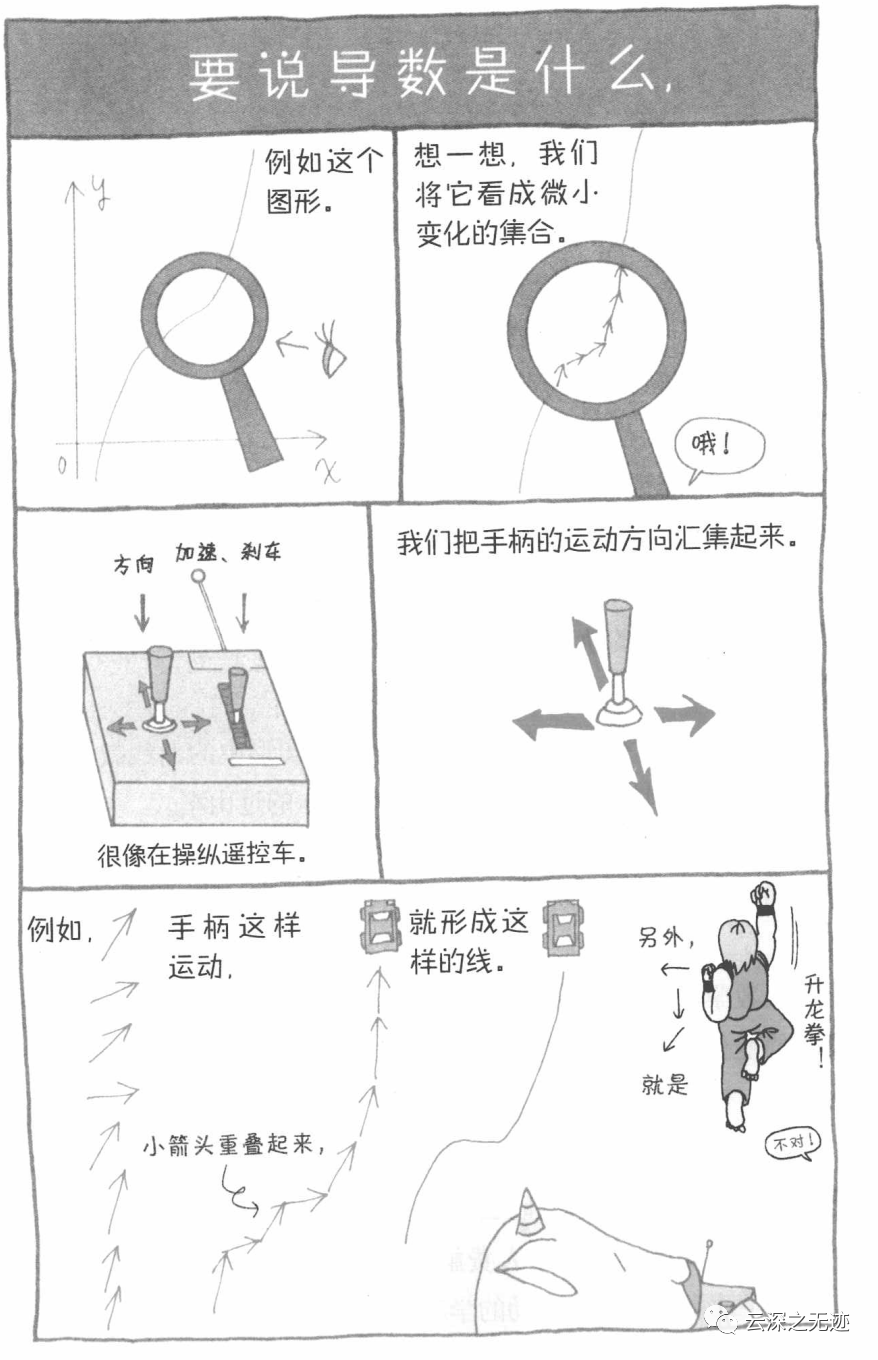
给大家看一个简单的页面，是不是很有趣

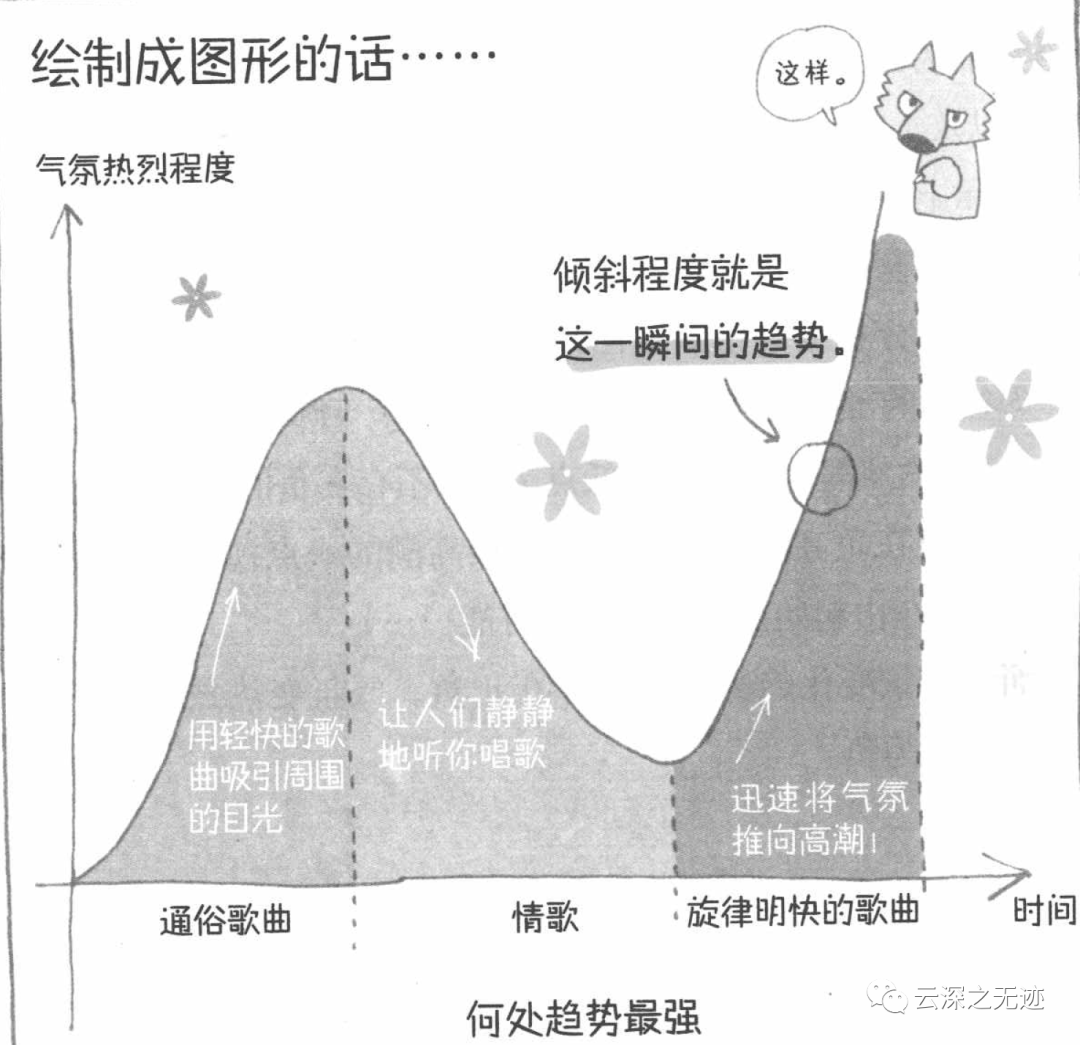
对一首歌的趋势的曲线说明

书中的内容可能不深，但是这种寓教于乐的方式真的很好，至少这就是大众接受的数学。

 

其次我推荐这本书，你有没有想过微积分风风雨雨这么多年，诞生之初是什么样的？

本书给你答案

 

这本书我可太喜欢了，点到为止，是我对本书的评价，是一本真的可以一本书读下去的数学书。

随便截图一个，点明对我们的需求来说，这样就足够了

非常的简洁，很OK

还有一套是托马斯微积分，awesome的好书，1k5多的页数，让人直呼过瘾

另外张景中院士的直来直去微积分真的很有特色，本书的特点是不使用极限和无穷小的概念，直截了当的给出函数的基本概念。

这段话是对书的最好诠释

真的这些书给人以舍不得读下去的感觉，因为读完就没有了

如果上面的你觉得太简单了，微积分笔记这本书是对于数学分析方方面面的一个题集总结。

有代表性的习题加上简短的定理总结，不可多得好书

因为Latex的排版，在美观上面也是香的一比

emmmm，如果你想在通俗和严谨之间得到一个平衡，我个人觉得经济学的教材是很好的。

最后让我再推荐一下黄皮书，yyds！！！

同系列的还有这本，还有一本是线性代数就该这样学

在最后让我隆重的安利一下，全美经典的教材，统计学原理讲的真的是NO.1

内容丰富嗷

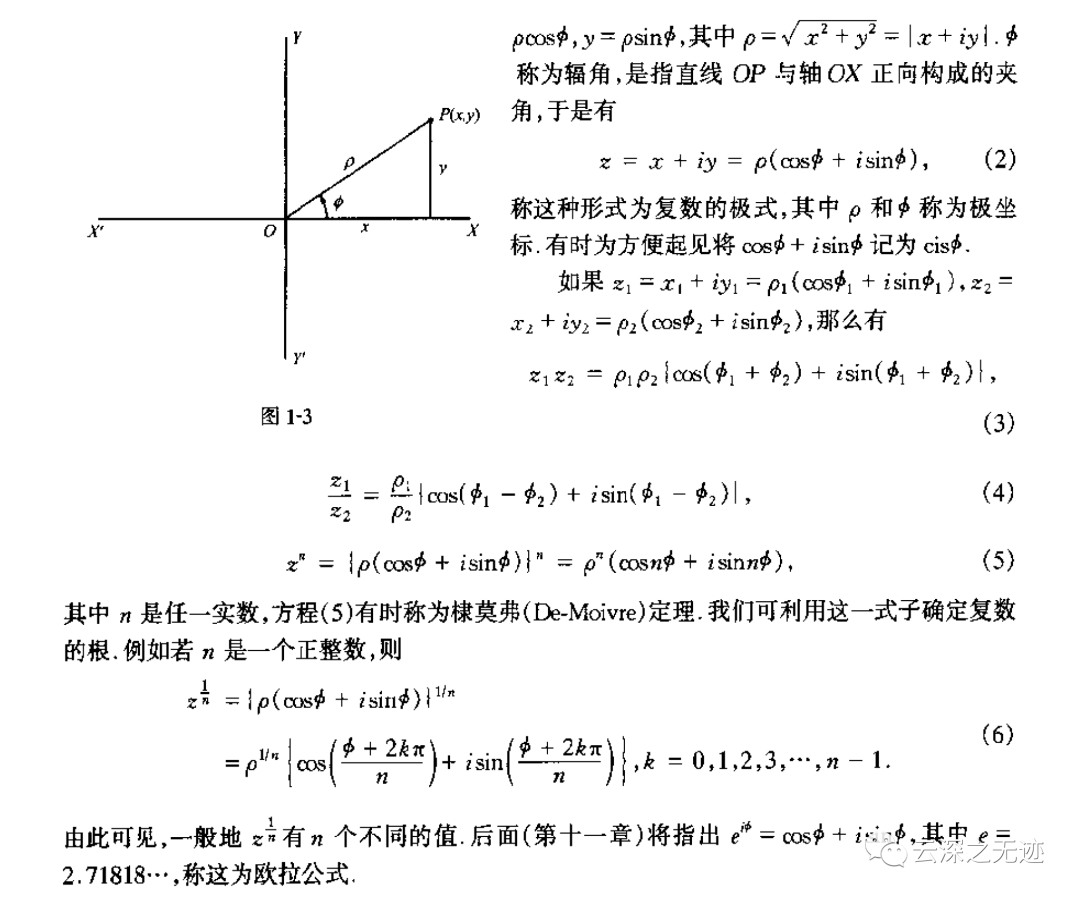
内容也很好，推荐一读

按照我老师的说法，我的理论已经ok了，所以要拉我去做题，emmmm。

这个我不用多说吧？？？

事实上，这次要讲的确实是求导，但是比哪个东西高级。

在微积分中，牛顿法是一种迭代方法，用于求可微函数F的根，它是方程F （ x ） = 0的解。因此，牛顿法可以应用于二次可微函数f的导数f ‘以求导数的根（f ’（ x ） = 0的解），也称为f的临界点 。 这些解可能是最小值、最大值或鞍点。这与优化有关，优化旨在找到函数f的（全局）最小值。

优化的核心问题是函数的最小化。让我们首先考虑单变量函数的情况，即单个实变量的函数。

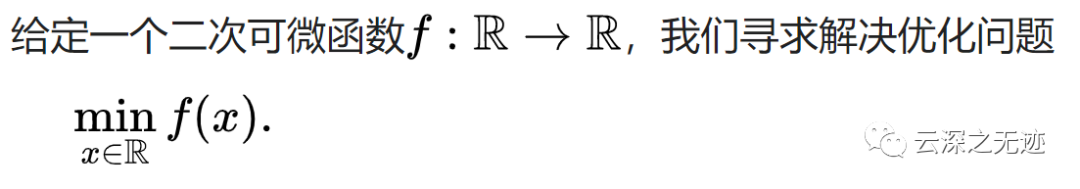
找最小

这是基本牛顿法：

理论是这样的

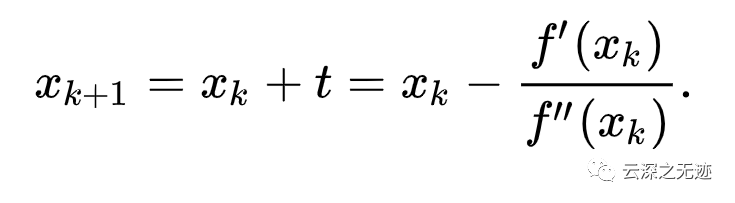
这是最终的更新公式

接下来再细讲，并不是所有的方程都有求根公式，或者求根公式很复杂，导致求解困难。利用牛顿法，可以迭代求解。

原理是利用泰勒公式，在x0处展开，且展开到一阶，即f（x） = f（x0）+（x－x0）f‘（x0）

求解方程f（x）=0，即f（x0）+（x-x0）*f’（x0）=0，求解x = x1=x0－f（x0）/f‘（x0），因为这是利用泰勒公式的一阶展开，f（x） = f（x0）+（x－x0）f’（x0）处并不是完全相等，而是近似相等，这里求得的x1并不能让f（x）=0，只能说f（x1）的值比f（x0）更接近f（x）=0，于是乎，迭代求解的想法就很自然了，可以进而推出x（n+1）=x（n）－f（x（n））/f‘（x（n）），通过迭代，这个式子必然在f（x*）=0的时候收敛。整个过程如下图：

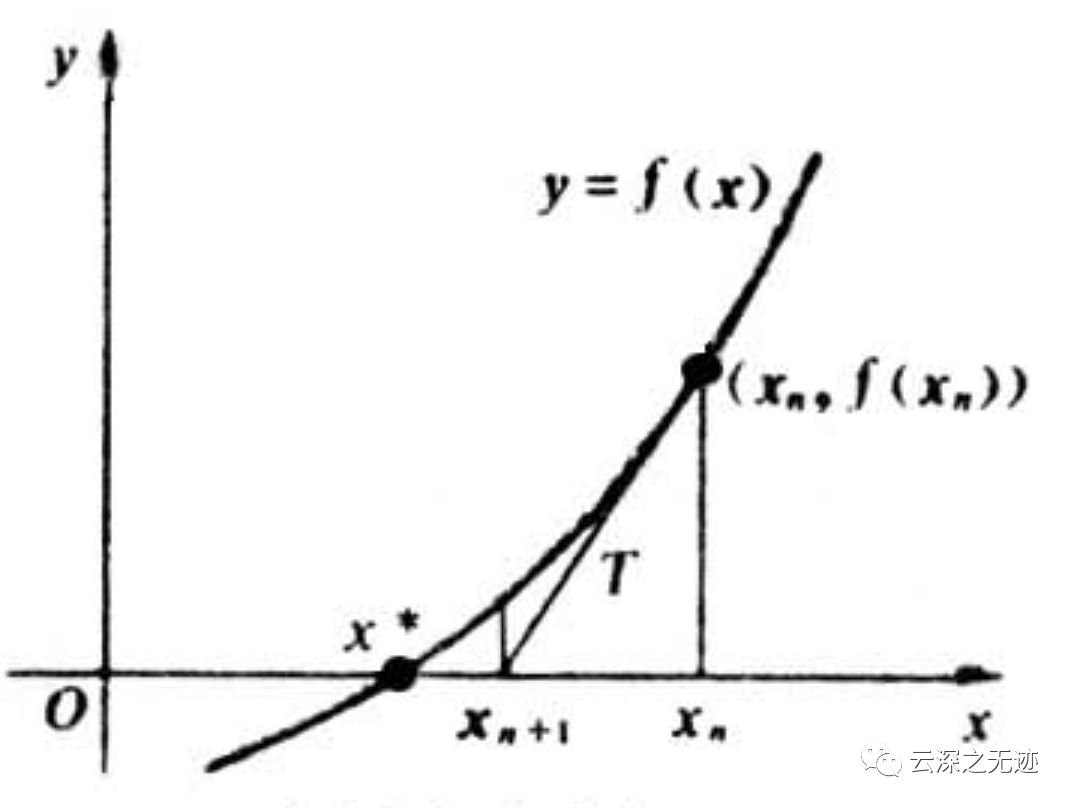
这是求根

接下来是最优化，对一个目标函数f，求函数f的极大极小问题，可以转化为求解函数f的导数f’=0的问题，这样求可以把优化问题看成方程求解问题（f‘=0）。

剩下的问题就和第一部分提到的牛顿法求解很相似了。为了求解f’=0的根，把f（x）的泰勒展开，展开到2阶形式：

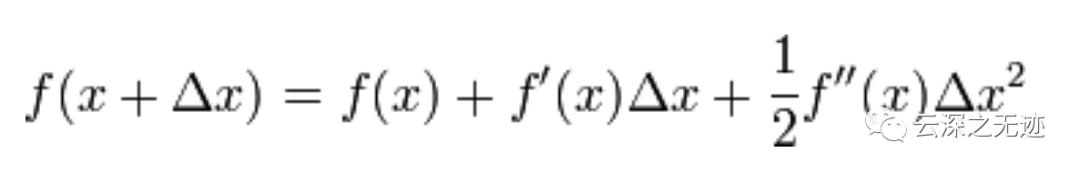
当且小三角无限趋于0 的时候

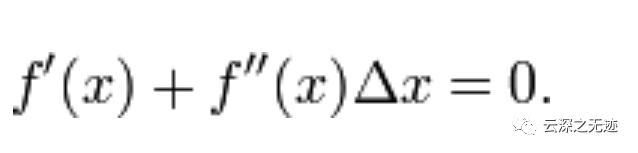
这个成立

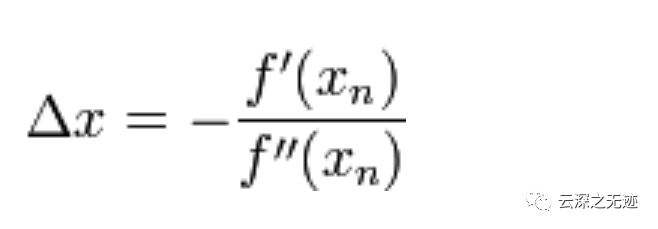
我们的最终迭代公式就出来了

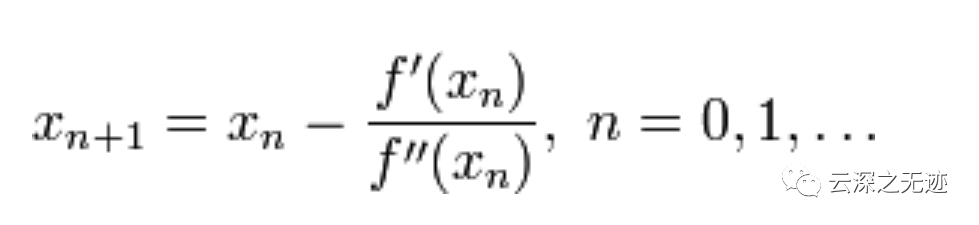
值得更新公式

牛顿法用于函数最优化求解”中对函数二阶泰勒公式展开求最优值的方法称为：Newton法，

牛顿法用于方程求解”中对函数一阶泰勒展开求零点的方法称为：Guass-Newton（高斯牛顿）法。

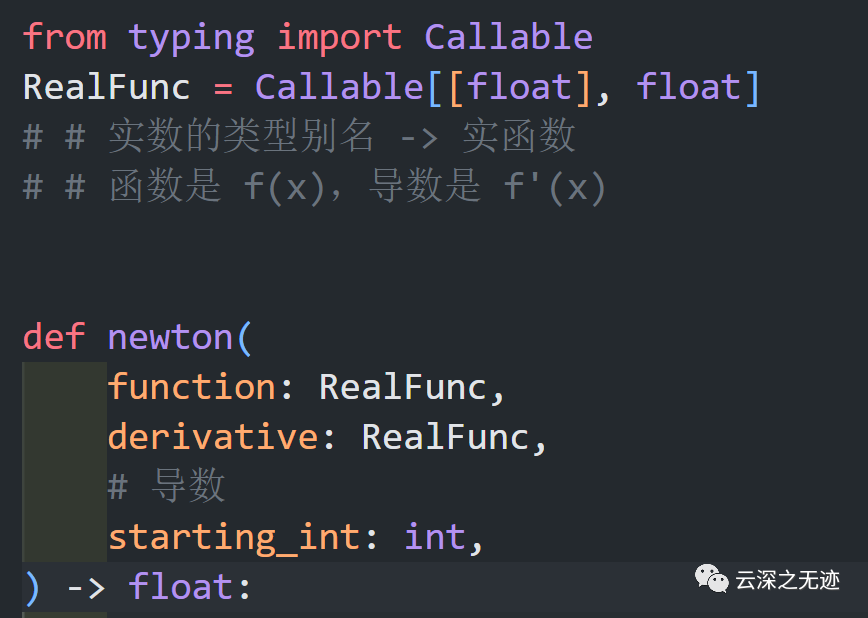
这次得比较难。。。就提前写好求导：

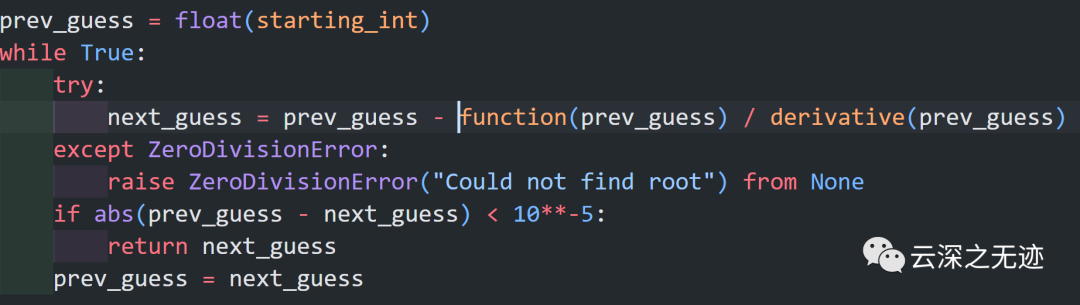
这个公式就是上面的更新公式

我们提前把函数和求导的函数写好

原文标题：Python实现所有算法-牛顿优化法

文章出处：【微信公众号：云深之无迹】欢迎添加关注！文章转载请注明出处。　　

      审核编辑：彭静