如何去实现一种比特对编码乘法器的设计呢

比特对编码与比特对编码乘法器的设计

今天一起看看比特对编码（有的也把它称为基4booth编码，名字不重要，主要是思想），可以解决上文中提到的问题

比特对编码原理

booth重编码的主要问题在于不能过滤掉010这样序列。故考虑将通过连续相邻两位进行编码，每次从低位向高位移动1位的方式（即booth比编码），变成连续相邻3位进行编码，每次从低位向高位移动2位的方式（比特对编码）。先讨论其原理。

一个数我们考虑从低位向高位对其进行编码，使其变成4进制（基4）的表示形式，每两位二进制表示一位的四进制数。

3（2'b11）比4少1，2(2'b10)比4少2。在4进制数中，2需要向前进位则需要减去2再向前进位；3需要向前进位则需要减去1再向前进位。

我们的比特对编码就是基于上述原理来的。

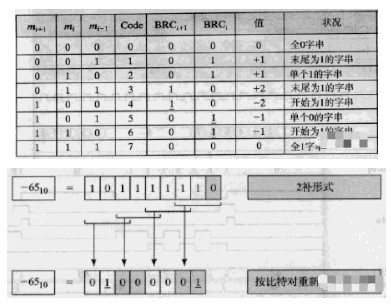
下面给出比特对编码规律，如下表和图所示，图为一个实例，是对1011_1111的编码，其表示-65。比特对编码结果为   -1 0 0 -1,故其表示的十进制d为：

d=-4^3 - 4^0 = -65

再举个例子，比如对  0001_1001进行比特对编码，得到编码为：

+2 -2 +1

故其表示的十进制计算如下：

d=2*(4^2) -2*(4^1) + 4^0 

= 32+8+1=41

其中的乘2与乘4都可以通过移位操作来实现，这就是为什么需要这么编码的原因。

可以看到，每相邻三位进行编码，其中的最低位mi-1 其实表示来自前面的进位。故当其为 001时，得到的编码为 +1(表示4)，011时最低位1表示进位，故编码为1+1=+2。

从中可以得出，对于8位二进制数0101_0101，经过比特对编码后，得到的是 +1 +1 +1 +1，其表示的数为：

4^3 + 4^2 + 4^1 + 4^0 = 

64+16+4+1=85

此时只需要进行3次加法运算，不会存在booth编码所存在的问题。

同时发现对于数据位宽非偶数的数，我们需要将其在最高位补填一位符号位，再进行比特对编码。

比特对编码（对乘数进行编码）乘法器，需要进行的加法次数为乘数位宽的一半。

比特对编码乘法器设计

设计思想概叙：定义位宽为DW_A+DW_B+2的product寄存器（DW_A为被乘数a的位宽，DW_B为乘数b的位宽）。当in_valid与in_ready同时为高时，将乘数b（位宽为b）加载到product的低DW_B位。然后在计算状态下（executing），将每次加法器的输出放到product的高位，并每个时钟周期将product右移2位。每个时钟周期，通过对

m={product[1:0],prd_r[1]}

（其中prd_r[1]为上一个时钟product的第二位）进行编码，得出本次操作是加1、加2，减1，减2，还是不用做加减法（编码为0）（代码中上述五种操作对应的标志信号分别为add_1,add_2,sub_1,sub_2，noneed_add）。并将加法结果每次存到product寄存器的高位。

这里有个巧妙的思想就是，每个时钟周期通过对product右移2位，再将其高DW_A位与a或者a*2进行相加或者相减操作，正好相当于每次product不动，把a或者a*2左移2位（乘以4）。这个思想源于《Verilog HDL 高级数字设计》中的精简寄存器时序乘法器设计。

注意，这里是有符号数乘法器，每次左移需要在高位补符号位，故左移不能简单的用 >> 描述（>>左移默认高位填0），具体描述见代码。

其中减法采用加上这个数的补码的方式；通过一个计数器（cnt）来指示什么时候结束运算；其中运算控制状态机采用《状态机的第四种描述方式》编写；条件选择多采用与或方式实现。

设计Verilog如下（dff_with_en为寄存器）：

 

 

 

 

 

 

如果乘数b位宽为奇数，请补一位符号位，变成偶数位宽，再输入。

审核编辑：刘清