

网络分析仪的基础知识
电子说
描述
网络分析仪作为一款多功能测试测量仪器,在电子信息化高速发展的今天,已经越来越多地应用在各类领域,包括天线与RCS测试、元器件测试、材料测试等等。但是网络分析仪的使用也与传统示波器、万用表等仪器有较大的差异。下面这篇文章中我们将为大家介绍一些网络分析仪的基础知识。
在我们使用网络分析仪时,往往会遇到阻抗匹配的问题,那么什么是阻抗,阻抗匹配的理想模型是什么,又需要用到什么方法实现呢?在观察测试信号时,我们也会查看网络分析仪上各种不同的图表,而这些图表又该怎么查看以及代表什么意义呢?下面将为大家解答。
我们知道,电路是对电流有阻碍作用的,要想让电流从一端流到另一端一定要有电压差,电流经过电路也会发生一定的损耗。物理学上把电路中对电流所起的阻碍作用叫做阻抗,单位为欧姆,阻抗可分为电阻和电抗两个部分,用公式表示为:
Z= R+i( ωL–1/(ωC))
阻抗匹配
当两个阻抗不同的设备连接到一起进行信号传输时,连接处会发生信号反射,这会使信号衰减,无法达到完美传输的效果,此时就需要对设备进行阻抗匹配。阻抗匹配是输入端与输出端阻抗的相互匹配,使信号不会在连接处发生反射的一种传输状态。主要用于传输线上,让信号不会在连接处产生反射,减小传输线缆对高频信号的损耗,提升传输效率。
不同电路的阻抗匹配条件是不一样的。在纯电路中,当负载电阻等于输出源内阻时,此时的输出功率最大,这种工作状态称为匹配,否则称为失配。当输出源内阻和负载阻抗含有电抗成分时,为使负载得到最大的功率,负载阻抗与内阻必须满足共轭关系,即电阻成相等,电抗成分只有数值相等而符号相反。这种匹配称为共轭匹配。
日常中用到的线缆阻抗大多数为50欧姆,所以阻抗匹配的最理想的模型是输出和输入端都为50欧姆,这样输出和输入端所构成的电路就不会发生过大的损耗。但是在实际测试中,往往会遇到各种情况,不可能都为50欧姆,这个时候,我们就需要使用电容和电感来进行阻抗匹配,达到RF性能最优。
目前,阻抗匹配的方法有很多,主要包括计算机仿真计算、手工计算、经验推测以及最常用的史密斯圆图。计算机仿真操作复杂,需要足够多的测试数据和设备支持,不能马上得出结果;手工计算相比于计算机仿真更为费时,在计算机普及的现在,已经被计算机所取代。有些射频经验比较丰富的工程师可以利用经验进行大致判断,但是不够准确,而且不是人人都能进行正确的判断,那么什么方法既快速准确,又相对简单呢?答案是史密斯(Smith)圆图。
史密斯圆图
在史密斯圆图发明之前,进行阻抗匹配需要花费很大功夫,当时在美国RCA公司工作的菲利普·史密斯(Phillip Smith)就考虑:能不能以一种简单的图表表现复杂的函数计算式,这样结果可以直接由图表来呈现出来,不用再耗费大量的人力和时间去计算大量的函数计算式。于是,1939年,一种能够以图表形式呈现函数表达式的图被发明了出来,这个图形通俗易懂、查看便捷,而后迅速在相关领域取代了原有的复杂计算方法,这就是后来人们所称的史密斯圆图。
史密斯圆图主要基于以下算式:
Γ= (Z - 1)/(Z+ 1)
Γ代表其线路的反射系数(reflection coefficient),即S-parameter里的S11;Z是归一负载值,即ZL/Z0,其中,ZL是线路的负载值,Z0是传输线的特征阻抗值,通常会使用50Ω。用图表示为:
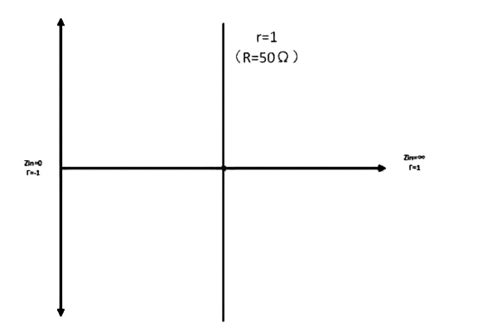
现在看到的图像和我们平时看的图表一样,是横平竖直的坐标线,与复杂的史密斯圆图有非常大的区别,但是当我们把纵坐标弯曲起来,就得到了另一个图形。
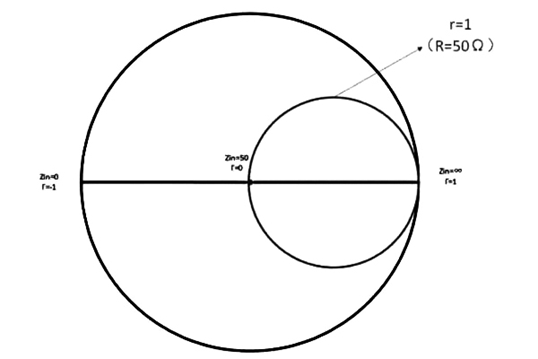
这看起来和我们常见的史密斯图有点像了,但是好像太简单了,那么如果在正常坐标里面再加两条线呢?
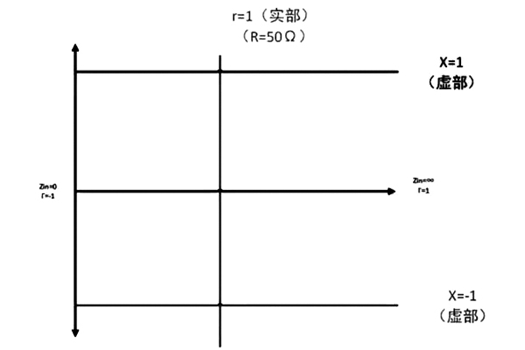
在加入X=±1两条线后,按照原来的方法令图表弯曲,就得到下图:
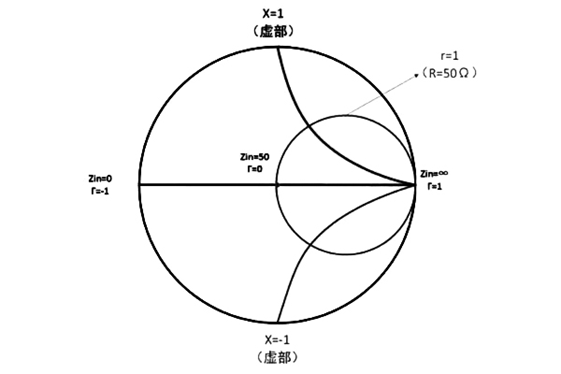
这样看起来已经比较接近我们熟悉的史密斯图了,差不多是一个高中水准的图表。在这个图表中,我们已经能简单的判断一些特性,比如:最大的圆上的点阻抗实部为0,小圆上的点实部为1,也就是电阻为50欧姆。通过分析我们就可以得出,上半圆区域为感性区域,虚部为正;下半区域为容性区域,虚部为负等等。
当我们再把图表精细化,加入更多的横线与竖线,就可以得到一个非常复杂的图像:
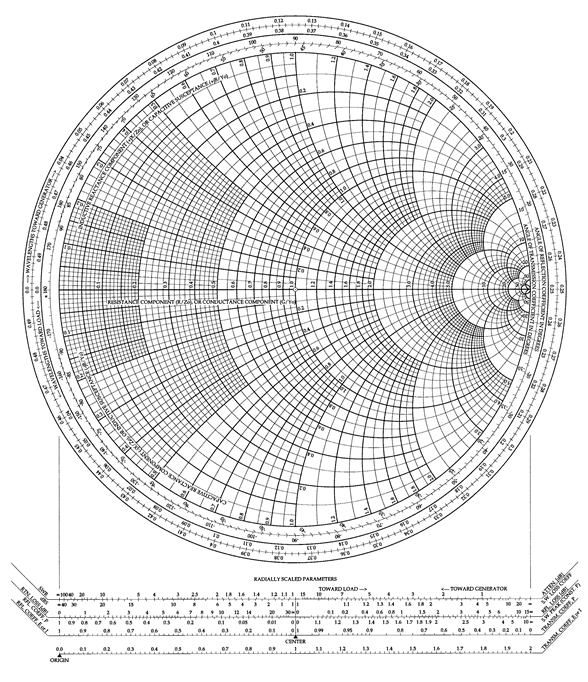
上图就是比较完整的史密斯圆图,我们可以查看到相当多的信息,但是从高中一下跳到研究生未免跨度太大,看着这个图像是不是一头雾水呢?现实中可能用不上这么精密,所以可以将图片简化,去掉一些细分的曲线,得到下图:
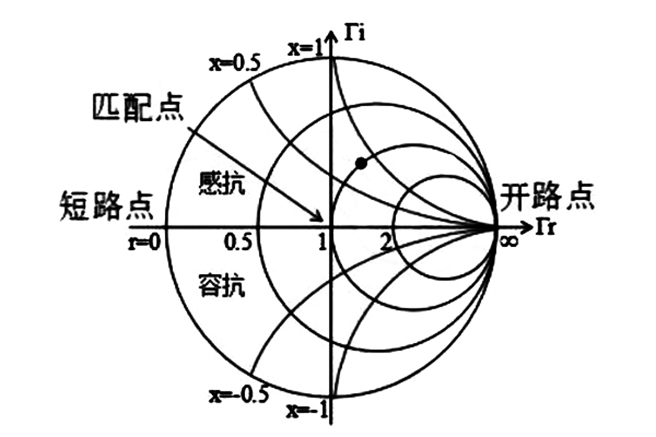
这个图像是我们日常中见得比较多的样子,也是大多数仪器中史密斯圆图的表现形式,这样既能清晰的查看信号,也不会由于过于复杂而令使用者晕头转向。现在以这个圆图做一个简单的总结,了解图形的特性:
圆的上半部分是感抗,虚部为正;下半部分是容抗,虚部为负;
r=o上的圆:实部为0(电阻为0);
r=1上的圆:实部为1(电阻值为50欧姆);
r=0到r=∞这条线:虚部为0(电感,电容为0);
圆心的位置就是匹配点,左右两侧圆的切点分别为短路点和开路点。
通过上述分析可以知道,史密斯圆图不但能让我们更快速地进行阻抗匹配,同时,作为网络分析仪中一个最常用的显示界面,史密斯圆图让我们可以在使用网络分析仪时看懂所测信号的特性。
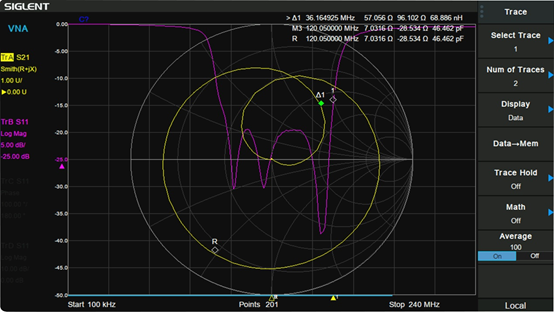
△ SVA1000X系列史密斯圆图
上方的图为SVA1000X网络分析仪的史密斯测试图,紫色的线是S11测试迹线,为正常的损耗曲线,黄色的迹线为史密斯图曲线。结合前面的分析,我们可以发现,这个测试器件的特性非常特殊,起始点都在圆心,阻值为50欧,曲线围成了一个圆形,是阻值不变的情况下,电抗部分随着频率在感性与容性之间变化导致的。
审核编辑 :李倩
-
可以使用信号分析仪作为网络分析仪吗?2019-06-24 0
-
网络分析仪基础知识2019-09-05 0
-
矢量网络分析仪使用教程2011-09-19 5742
-
网络分析仪基础2012-01-17 1586
-
矢量网络分析仪基础知识及S参数测量2012-03-30 1062
-
网络分析仪的原理及应用2017-11-23 2964
-
看图了解矢量网络分析仪基础知识要点2017-12-22 9411
-
网络分析与网络分析仪的详解2018-05-02 24927
-
矢量网络分析仪的基础知识和参数测量的详细资料合集2020-01-07 672
-
网络分析仪校准的基础知识2022-08-10 3275
-
新手应该了解的网络分析仪的基础知识2022-11-07 2633
-
网络分析仪测量阻抗匹配的工作原理2022-12-28 3591
-
什么是矢量网络分析仪?矢量网络分析仪的误差类型有哪些?2023-03-02 2434
-
网络分析仪的分类2024-05-08 634
-
网络分析仪工作原理 网络分析仪和频谱分析仪的区别2024-06-03 1669
全部0条评论

快来发表一下你的评论吧 !

