使用统计数据来进行示波器数据分析

示波器通过测量产生的大量数据可以做出惊人的事情。您的示波器可以让您“看穿”噪声并降低测量不确定性。魔术是通过应用于大型数据集的统计数据来实现的。虽然某些处理，如直方图，显然是基于统计的，但有些统计是隐藏的。无论哪种情况，您都可以利用示波器的统计分析。

考虑一个基本的示波器测量噪声方波，如图 1 所示。

 

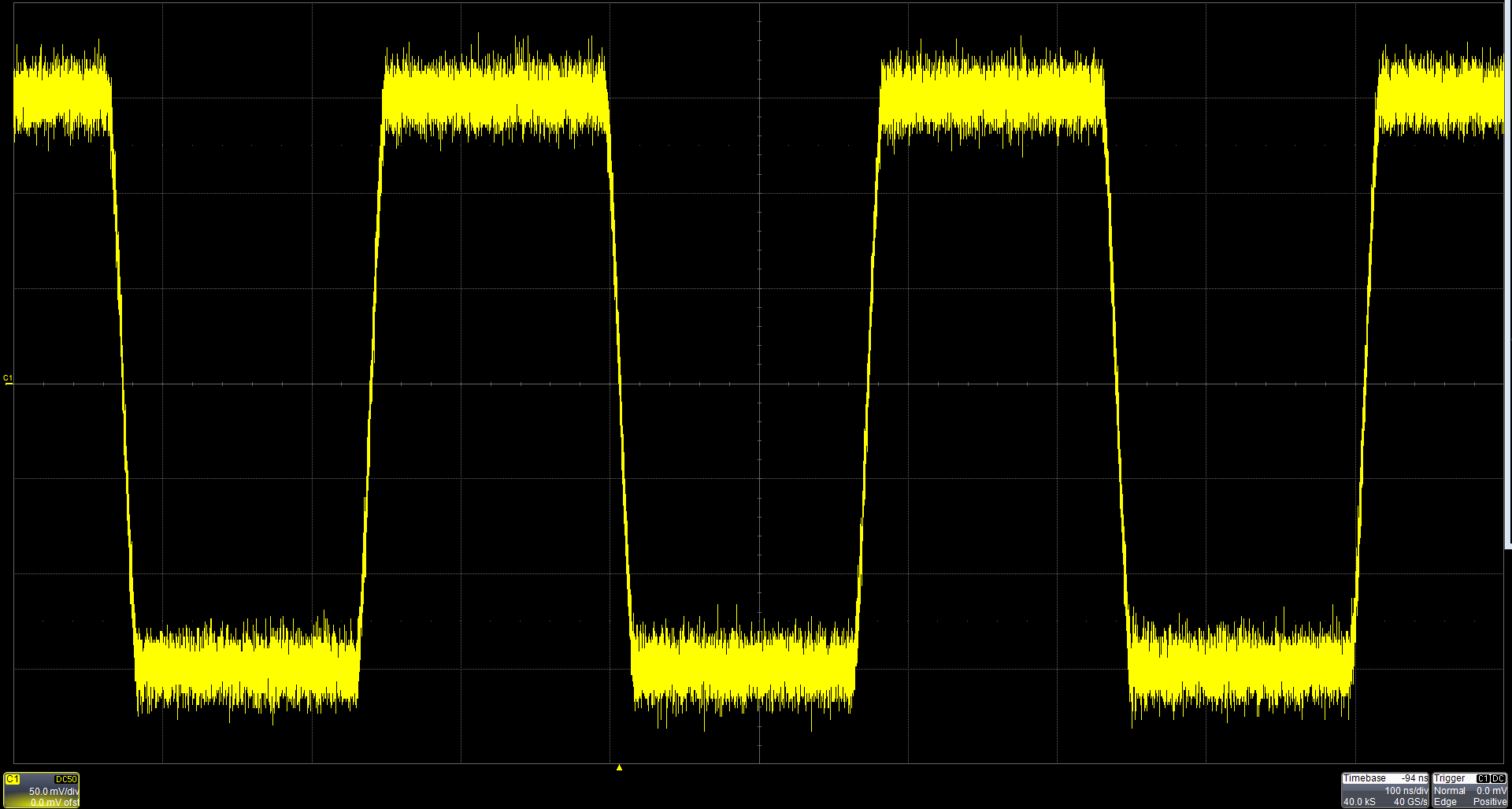
图 1. 方波上的噪声增加了寻找信号幅度的难度。

方波上的噪声使得测量其幅度变得困难。幅度构成其他测量的基础，例如宽度、上升时间、下降时间、过冲，甚至在某种程度上频率和周期。例如，上升时间测量是信号从其幅度的 10% 变化到 90% 所需的时间。宽度是在信号幅度的 50% 处具有相反斜率的转换之间的时间差。因此，确定幅度对于几乎所有其他测量都至关重要。

平均

几乎所有示波器都提供平均功能，这是应用于波形的最常见的统计过程。采集多个波形并将它们逐点相加，然后将总和除以平均值中的波形数，得出波形的平均值或平均值，如图 2 所示。上面的轨迹是采集的波形。较低的迹线是一千次采集的平均值。平均抑制了噪声，留下了干净的波形。

 

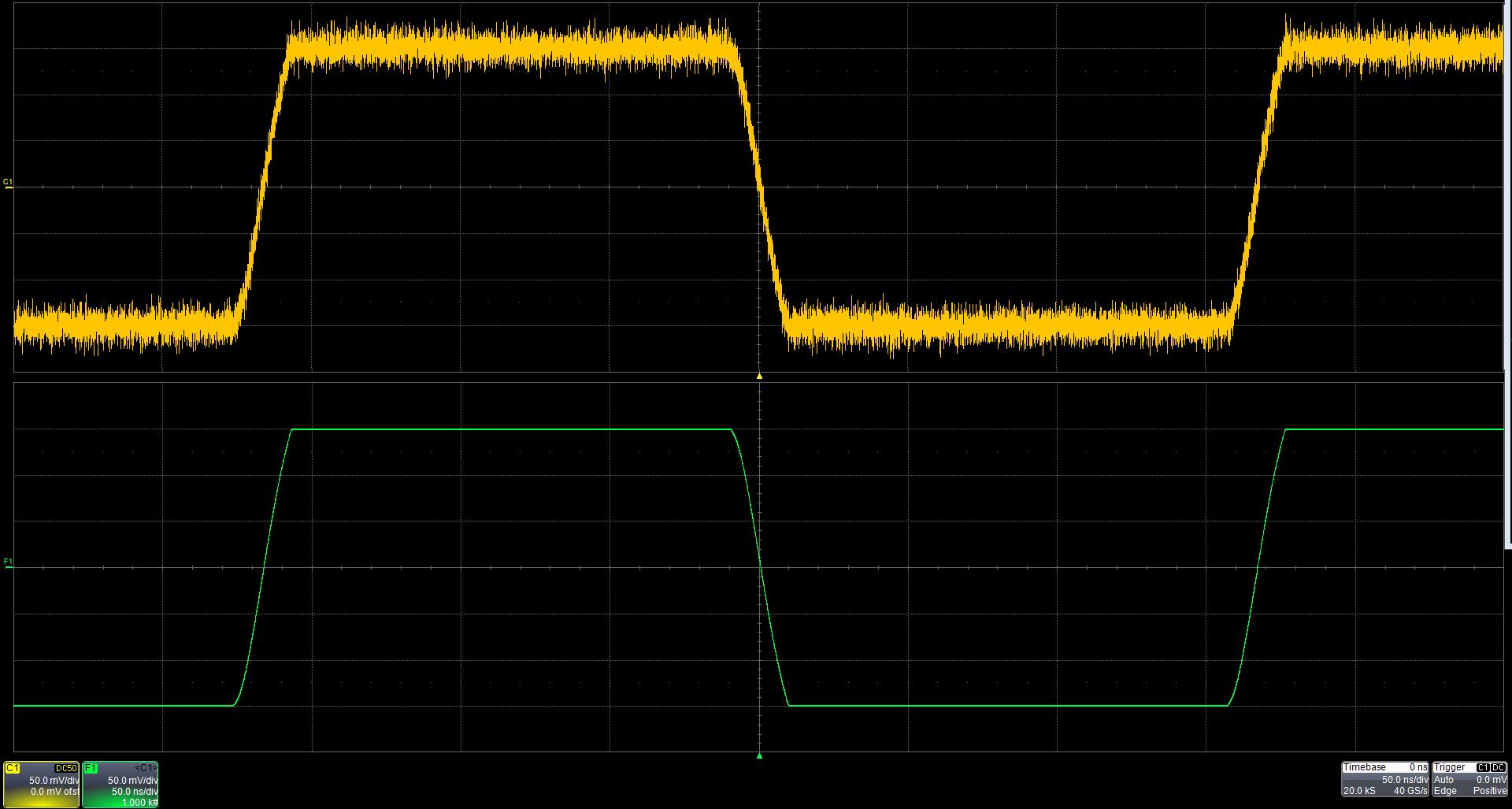
图 2. 平均将多个波形相加，并通过采集的波形数量对总和进行归一化，从而降低噪声。

对于高斯分布噪声，噪声幅度随着平均波形数的平方根而减小。因此，一千个采集的波形将噪声幅度分量降低了 31.6 倍或约 30 dB。平均过程的唯一缺点是需要采集大量波形。

另一种统计方法

统计数据也可以量化不确定性。如果使用方波的每个样本值来创建其瞬时幅度值的直方图，您可以开始看到我们波形的结构，如图 3 中的复合图形所示。直方图是生成的，经过旋转使其幅度刻度垂直以匹配采集的波形，然后叠加在信号波形上。

 

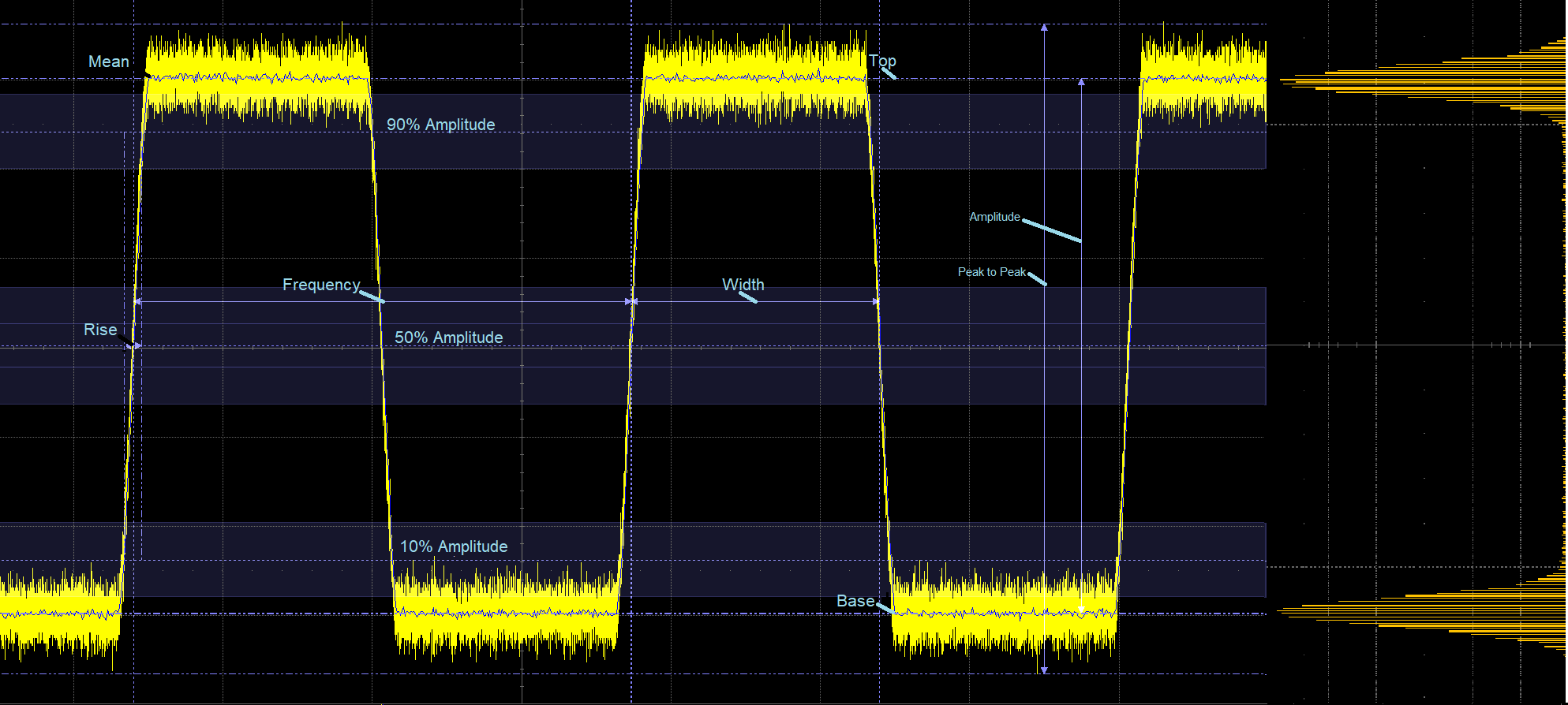
图 3. 生成直方图后，我旋转它使其与波形的顶部和底部幅度对齐。这样做会产生信号的幅度，即使在低信噪比的情况下也是如此。

直方图有两个峰值。一个对应于方波的最高电平，称为顶部，而另一个对应于较低电平或基值。各个直方图元素的平均值表示顶部和底部值。方波的幅度是顶部和底部幅度之差。知道幅度可以计算所有其他脉冲参数，如图 2 所示。统计数据让您可以看穿数据的随机部分，从混沌噪声效应中提取有意义的信息。该技术适用于单次采集，不需要多次采集。然而，多次采集确实提高了测量的准确性。

测量统计

当应用于示波器测量参数时，可以使用统计数据。统计数据可应用于示波器中可用的任何测量参数。图 4 是测量时钟信号的时间间隔误差 (TIE) 的示例。

 

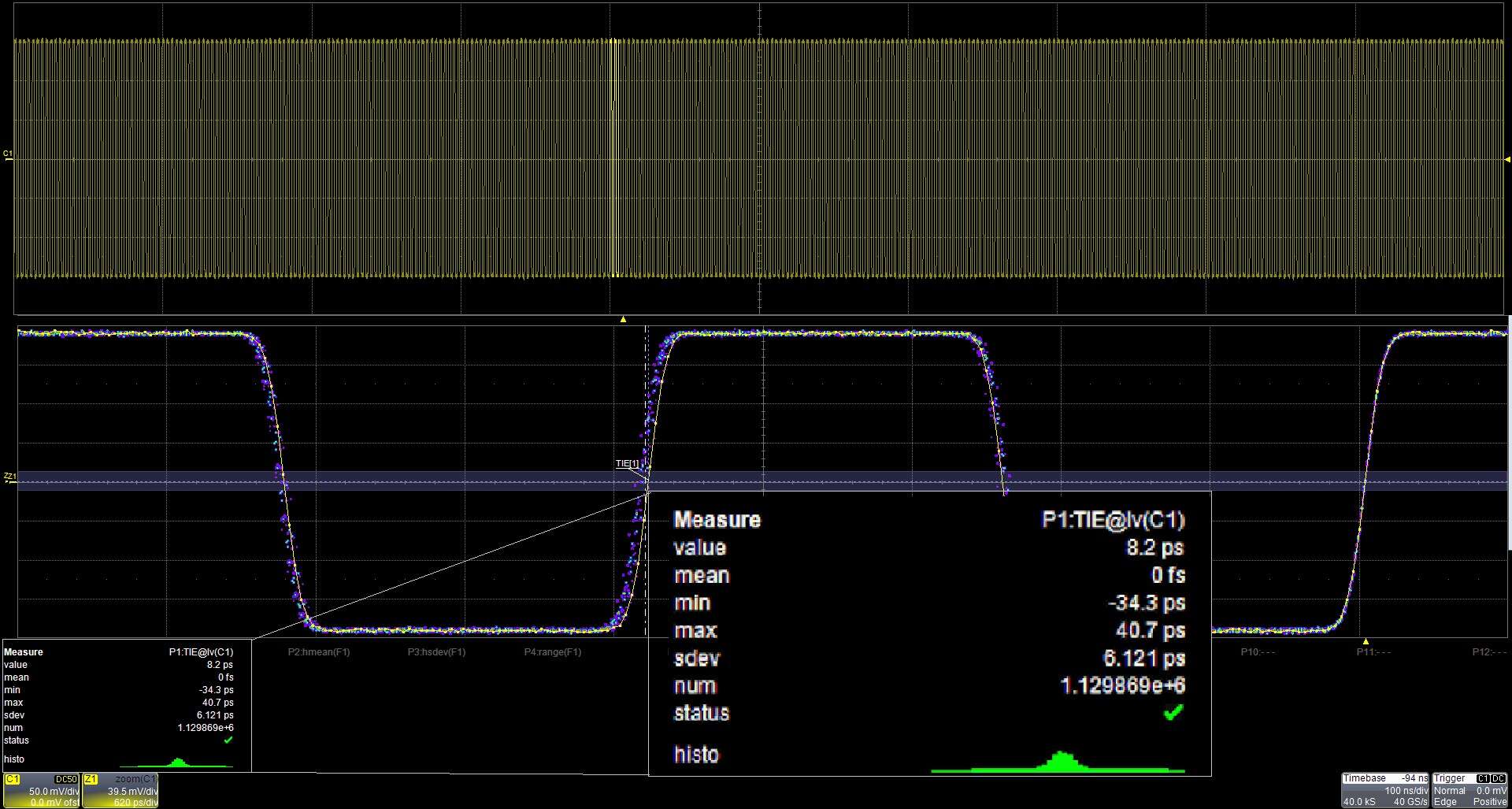
图 4. 333 MHz 时钟的 TIE 测量，测量统计包括平均值、最小值 (min)、最大值 (max)、标准偏差 (SDEV) 以及统计中包含的测量次数。

图 4 的上部轨迹。显示 333-MHz 时钟信号，而下部轨迹是水平扩展轨迹的放大图。TIE 是获取的边缘与其理想时间位置之间的时间差的度量。将其视为信号的瞬时相位。示波器对采集波形的每个边沿执行 TIE 测量，即所谓的“所有实例”测量。测量读数字段已扩展，使其更易于阅读。测量读数显示最后一次 TIE 测量值，在本例中为 8.2 ps。它还显示统计值中包含的平均值、最小值、最大值、标准偏差和测量次数。

在这种情况下，统计数据包括超过一百万个值。平均值是所有这些测量值的平均值，在这种情况下为零。由于 TIE 的值不为零，这表明 TIE 测量值既有正值又有负值，平均为零。最小值是确定的最低 TIE 值，最大值是遇到的最大 TIE 值。最大值和最小值之差是测量的统计范围。在示例中，最小值为 -34.3 ps，最大值为 40.7 ps，这同时确认了正值和负值。标准差，通常称为 sigma，是样本值关于平均值分布的量度。由于平均值为零，因此标准偏差等于 TIE 的均方根 (rms) 值。

在数值测量读数下方是一个标志性的直方图，称为“直方图”，它显示了测量值的分布。直方图绘制了值在小范围或 bin 内的样本数量与值的关系。“histicon”的钟形分布是高斯或正态分布的特征。

测量统计数据提供了百万次测量的简明描述。我们知道平均值，最大和最小测量值，以及呈高斯分布的直方图分布形状。

您可以更详细地轻松查看 TIE 测量的直方图。单击“histicon”将打开一个包含直方图的数学轨迹，以便进行更仔细的分析，如图 5 所示。

 

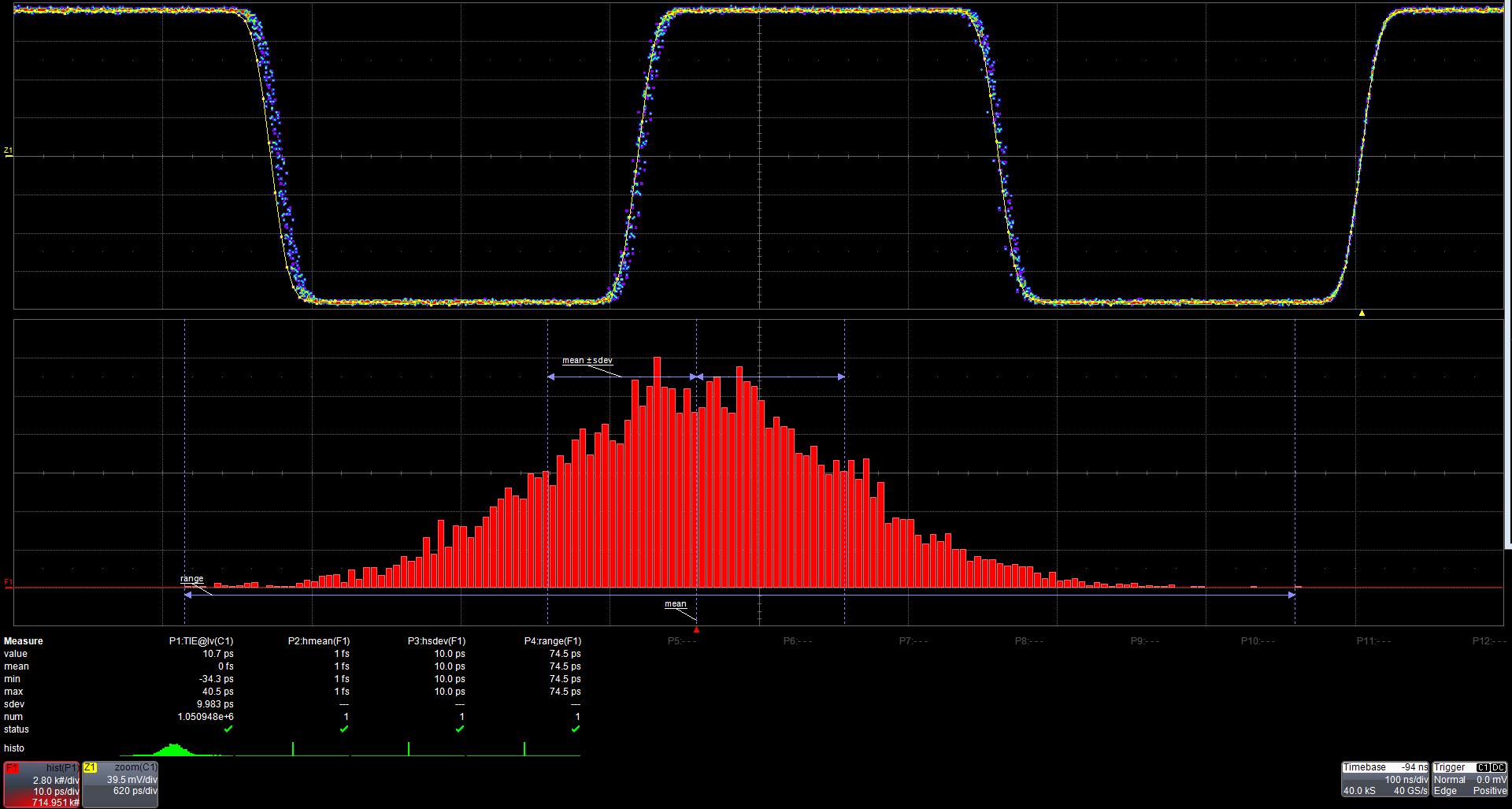
图 5. 展开“直方图”可以让您研究 TIE 测量的直方图。直方图参数读取平均值、标准差和范围。

迹线 F1 显示 TIE 测量值的直方图。直方图可以作为测量来源，并且启用了三个直方图参数来显示直方图的平均值、标准偏差和范围。参数标记以图形方式显示直方图参数基础。直方图并非在所有示波器中都可用，在大多数情况下，它是一个可选功能。

TIE 表示时序不确定性或抖动的一种形式。直方图参数量化了抖动读数。标准偏差是 rms 抖动，范围参数代表峰间抖动。这些值测量直方图中包含的值数量的实际抖动。此信息可外推以将抖动值投影到 10 12 或更多值。这是为许多高速串行数据标准所需的抖动测试而完成的，大多数高端示波器都提供此类串行数据分析选项。

 

审核编辑 黄昊宇