

用于计算接收器灵敏度的每个构建块特性
描述
介绍
接收器通常包含窄带通硬件滤波器以及在数字信号处理 (DSP) 中实现的窄低通滤波器。等效噪声带宽 (ENBW) 是了解这些滤波器中存在的本底噪声的一种方式。要预测接收器设计的灵敏度,了解包括 ENBW 在内的噪声至关重要。本文将介绍用于计算接收器灵敏度的每个构建块特性,然后将它们放在一起进行计算。
接收灵敏度
接收器灵敏度是衡量接收器从微弱信号中解调和获取信息的能力。我们将灵敏度量化为可以从中获得有用信息的最低信号功率水平。在模拟 FM 系统中,可用信息的标准品质因数是 SINAD,即解调音频信噪比。在数字系统中,接收信号质量是通过计算接收到的错误比特与接收到的总比特数的比率来衡量的。这称为误码率 (BER)。大多数陆地移动无线电系统使用这些品质因数之一来量化灵敏度。为了测量灵敏度,我们应用所需信号并降低信号功率,直到达到质量阈值。
SINAD
SINAD 是用于信噪比和失真比的术语,是一种音频信噪比。在模拟 FM 系统中,解调的音频信噪比是射频信号质量的指标。为了测量音频信噪比,通常测试设备测量总音频功率(信号加噪声加失真),然后对音频信号音调进行陷波滤波(通常为 1 kHz)并再次测量音频功率(噪声加失真)和以分贝为单位。
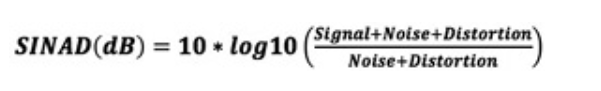
陆地移动无线电行业标准通常使用 12 dB SINAD 来测量参考灵敏度。
误码率
误码率是数字调制系统中信噪比的量度。为了计算 BER,必须将已知的重复模式传输到无线电。接收器必须解调数据并将其与已知数据模式进行比较,并确定错误的位数。BER 是错误比特与接收到的总比特的比率。陆地移动无线电的行业标准通常为 5% 的参考灵敏度 BER。
计算接收器灵敏度
如果知道以下性能参数,则可以计算接收器的灵敏度:噪声系数 (NF)、ENBW 和实现所需质量信号所需的载噪比 (C/N)。
灵敏度如下:
灵敏度=10×log10(kTB)+NF+C⁄N
该等式定义了解调器中存在的信号功率,单位为 dB·Watts,以获得所需的载噪比。让我们解释这个等式中的每个术语。
什么是“kTB”?
总热噪声功率 (kTB) 是三个量的函数:1) 玻尔兹曼常数“k”,单位为焦耳/°K,2) 温度,单位为°开尔文,以及 3) 接收器中通道选择性滤波的总带宽。由于对温度的依赖性,这被称为“热噪声”。
本底热噪声=k(Joules⁄˚K)×T(˚K)×B(Hz)
产生的噪声以焦耳/秒或瓦特为单位。要将噪声功率转换为 dB·Watts,请使用 10 倍的噪声功率对数(以瓦特为单位)。如果我们查看归一化(B = 1 Hz 带宽)本底噪声方程,我们有:
本底噪声=10×log10(k×T×B)
=10×log10(1.38×〖10-23×290˚×1 Hz)
= -203.9 分贝/赫兹
接下来,要将 dBWatts 转换为 dBmilliwatts (dBm),请将此值增加 30 dB:
–203.9 dBW/Hz+30 dB= -173.9 dBm/Hz
这是 1 Hz 带宽中的噪声功率量。
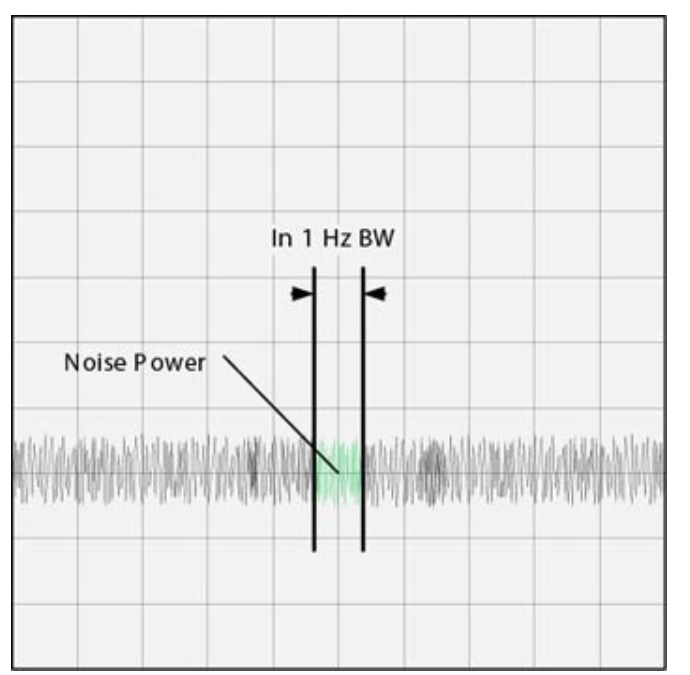
图 1 • 1 Hz 带宽内的噪声功率。
什么是噪声系数?
噪声系数是接收器中的电子电路添加到接收器输入的热噪声功率的噪声功率量。接收器输入端的热噪声通过解调器。这种噪声存在于接收通道中,无法消除。接收器中电路(例如放大器和混频器)的噪声系数会给接收通道增加额外的噪声。这会提高解调器的本底噪声。
什么是载噪比 (C/N)?
为了获得所需的解调信号质量,信号功率必须高于本底噪声。对于某些类型的调制,所需的信号功率与本底噪声的比率是已知的。对于使用 25 kHz 频道的模拟 FM 陆地移动无线电系统,接收器的信号功率必须比噪声功率高约 4 dB。这表示载噪比为 4 dB。
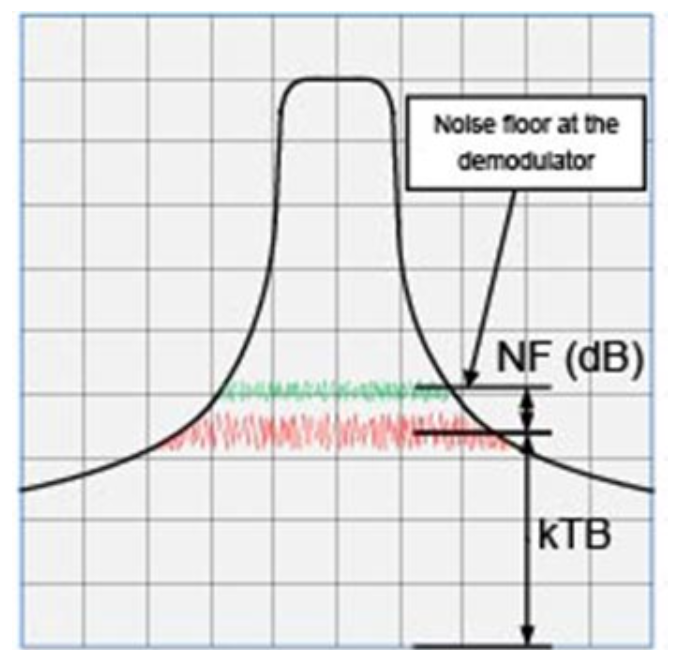
图 2 • 噪声系数添加到热噪声 (kTB)。
误码率 (BER) 是数字调制系统的灵敏度基准。Eb/No 是每比特能量 (Eb) 与噪声频谱密度的比值(No - 以 1 Hz 为单位的噪声功率)。某个 BER 所需的载噪比是信号 Eb/No 的函数。这是信噪比的数字系统表示。每种数字调制类型都有一条 Eb/No 曲线(Eb/No vs. BER)。为了确定灵敏度,使用适当的曲线并找到所需的误码率以确定必要的 Eb/No。然后通过以下关系计算载噪比:
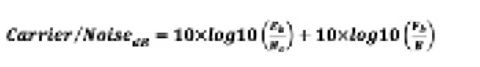
其中 Fb 是比特率,B 是接收器等效噪声带宽。
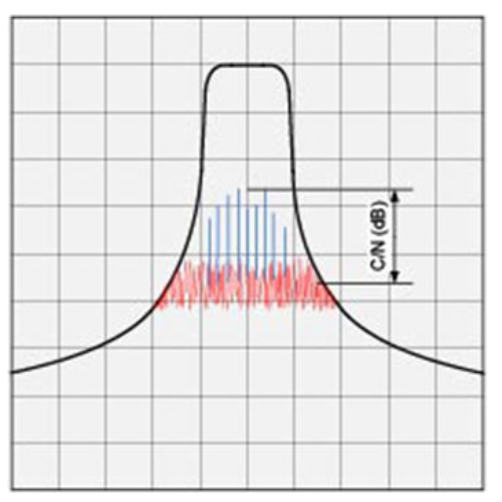
图 3 • 载噪比。
什么是等效噪声带宽?
滤波器的等效噪声带宽 (ENBW) 定义为完美矩形滤波器的带宽,该滤波器通过的功率量与接收器中通道选择滤波器的累积带宽相同。
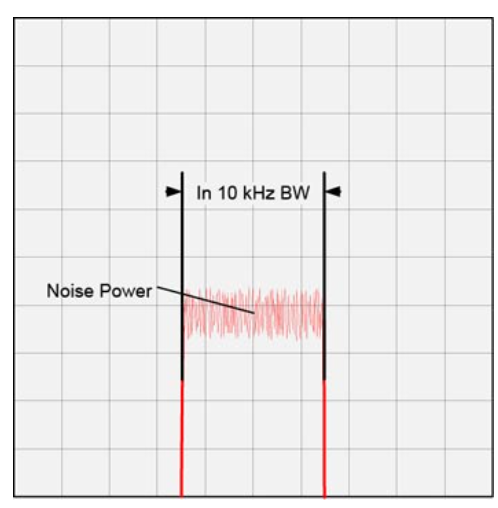
图 4 • 中频带宽中的噪声功率。
在这一点上,我们想知道接收器中的本底噪声,即来自 kTB 的接收器中频 (IF) 滤波器带宽中的噪声功率。由于 kTB 的单位是瓦特/赫兹,因此通过将 1 Hz 带宽中的噪声功率乘以以赫兹为单位的整体等效噪声带宽来计算通道带宽中的本底噪声。对于具有 10 kHz ENBW 的接收器,我们以 dB 毫瓦 (dBm) 为单位计算本底噪声,如下所示:
本底噪声=10×log10(1.38×〖10-23×290˚×1 Hz×10000)+30 = –134.0 dBm
接下来我们看看完美矩形滤波器的带宽如何与接收机中通道选择滤波器的实际滤波器响应进行比较。
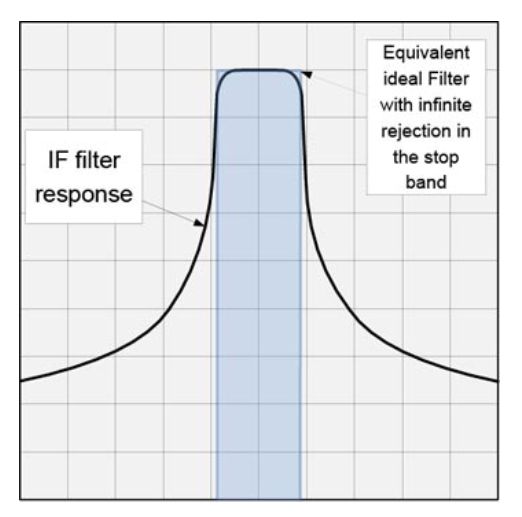
图 5 • 通过相同功率的完美滤波器。
我们使用等效理想矩形滤波器 (ENBW) 的带宽来计算热噪底。我们可以出于设计目的指定等效噪声带宽,但实际上,它是解调器前面所有滤波器的合成带宽。滤波器可以通过的功率是滤波器曲线下面积的函数。滤波器图以 dB 为单位。
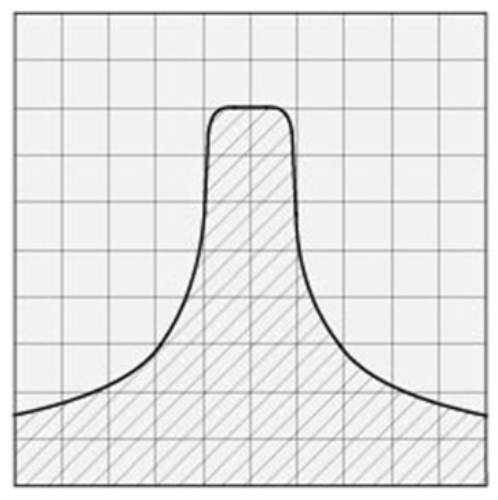
图 6 • 过滤器响应下的区域。
从测量数据计算 ENBW
理想情况下,我们通过积分从 -infinity 到无穷大的归一化滤波器功率频率响应曲线来计算 2 边 ENBW(对于以 fs 速率采样的数字滤波器,–fs/2 到 fs/2)。出于实际目的,归一化滤波器响应的 -60 dB BW 值可用作积分限制。由于我们正在寻找以赫兹为单位的带宽,因此我们不需要知道曲线下的绝对功率。积分必须以瓦特或毫瓦而不是 dB 的线性形式进行。散射参数或 S 参数是对射频 (RF) 电压如何通过射频网络传播的测量。使用网络分析仪可以轻松测量 RF 滤波器的 S 参数。然后我们使用测量的 S 参数数据计算带宽。由于 S 参数是与电压相关的测量,因此

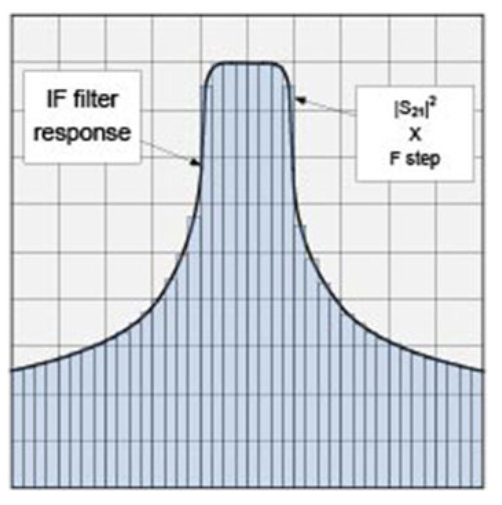
图 7 • 通过矩形求和进行积分。
我们可以使用直通响应 (S21) 的幅度作为电压项,并将阻抗归一化为 1 欧姆,以代入功率方程。这将给我们一个线性幂项。对于我们的例子,我们选择 S 参数,其中幅度以 dB 为单位。为了我们的计算,必须将功率转换为线性项。
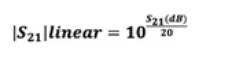
对于整体 ENBW,我们想要一个矩形,其中矩形的高度等于最大功率 (|S21|2)。矩形滤波器的面积等于滤波器曲线下的面积。使用均匀矩形的数值积分计算 IF 滤波器响应曲线下的面积。
通过将 |S21|2(幂)乘以 S 参数数据中使用的频率步长,找到每个均匀矩形的面积。
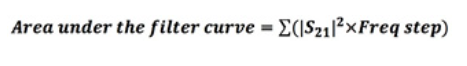
对于一个简单的矩形:
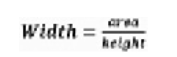
因此,ENBW 为:
因此,ENBW 为:
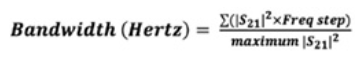
由于 S21 项是无单位的,我们现在得到一个以赫兹为单位的频率结果。结果是具有无限阻带抑制的矩形滤波器的带宽,它通过与我们测量的滤波器相同的功率(S 参数)。我们将在计算接收机本底噪声 (kTB) 时使用这个带宽。
我们可以使用软件来计算滤波器的 ENBW。
这是一个用于从“.s2p” s 参数数据文件计算 ENBW 的 Matlab 脚本:

图 8 • 使用 s 参数计算滤波器 ENBW 的 Matlab 代码。
有时,在 DSP 中实现为低通滤波器的数字滤波器是给定系统中最窄的滤波器。这是一个 Matlab 脚本,它将计算数字低通滤波器的 ENBW,给定一个包含滤波器抽头的文本文件:

图 9 • 使用 FIR 滤波器抽头计算滤波器 ENBW 的 Matlab 代码。
现在我们可以计算接收器灵敏度
我们有接收器灵敏度方程的每个元素的数量。为了计算接收器灵敏度,我们将接收器的整体噪声系数添加到本底噪声中。这量化了解调器输入端的本底噪声。信号必须比本底噪声高出所需信号质量所需的载噪比。当添加这些东西时,结果是满足称为参考灵敏度的可用信息的品质因数所需的功率水平。
灵敏度=10×log10(kTB)+30+NF+C/N
我们可以使用我们之前计算的 10 kHz ENBW 接收器中的本底噪声来计算具有 5 dB 噪声系数 (NF) 的接收器在 25 kHz 通道中模拟 FM 的灵敏度。在具有 10 kHz ENBW 的模拟 FM 接收器中,12 dB SINAD 所需的载噪比约为 4 dB。将值代入
灵敏度=10×log10(kTB)+30+NF+C/N
公式 10 如下:
灵敏度=10×log10(kT×10000)+30 dB+5 dB+4 dB
= –134.0 dBm+5 dB+4 dB
= –125.0 dBm
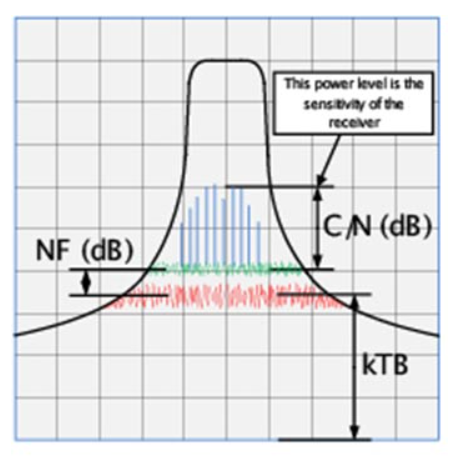
图 10 • 热噪声 (kTB) 加上 NF 加上 C/N。
结论
接收器的灵敏度是带限热噪声、接收器噪声系数和特定调制所需的载噪比的函数。等效噪声带宽是指噪声受频带限制的量。可以估计 ENBW,但可以根据测量数据或 DSP 滤波器抽头计算。利用这些特性,我们可以准确计算接收器的灵敏度。
关于作者:
Dennis Layne 是 Harris Corporation 的高级首席射频工程师。Dennis 拥有弗吉尼亚州林奇堡学院的物理学学士学位,并拥有 18 年的陆地移动无线电接收机设计经验。
审核编辑 :李倩
-
有什么方法能提高GPS接收器在同步GPS操作中的灵敏度?2019-08-22 2409
-
计算ASK接收机的灵敏度2008-09-17 1509
-
接收灵敏度的定义公式2009-04-25 15755
-
什么是接收灵敏度2009-05-08 4743
-
巨大的挑战:提高GPS接收器在同步GPS操作中的灵敏度2016-01-06 692
-
接收器灵敏度测试2016-01-11 8227
-
GPS接收器在GPS中的灵敏度提高设计2017-09-12 1261
-
如何提高GPS接收器在同步GPS操作中的灵敏度2017-11-24 1668
-
如何才能提高GPS接收器在同步GPS操作中的灵敏度2020-08-18 1130
-
如何提高GPS接收器的灵敏度2021-04-17 6172
-
设计解决方案44-高灵敏度接收器应用受益于16位130 Msps ADC的独特功能2021-05-16 720
-
如何测量接收器RF灵敏度2021-10-28 9700
-
扩频系统的接收器灵敏度方程2023-02-23 3251
-
利用外部LNA提高接收器灵敏度2023-02-24 3168
-
计算ASK接收器的灵敏度2023-03-02 2065
全部0条评论

快来发表一下你的评论吧 !

