

聊一聊向量到底有什么用
描述
既有大小又有方向的量,称为向量,同学们在学习这一部分数学知识时,似乎感到困惑:向量到底有什么用?今天,小编就和大家来聊一聊向量.
1 力与向量
向量的英文是,中国的物理学家们在清末民初时期引进西方科学概念时将“”称为“矢量”,至今向量与矢量两种译名共存,究其原因,早期的向量只是物理学专门用来表示力和速度等“既有大小又有方向”的物理量的工具,并不为数学家们所重视,因此“矢量”的译名一度流行.
实际上,力作为向量最常见的实例有着十分古老的渊源.大约在公元前350年,古希腊著名学者亚里士多德就知道了力可以表示成向量,两个力的合力可用平行四边形法则得到,随后古希腊数学家海伦则给出了该法则的几何证明.
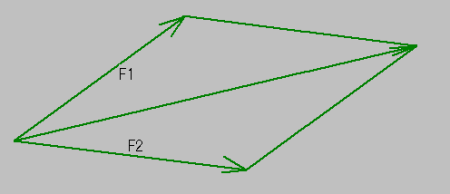
力的合成
在现实生活中,处处有“力的平行四边形法则”,比如中国古代的“驷马车”,可以直观地依据平行四边形法则观察到这样的合力.
古希腊之后的1500多年,经过了漫长又黑暗的中世纪,向量的知识都没有什么太大的变化.牛顿在其著作《自然哲学的数学原理》中总结了前人的智慧,论述了力、速度等物理量作为矢量如何进行运算,其本质还是向量的平行四边形法则.可见,这点向量知识,形不成多少有意义的数学问题,不能发展成一个独立的学科,因此数学家们并没有重点将向量作为对象进行深入地研究.
2 复数与向量
直到19世纪,事情开始发生变化,“复数”在向量的发展中充当了催化剂.
数学家韦塞尔和阿尔冈发现了复数的几何表示,这是一个具有划时代意义的数学发现,随后德国数学家高斯建立了复平面的概念,从而使得平面向量与复数一一对应起来.向量可以表示为一组有序实数对,这与复平面中的复数是一致的.
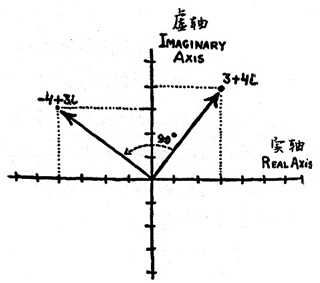
复数——数的最后乐章
当时的数学家们想到,复数可以看作“二维向量”,那么单个实数就可以看作“一维向量”,同理,一定也还有“三维向量”、“四维向量”,乃至“维向量”.
于是,爱尔兰数学家哈密顿首先研究了“四元数”:
这种具有4个分量的数具有诸多神奇的性质,它构成的数系能够进行加减乘除四则运算,但是美中不足的是要放弃乘法交换律.
尽管如此,这一伟大的发现引起了又一位大牛的注意,代表着19世纪物理学重要发展方向的著名物理学家麦克斯韦对四元数情有独钟,他对于四元数在电磁学中的应用使人们逐步认识到用向量处理物理问题的必要性.
麦克斯韦在其著作《电磁通论》的绪论中写道:
“
对于物理推理的许多目的来说,不同于计算,有必要避免明确地引入笛卡尔坐标,并把注意力固定在一个空间点上而不是在它的3个坐标上,固定在一个力的大小和方向上而不是它的3个分量上.这种考虑几何量和物理量的模式比另一种模式更原始、更自然,尽管与它相联系的那些概念直到哈密顿通过发明他的四元数演算而在处理空间问题上迈出一大步才得到充分的发展.……然而,我确信,四元数的概念而不是四元数的运算和方法的引入,对我们的课题的所有部分的研究将是大有用处的;特别是在电动力学中,在那里我们必须讨论许多物理量,而他们彼此之间的关系可以用哈密顿的少数几个表达式来表示,比用普通的方程要简单得多.
可见,随着复数与向量理论的深入,物理学科的相关知识(尤其是电学)也得到了发展.
3 “四维向量”与中国古诗文化
提到四维向量,现在让我们一起来欣赏初唐诗人陈子昂的著名诗篇《登幽州台歌》,体会其中蕴含的数学文化意境:
“
前不见古人,后不见来者.念天地之悠悠,独怆然而涕下!
这便是古人对时间与空间看法的文学表述.陈子昂的时空观,就是欧几里得的时空观,也是今天人们普遍持有的朴素时空观.
从数学上看,这是一首阐发时间与空间感知的绝妙佳作.前两句表示时间可以看成一条直线(一维),以诗人自己为原点,前不见古人指时间可以延申至负无穷大,后不见来者则意味着未来的时间是正无穷大,后两句则指向了“天和地”构成的三维现实空间.因此,如果此时此刻为,我们在三维空间中的位置为,那么每个人在“四维空间”中都对应了一个独特的向量:
陈子昂在诗中感叹天地之宏大,时间之遥远,不禁觉人生之短暂,遂产生敬畏之心,这样的意境,对于数学家和文学家来说是可以相通的.
4 维向量
沿着四维向量往前走,维向量逐渐被拨开迷雾展现在人们面前.
德国数学家格拉斯曼于1844年引入了维向量的概念.仿效平面向量的记法,我们将一个维向量定义为一个维的数组:
维向量可以定义加法和减法,也可以用单个实数与其相乘.向量的数量积也可以推广到维情形.这就是向量空间(线性空间)要研究的问题.
实际上,维向量看似很“高端”,但是它在生活中其实有着非常直观的意义,比如说我们去商场购物,种商品的“单价向量”
以及种商品的“数量向量”
那么两者的数量积,实际上就是你的总付款金额
因此,所谓的维向量的数量积,其实就在我们身边.
时至今日,“个”成为当今社会的流行语,用来表示“很多个”的意思,比如“我有个选择”,“这件事有个因素”等等,究其根源,正是维向量等数学名词广泛普及的结果.
审核编辑:刘清
- 相关推荐
- 热点推荐
- 向量
-
24位或者说高分辨率的AD到底有什么用呢?2025-01-07 427
-
反码位是什么?到底有什么用?2021-05-07 2154
-
64-Kbit FRAM是什么?64-Kbit FRAM到底有什么用途?2021-06-17 1619
-
模拟看门狗到底有什么用处呢2022-01-17 1437
-
异常处理向量表的设置中DCD这些伪指令到底有什么用?2023-02-28 1393
-
数据可视化到底有什么用?2018-02-05 26697
-
工业互联网, 你到底有啥用?2020-03-01 4044
全部0条评论

快来发表一下你的评论吧 !

