量子霍尔效应详解

我们学习固体物理，特别是学习量子凝聚态时，学得越久，对其中一系列现象的认识就越深入、对其深邃广博的体会就越深刻。其中，有两类物理效应最让人惊奇而着迷。一是超导电性：虽然芸芸百姓对超导能不能普遍应用还感受不深，但被超导电性关联起来的物理却已经覆盖物质科学的诸多分支。一是量子霍尔效应 (quantum Hall effect, QHE)：自半导体异质结二维电子气中发现量子霍尔效应 (quantum Hall effect, QHE) 开始，到今天将拓扑绝缘体与 QHE 紧密联系起来，量子霍尔效应同样覆盖了量子凝聚态前沿的诸多分支。因此，触及这两类效应之一，就是令人唧唧称道的生活了，更别说两者均沾会更加了不起。

以 QHE 为例，外加磁场加持朗道能级填充，在异质结界面处形成的二维电子气中会表现出量子化的输运，表象则是边缘态展现的霍尔电导整数台阶化，如图 1 (上部) 所示。在高磁场下，还可能出现分数化霍尔电导台阶。这些台阶化行为，背后的物理，是无数电子个体恰到好处地协调统一起来。它们步履一致、集体行动，形成宏观的量子化，令人击赏！

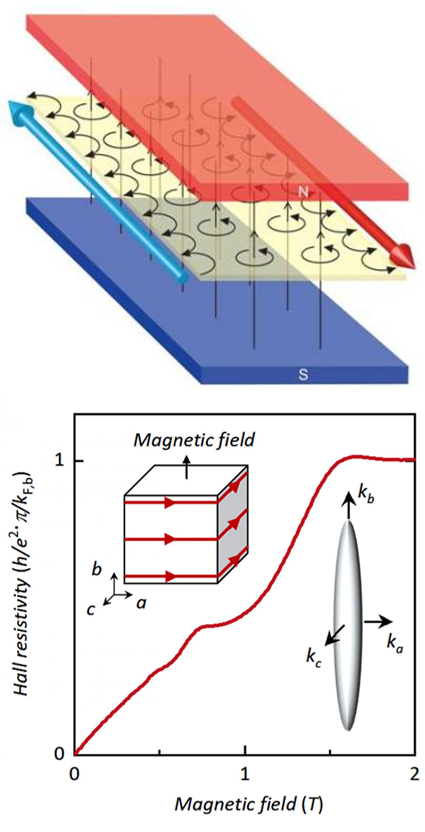
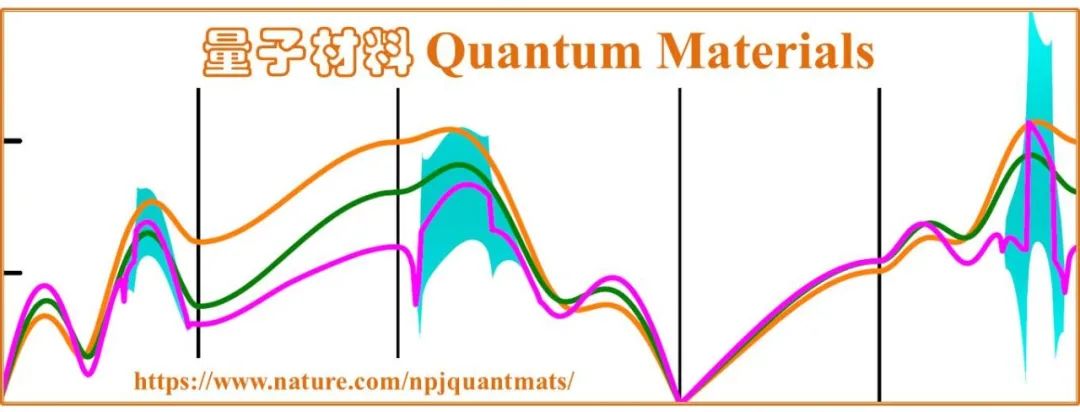
图 1. 量子霍尔效应 QHE 的物理图示 (上图) 和 ZrTe5 中观测到的类 QHE (三维体系的柱状费米面形态很特别、各向异性很强)。

其实一直到不久前，所有关于 QHE 的实验观测，基本上都与二维体系的量子传输效应密切相关。这似乎给了我们一个思维定式：QHE，总归是二维体系中朗道能级填充导致的边缘态的表现。即便是众所周知的三维体系，如拓扑绝缘体，虽然体系是三维，但实际的物理依然是二维的。也就是说，拓扑非平庸性质约束能带结构，在体系表面处形成新物理，磁场作用下体系形成独特的表面和边缘态，贡献了 QHE。因此，这里的三维体系展示的 QHE 更强化了我们对 QHE “只存在于二维”的思维定式。

当我们愈加渲染这种二维物理的魅力时，物理人天生的“猎奇”和“反骨”脾气就愈加显现。我们的问题是：真实的三维体系中，有没有这样的 QHE？哪怕是形似而神不似的类 QHE，也是令人遐想的。实际上，这样的行踪最近有迹可循。大约是 2019 年前后，就有一些前沿报道，包括中国学者的工作，揭示出 ZrTe5 这类体系中就存在三维 QHE 效应。图 1 (下部) 显示的即是一个结果，其中插图展示了高度各向异性的费米面特征 (柱状 cylinder 费米面)。

不过，如果这样的 QHE 能在更多三维体系中被观测到，特别是在与超导电性有关的体系中被观测到，一定更很有意思。众所周知，高温超导电性，无论是铜基还是铁基，其相图展示的物理有一定程度的相似性。它们都是从反铁磁母体基态出发，通过适度的载流子掺杂，诱发出赝能隙相区 (铜基) 或自旋密度波 SDW区域 (铁基)，如图 2 所示 (上部是铜基、下部乃铁基的典型相图模样)。

对铜基超导体，在赝能隙相区，有电子库珀对形成，似乎是超导态前期的萌生态。当这些库珀对浓度足够高、并能够如宏观 BEC 一般凝聚时，就形成了 well – defined 的超导能隙和超导电性。这样的物理，对量子材料人而言已驾轻就熟。也因此，我们就很关注这一超导母体的反铁磁基态区有哪些有趣的物理？能不能对超导电性有推动作用？这样的单纯动机，应该是我们开始行动的无上驱动力，虽然此时未必想到其中还有 QHE。

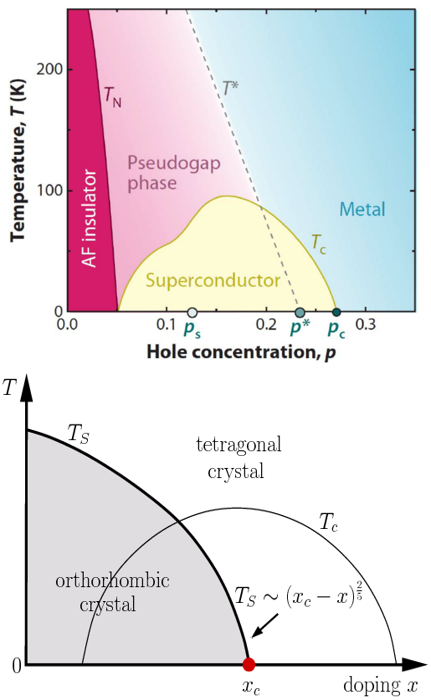
图 2. 铜基 (上部) 和铁基 (下部) 超导相图的大概模样。虽然它们很多不同，但母体反铁磁基态是类似的。

于是乎，就有若干量子材料人开始关注铁基超导母体中的反铁磁态及其电子结构。令人有些吃惊的是，有研究揭示出，在诸多铁基超导体系的费米面附近，能带结构具有非平庸拓扑特征。这一结果如今不算什么大事情，因为物理人通过地毯式搜索，已经揭示出现在的物质世界有很高比例都是拓扑非平庸的拓扑量子物质。如此，在超导电性体系中找到拓扑量子性质，除了增加拓扑物理的魅力、增加超导电性的魅力之外，其实也并无特别令人诧异之处。

好吧，我们继续。有一些深入的分析结果似乎揭示出，在铁基超导体的反铁磁母相中，自旋波的能隙并未完全打开，而是在费米面处形成了一个或多个能隙节点 (node)。这一独特结构，催生了 node 处狄拉克费米子，展示出类似二维半金属之类的特征。在输运行为上，这可能对应于反铁磁半金属特性。具备如此性质的一个体系，就是著名的 1111 铁基超导母体 LaFeAsO 之变体 CaFeAsF。

来自日本 NIMS 的 Taichi Terashima 博士，是日本在铁基超导和拓扑物理领域的一位活跃学者。他主持的团队一直致力于 CaFeAsF 的相关研究。他们前期揭示出 CaFeAsF 费米面独特的形貌特征，即在节点 (node) 处存在一对由对称性保护的 α - 狄拉克电子柱(a pair of α - Dirac electron cylinders)，在布里渊区中心处也存在一 β - 薛定谔空穴柱(β - Schrödinger hole cylinder)，如图 3 所示。这一高度各向异性的费米面形态，才使得体系载流子输运呈现类二维特征。

图 3. CaFeAsF 的布里渊区中费米面的形貌特征，展现了 α - 狄拉克电子柱对和 β - 薛定谔空穴柱。这一特征与图 1 中 ZrTe5 的能带 (下部的柱体费米面示意图) 有些相似性、但更丰富。

更多的联想，自然还是要基于实验观测：(1) 对 CaFeAsF，沿其 c 轴和 ab 面测得的电阻率相差 200 倍以上，的确有很强的二维输运特征。这表明，外加磁场作用下出现 QHE 的必要条件已初步具备。(2) 测量得到的 CaFeAsF 载流子浓度，与典型的二维狄拉克半金属 EuMnBi2 和重掺杂拓扑绝缘体 Bi2Se3 等载流子浓度水平相当，而后两者都呈现出量子霍尔效应 QHE。这意味着，CaFeAsF 出现 QHE 的另外一个条件也基本具备。就是说，在 1111 型铁基超导母体 CaFeAsF 中，很可能存在只有那些二维体系中才能经常看到的 QHE，虽然从晶体结构上看 CaFeAsF 的确是一个三维体系。

上面的这些肤浅、粗糙之评论，自然都是小编在阅读一篇论文后的马后炮。这篇论文，乃出自 Terashima 博士与中科院上海微系统研究所牟刚博士他们之手，刊登于最近的《npj QM》上。论文作者包括来自佛罗里达州立大学强磁场实验室和京都大学的物理人。

在这篇文章中，他们通过系统实验和数据解构，特别是高磁场下的磁输运测量，包括纵向电阻和霍尔电阻同步测量，然后通过张量变换得到纵向电导和霍尔电导数据，如图 4 所示。实验结构展示出，CaFeAsF 在接近 40 T 强磁场、0.4 K 温度下，存在一个朗道能级填充因子 ν = 0 的 QHE。更进一步，他们想表明，这个 ν = 0 的 QHE，并非是那种直接观测到的 QHE 量子化台阶，而是高磁场下电子填充 ν = 2 之量子霍尔效应和空穴填充 ν = 2 之量子霍尔效应的叠加组合，从而得到 ν = 2 (电子) – 2 (空穴) = 0 这一复合效应，很是令人惊奇！

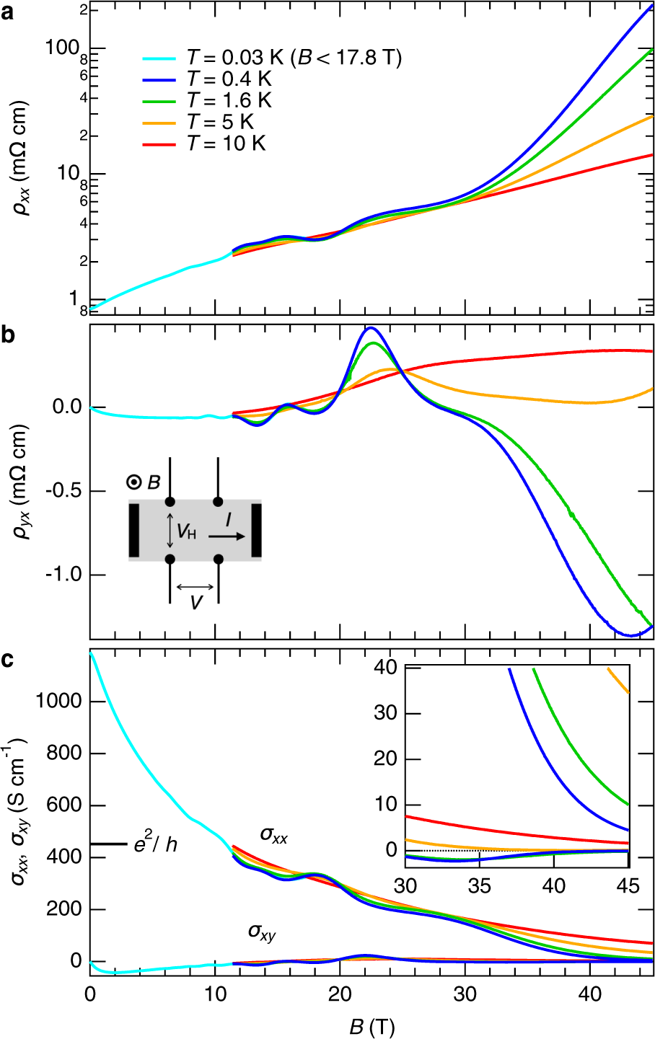
图 4. 对 CaFeAsF 单晶测得的面内磁传输数据，磁场 B 沿 c 轴方向。

总结学习体会，小编以为这一工作的新颖之处无非是：三维铁基超导母体中存在 QHE 的一些特征，只是这一特征是布里渊区电子和空穴各自构成的费米面柱的组合表现，也就是 ν = 0 的量子霍尔效应。这是第一次在铁基超导母体中呈现此类效应，从这个意义上看，此工作也算有一些不平常之处。谁知道呢？量子霍尔效应与超导电性“复合”，至少可以让我们梦想一下诸如拓扑超导、量子计算之类的前景。不过，三维块体倒是三维块体，这里目前还只能得到 ν = 0 的量子霍尔效应，它是一个复合态吗？能不能进行直观区分、表征和各自调控？使得针对电子和空穴的纯净 QHE 能显现出来。这些都是较为重要的问题，富于挑战。

审核编辑：汤梓红