最大限度地保持社交距离是 COVID-19 的后果

专家、医生和科学家表示，为了限制冠状病毒感染，人们在社交接触中应保持至少 1 米的人际社交距离。但是，独自呆在家里，被感染的风险为零。本文不打算谈论有关冠状病毒的医学或科学新闻。它将提出一种替代算法，用于在明确定义的区域内进行人员分布，以使他们尽可能远离。显然，所提出的方法不是解决问题的最佳解决方案之一；它基于蒙特卡洛系统。该系统提供了一种最简单的人员分配方式。

目标
该程序的最终目标是将一定数量的人放置在特定的空间中，使他们之间的距离足够远，以避免病毒传播的风险。可用空间由一个网格或 N × M 方阵表示。人由同一网格上的标记表示。为了实现这一目标，有许多方法和许多数学和 IT 程序。无论如何，它是一个旨在最大化人与人之间距离的系统。该问题可以通过使用线性规划系统、非线性规划系统、递归算法或使用蒙特卡罗研究来解决。显然，后者不能确保出色的结果，但对于大多数应用程序来说，它是更复杂和要求更高的程序的有效替代方案。

蒙特卡洛方法
蒙特卡洛方法是一种基于随机抽样获得数值结果的计算方法。它用于通过模拟获得估计。它基于一种算法，该算法生成一系列彼此不相关的随机数，这些随机数遵循这种现象的可能分布。

网格
为了表示空间上的人，我们可以使用由许多单元格组成的 2D 网格 (N × M)。我们可以将网格或矩阵想象成一个棋盘，上面放置了一些人或物体（图 1）。网格按行和列组织，因此任何编程语言都可以轻松管理它。组织、填充、滚动和查询矩阵相对容易。为了获得这些结果，我们可以使用两个嵌套的迭代循环和一些“if”条件。网格（方阵）代表人们可以在上面的有用空间。每个单位对应1米；因此，每边10个方格组成的网格相当于100平方米的面积。该算法考虑了一个人和另一个人之间的倾斜距离。在横向位置的情况下，将使用勾股定理计算距离。

图 1：网格类似于棋盘，棋子必须放在尽可能远的位置。

我们可以使用什么编程语言？
这是计算机程序员最关键的问题之一。有数百种编程语言，每种都有其优点和缺点。我们算法面临的问题与研究有关。这是一个涉及数十亿次迭代的蛮力程序。很明显，为了我们的目的，必须使用一种速度极快的编程语言。可以使用更简单、更图形化的语言更好地以图形格式表示最终信息，但我们决定考虑速度和性能方面，以涵盖执行期间的最高计算次数。此外，为了提供通用代码，我们更喜欢使用适用于任何环境和任何操作系统的 C 语言。

算法
该过程的算法非常简单（图 2）。令人惊讶的不是真正的方法，而是代码执行的大量工作。实际上，在无限循环中，地图不断被破坏和重建以寻找最佳解决方案。C 语言的速度有助于实现更实用、更强大的搜索。代码执行以下阶段：变量和函数的准备以及主函数的执行。在其中，循环执行以下任务：重置网格，在网格上随机放置人口，以及确定（打印）最佳距离。所有这些工作都以非常高的速度进行。

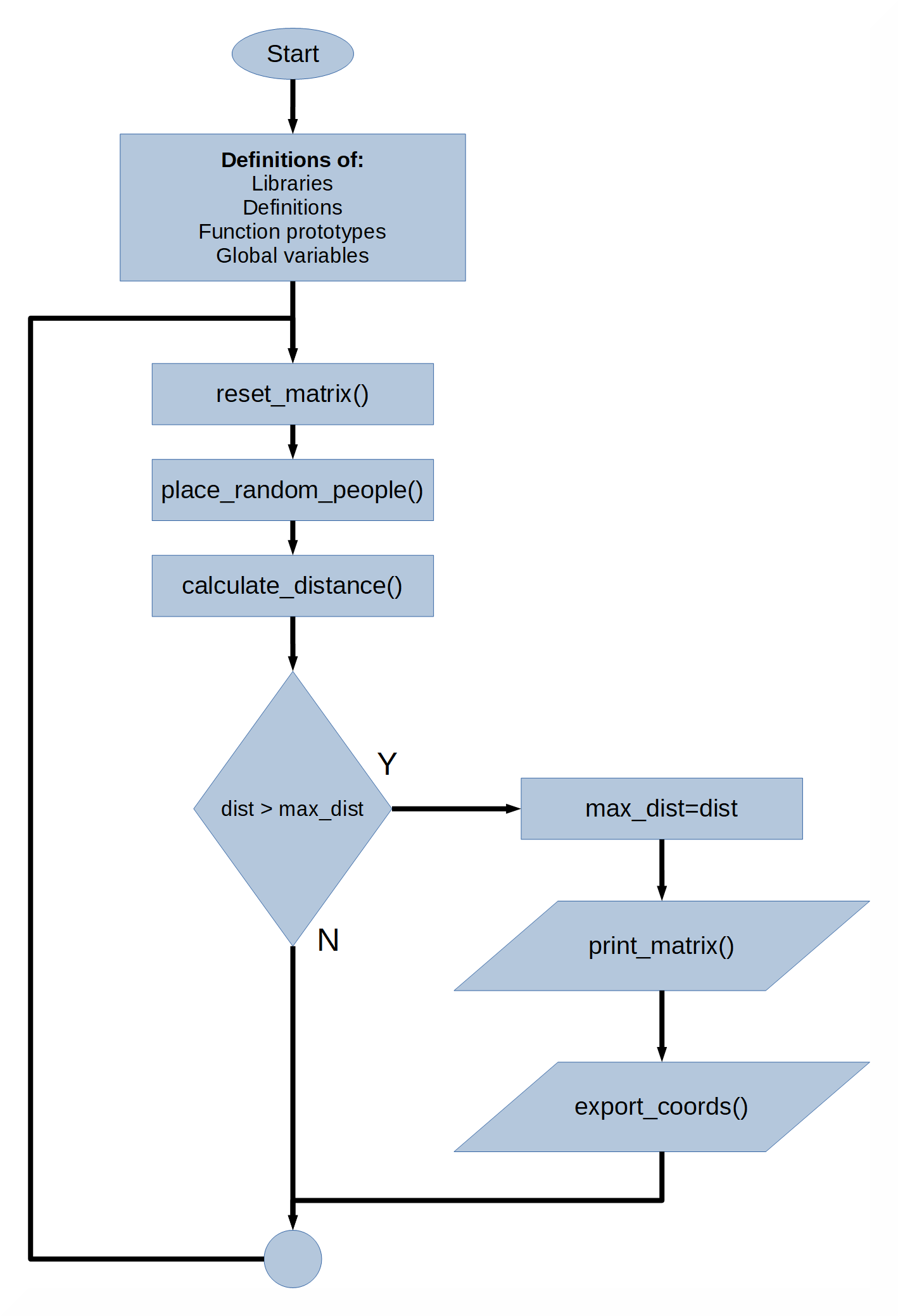
图 2：程序流程图

软件
您将找到本文所附的程序源代码 (.C)。它分为几个逻辑部分。它从包含文件开始，其中加载了软件中使用的函数的原型，例如在数学库中。然后我们可以找到列数、行数、人数等全局值的定义。这些值在整个程序中是全局可见的。用户可以自由修改这三个值（图 3），但重要的是要记住，如果值太高，搜索时间会受到影响。

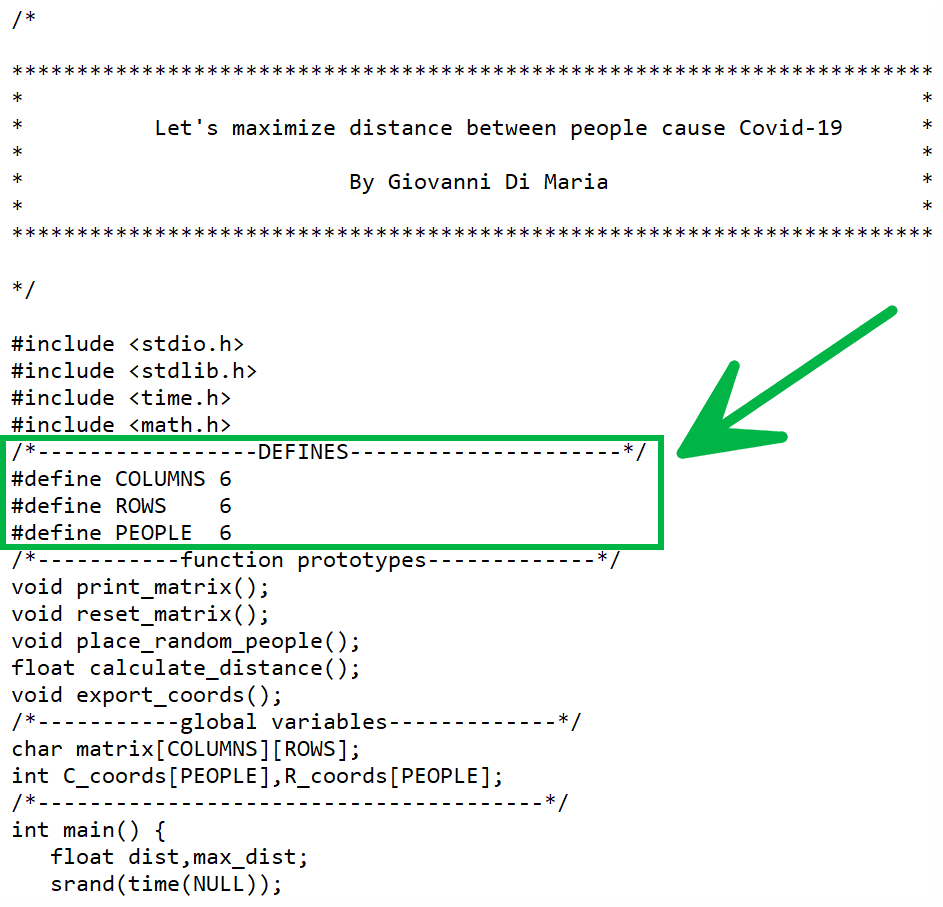
图 3：您可以修改三个定义来改变研究领域。

程序的下一部分包含函数的原型。然后我们可以看到全局变量的定义。最后，“main()”函数开始。它包含一个非常短的无限循环，其中重复以下功能：

电网重置；

人口的随机分布；

计算最佳距离；

确定最佳结果的可视化；

将结果导出到 Octave。

这些任务被循环和无限期地执行，因为它们包含在“while”循环中。源代码中使用了以下 UDF 函数：

第一个函数是“print_matrix()”。它在屏幕上显示矩阵。

下一个 UDF 函数是“reset_matrix()”。它使用双嵌套循环将存储“-”字符的网格归零。

下一个函数是“place_random_people()”。它将人置于矩阵内。条件控制确保良好的定位并在单元格已被人占用时丢弃随机数，重复提取。

下一个 UDF 浮点函数是“calculate_distance()”。它计算两点之间的距离。它计算并返回人与人之间的最小距离。注意，如果点是倾斜排列的，软件使用勾股定理来计算相对距离。

下一个函数“export_coords()”将数据导出到 Octave 数学环境，以优雅地显示结果。

添加特定功能后，软件总是会生成不同的随机序列。事实上，在清单的开头插入以下语句就足够了：

srand (时间 (NULL));

通过消除这条指令，生成的数字的顺序总是相同的，这对调试程序很有用。目前，该程序会找到人与人之间的最小距离，因此会最大化这个数字。要在代码中实现的其他标准可以如下：

最小距离的最大化

平均距离最大化

不同区域的距离最大化

编译
编译源代码很容易。您无需修改代码即可将源代码与其他编译器一起使用。如下图，根据使用的编译器，可以找到一些编译的例子。一些解决方案为速度优化提供支持：

海合会

gcc distance.c -Wall -O3

TCC

tcc 距离.c

橙色 C/C++ 编译器

occ 距离.c

实验
我们已准备好尝试该程序。第一个要进行的测试涉及小范围内的几个人。要设置的值是：

/*——————定义——————*/

#define 列 6

#define 行 6

#定义人 6

使用命令“distance.exe”启动程序执行后，我们将在监视器上看到第一个结果，显示网格上人员的最佳配置（图 4）。如果计算机找到更好的结果，这些结果将显示在屏幕上并作为新的解决方案呈现。这些解决方案寻找人与人之间的最大距离。

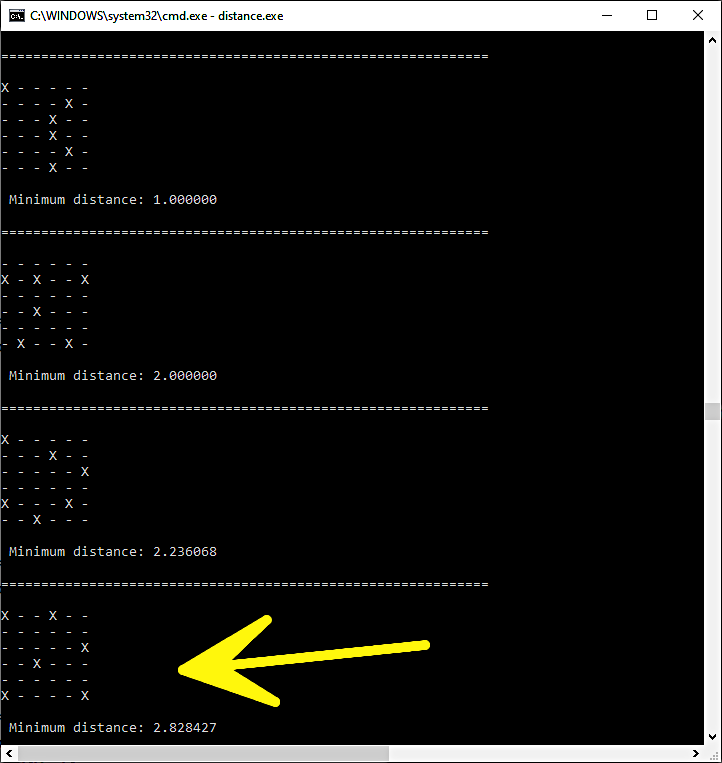
图 4：6 人的 6 × 6 网格的解决方案

更强大的实验可以在更大的区域内使用更多的人进行。下一个实验应具有以下值：

/*——————定义——————*/

#define 列 20

#define 行 10

#定义人 16

在这种情况下，处理步骤更重。解决方案的显示速度要慢得多，而且不是最好的。图 5显示了一种可能的解决方案，但不是最佳解决方案。

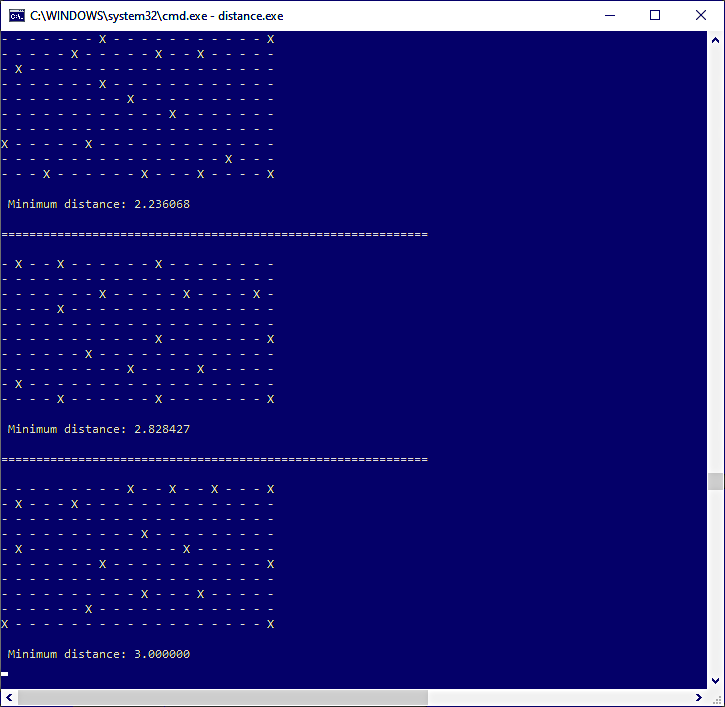
图 5：16 人的 20 × 10 网格的解决方案

变化
两个人之间的距离可以用不同的方式和许多标准来衡量（图 6）。一种方法是将距离计算为理论矩形三角形的斜边，如果人们倾斜排列的话。这种计算是最真实的，因为它通常以这种方式发生。

d = sqrt([cat1 × cat1] + [cat2 × cat2]);

另一种方法将距离视为两个人之间的平方数。在这种情况下，人的位置是直角还是斜角都没有区别。

d = abs(cat1) + abs(cat2);

程序员可以选择计算距离的首选方法。

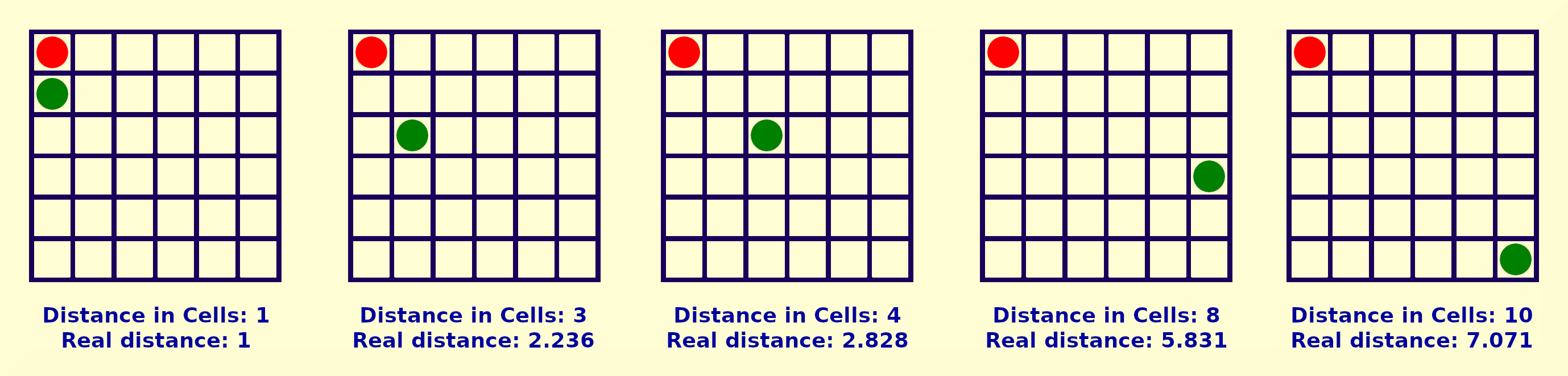
图 6：测量两点之间距离的不同标准

图形结果
C语言程序直接在视频上显示人的位置地图。这种可视化是在终端上进行的；因此，图形方面不是非常令人愉快。然而，该程序提供了一个数据导出功能，允许将信息和点的坐标导出到文本文件，并允许作为脚本直接导入 Octave 数学环境。这样，从图形的角度来看，地图与人的可视化更加令人愉快和有吸引力。正是当程序找到一个新的解决方案时，除了在监视器上显示结果之外，它还将它们作为 Octave 的脚本保存到一个文本文件 (distance.m) 中，其中包含绘制图形地图的有用信息（图 7）。这样，显示的地图将与文本地图相同，但具有更加美观和优雅的图形外观。

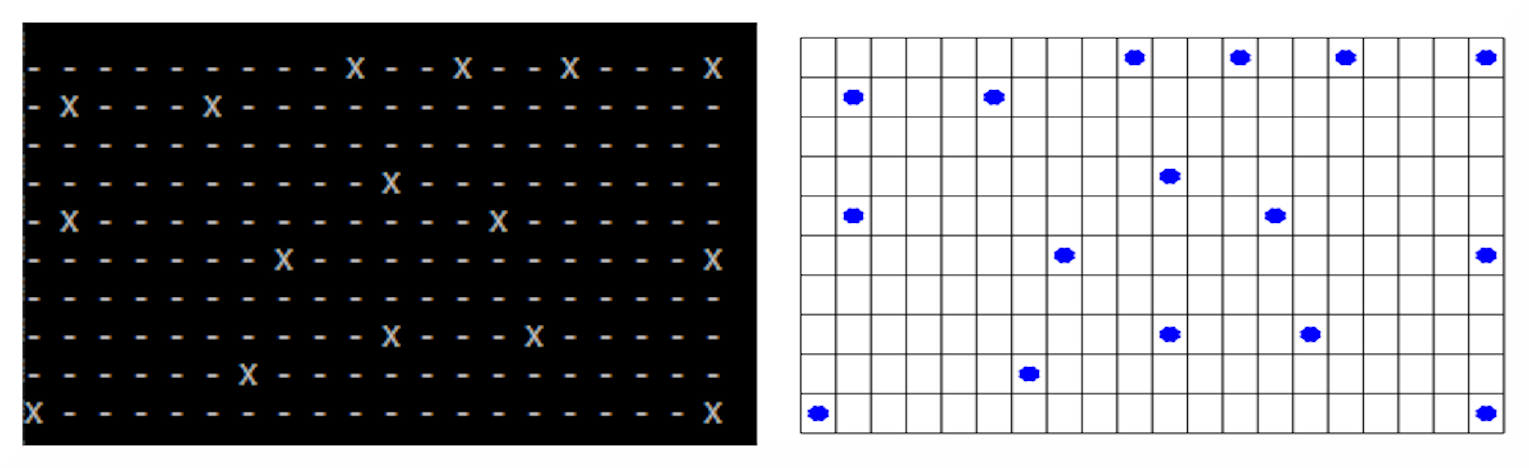
图 7：文字地图和图形地图是等价的。

下面，我们可以看到一个 Octave 脚本的示例：

坚持，稍等;

情节（19、9、'b*'、'线宽'、11）；

情节（15、9、'b*'、'线宽'、11）；

情节（12、9、'b*'、'线宽'、11）；

情节（ 9 ， 9 ， 'b*' ， '线宽' ， 11）；

线（[-0.5,19.500000]，[-0.500000，-0.500000]，'颜色'，'k'）；

线（[-0.5,19.500000]，[0.500000,0.500000]，'颜色'，'k'）；

线（[-0.5,19.500000]，[1.500000,1.500000]，'颜色'，'k'）；

线（[-0.5,19.500000]，[2.500000,2.500000]，'颜色'，'k'）；

线（[18.500000,18.500000]，[-0.5,9.500000]，'颜色'，'k'）；

线（[19.500000,19.500000]，[-0.5,9.500000]，'颜色'，'k'）；

暂缓；

非常大的数字！

人在网格上的定位相当于组合计算的“简单组合”的计算。简单组合的数量如图 8所示。以下是一些显着结果的例子：

6行×6列×6人：1,947,792种组合

20行×10列×16人：169,152,626,591,028,520,278,300种组合

50行×20列×40人：555,974,423,571,664,033,815,804,589,243,553,849,851,258,056,649,719,919,687,842,027,223,208,475种组合

我们可以立即理解，对于这些非常高的数字，蛮力方法是无法解决的。

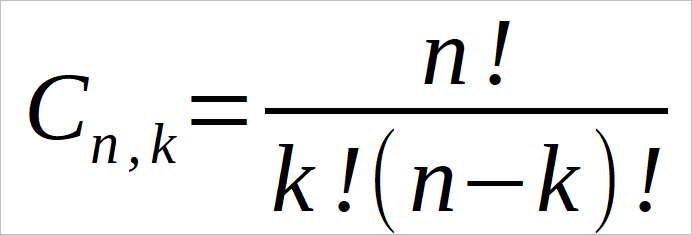
图 8：简单组合的公式

结论
本文介绍的研究方法不是最好的，也无法找到最好的结果。获得的组合可用于对本文主题中提出的问题进行一般估计。蒙特卡洛方法有很多限制，例如它的相对缓慢。否则不可能，因为程序可以生成的数据和信息数量非常多（数十亿个组合），没有计算机或人类能够计算出这样的数字。对于相对较少的信息，达到最终解决方案很简单。但是如果对象的数量或网格的尺寸增加，计算时间将成倍增长。增加搜索参数很不方便。该程序采用的方法也被定义为“蛮力”。计算上，这是一项非常繁重的工作，不能确定最终结果，并且可能会多次重复相同的解决方案。但是这种方法对于所有那些运行参数和因变量非常多的研究应用来说确实很有用。有时，寻找可能的解决方案可能会持续一整夜，尤其是在网格非常大且人数众多的情况下。搜索时间还取决于计算机的速度和使用的编译器类型。本文中进行的实验可以为程序员创建更复杂和更复杂的程序提供新的思路。它代表了未来功能发展的起点。该程序的一个有趣的实现也可以包含人工智能。为这个非常复杂的目的确定最终解决方案可能很有用。本文所附的操作代码是用 C 语言编写的，可以很容易地翻译成任何其他编程语言。程序注释足够，任何程序员也可以找到其他点来修改和改进它。除了提供教学实用程序之外，本文中采用的过程在代码编写和使用方面都非常有趣。该系统是完全自主的，因为程序提供的结果是不可预测的，因为数据和信息是随机处理的。任何程序员也可以找到其他点来修改和改进它。除了提供教学实用程序之外，本文中采用的过程在代码编写和使用方面都非常有趣。该系统是完全自主的，因为程序提供的结果是不可预测的，因为数据和信息是随机处理的。任何程序员也可以找到其他点来修改和改进它。除了提供教学实用程序之外，本文中采用的过程在代码编写和使用方面都非常有趣。该系统是完全自主的，因为程序提供的结果是不可预测的，因为数据和信息是随机处理的。

审核编辑 黄昊宇