探索NX CAE工程仿真——从弹簧系统构建说起

导读：CAE初学者往往花大量精力在3D和2D网格划分的练习上，却不愿花时间在1D和0D单元建模的专题学习和强化训练上，造成了在工程中一旦遇到存在弹簧、质量、阻尼器和缓冲器等单元类型的构件和结构时，往往感到措手无策和无从入手，其根本原因在于忽略了CAE学习中的基础单元创建和结构简化建模思路学习的重要性。

下面从一个弹簧建模开始，结合理论计算进行相应的方案仿真和分析，由简到繁逐步过渡到单自由度质量-弹簧-阻尼系统的构建和谐响应响应分析，为后续多自由度质量-弹簧-阻尼建模以及进行更加复杂的瞬态、频率和随机振动等动力学响应分析理清思路和夯实基础。

一、创建弹簧模型及其分析

1、建立弹簧模型和计算要求

一个刚度为10N/mm的一维拉伸弹簧，一端固定，一端承受外力为1Kg，根据理论公式计算其位移最大的变形量为1mm，本文需要对该弹簧进行建模并仿真求解。

2、弹簧模型的构建方法

NX CAE/Simcenter 3D提供了3种构建弹簧模型的方法，方法1首先在建模环境中构建一条直线（本文中定义长度为200mm，方向为ACS/WCS的Z向），在Fem对话框中需要打开并勾选几何体选项中的【直线】选项，进一步进入Fem环境中划分1D网格并依次定义弹簧的刚度参数和方向；方法2直接进入Fem环境构建直线并划分1D网格并依次定义弹簧的刚度大小和方向；方法3（本文采取的操作方法）在建模环境新建主模型（命名为K01）并进入Fem环境中，利用【节点创建】命令中的指定点坐标值功能，依次创建出2个节点，然后利用【单元创建】命令，依次选择单元族类型为【1D】、单元类型为【CELAS1】（或者CELAS2），单击选中上述创建好的2个节点，即可创建出弹簧单元（通过编辑显示，加粗符号、改变颜色和增加文本SP）和在仿真导航器窗口增加了相应的特征树节点1D收集器Celas1 Collector（1）1d_manual_mesh（1），如图1所示。

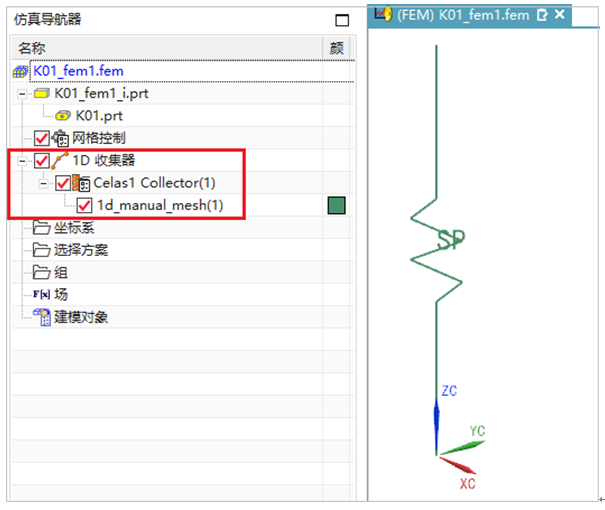
图1 构建的弹簧模型

按照上述弹簧建模方法，可以进一步构建出两个弹簧“串联”和“并联”的模型。

3、定义弹簧模型的参数

单击仿真导航器窗口中的特征树节点【1d_manual_mesh（1）】，通过【网格相关数据】定义该弹簧的A/B端分量均为Z，如图2所示。点击【Celas1 Collector（1）】，编辑并弹出【网格收集器】对话框并点击【编辑】，弹出如图3所示【PELAS】对话框，默认物理属性名称，在属性【平移刚度】中输入10（单位为默认的N/mm），其中属性中【阻尼系数】是指该弹簧的迟滞（结构）阻尼值（物理阻尼），此处不必定义，这样完成了设置弹簧刚度大小的操作。

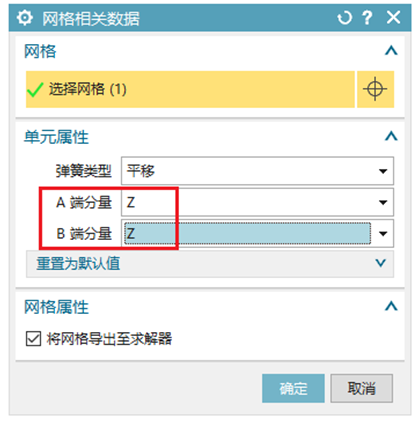
图2 定义弹簧的方向

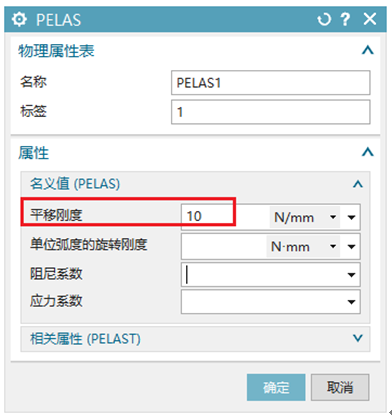
图3 定义弹簧刚度大小

4、建立仿真模型并求解

新建仿真并进入Sim（仿真）环境，求解器为默认的【Simcenter Nastran】、解算类型为默认的【SOL101 线性静态-全局约束】，利用约束类型中的【固定约束】对弹簧的上端节点进行固定，选中载荷类型中的【力】并在其对话框中输入10N、指定受力方向（-Z），求解后进入后处理界面，加载并打开结果文件中的【位移-节点/Z】，即可得到如图4所示的弹簧位移云图，显然解算得到的最大值和理论计算值一致，即为1mm。

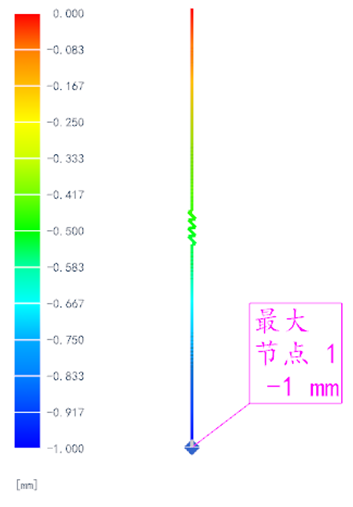
图4 弹簧位移的解算结果

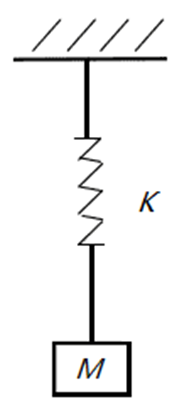
图5 弹簧-质量模型示意图

二、创建弹簧-质量模型及其分析

1、弹簧-质量模型及其计算要求

如图5所示为一个单自由系统弹簧-质量模型的示意图，上端固定，设定弹簧刚度k为10N/mm，质量M为1Kg，借助理论力学中关于无阻尼单自由度弹簧-质量系统固有频率的计算公式，可以计算其固有角频率（圆频率）ω0为100Hz，固有频率f为15.924Hz（具体的计算过程不再赘述）。本文需要对该弹簧-质量模型进行建模并仿真求解其固有频率。

2、弹簧-质量模型的构建方法

在掌握上述弹簧模型构建方法基础上，在建模环境中新建一个弹簧-质量的主模型（命名为KM_01），并在Fem环境中按照上述操作构建好弹簧模型（符号为SP），再次利用【单元创建】命令，依次选择单元族类型为【0D】、单元类型为【CONM1】（或者CONM2）、单击上述构建好的2个节点，即可创建出0D质量单元，这样在仿真导航器窗口增加了相应的特征树节点0D收集器Concentrated Mass Collector（1）d_manual_mesh（1），通过编辑显示修改颜色并切换标记类型为【填充大正方形】，勾选文本符号（CM）的显示，如图6所示。

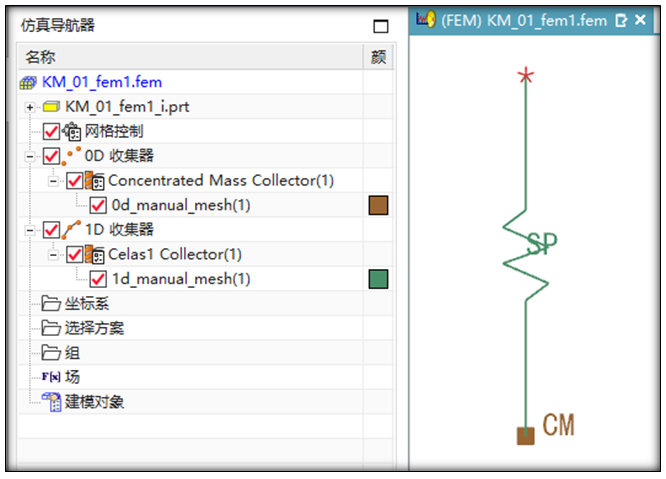
图6 创建弹簧-质量模型及其特征树节点

3、弹簧-质量模型参数的定义

单击仿真导航器窗口中的【0d_manual_mesh（1）】，右键并通过【网格相关数据】定义该单元属性的质量值（［质量33］代表了Z方向）为1Kg，即可完成了定义质量属性的操作。

4、建立仿真模型并求解

新建仿真并进入Sim环境，求解器为默认的【Simcenter Nastran】但将解算类型切换为【SOL103实特征值】，利用约束类型中的【固定约束】对弹簧-质量模型的上端节点进行固定，求解后进入后处理操作界面，加载并打开结果文件Structrual，可以看到【模态1】（单自由度模型只能有1阶振型和1个固有频率值）的大小为15.9155Hz，和理论值15.924Hz非常接近。

三、创建单自由度质量-弹簧-阻尼模型及其分析

1、单自由度质量-弹簧-阻尼模型及其要求

如图7所示为一个单自由系统质量-弹簧-阻尼模型的示意图，上端固定，设定弹簧刚度k为10N/mm，质量M为1Kg，阻尼系数C为63N.S/m（理论阻尼比ξ换算为0.315，无量纲），激励力F=F0*sin（ω*t），其中F0的幅值为2000N，ω为激励角频率，t为0～1s。

通过理论公式可以求解该系统的固有角频率ω0为100Hz，现采用NX前/后处理进行建模并仿真求解其固有频率、阻尼频率以及当ω=ω0时系统谐响应位移X（t）的变化规律。

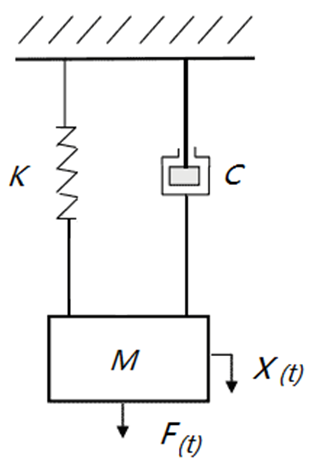
图7 质量-弹簧-阻尼模型示意图

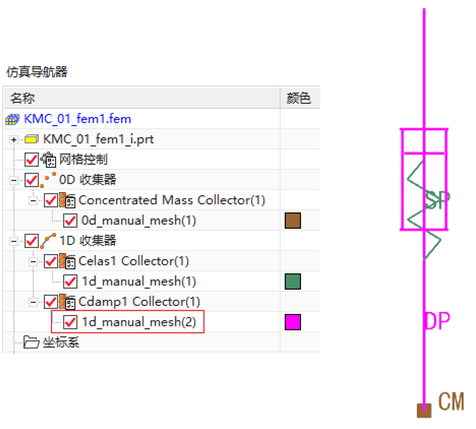
图8 质量-弹簧-阻尼仿真模型

2、质量-弹簧-阻尼模型的构建方法

在掌握上述弹簧-质量模型构建方法基础上（同时定义好各自的属性参数），在建模环境中新建一个质量-弹簧-阻尼的主模型（命名为KMC_01），并在Fem环境中按照上述操作构建好如图6所示的弹簧-弹簧模型，再次利用【单元创建】命令，依次选择单元族类型为【1D】、单元类型为【CDAMP1】（也可以选用CDAMP2、CVISC、CBUSH1D等阻尼形状的单元）、单击上述构建好的2个节点，即可创建出阻尼单元，同时在仿真导航器窗口增加了相应的特征树节点1D收集器Cdamp1 Collector（1）1d_manual_mesh（2），通过编辑显示修改颜色并默认文本符号（DP）的显示，如图8所示。

比较图7和图8可以看出：从实质来看两者是等效的，而从图形角度来看，两者是有区别的，当然可以借助RBE2（1D刚性梁）单元，可以构建出弹簧单元和阻尼单元“并联”的效果（即上端各自一个节点，下端分享质量单元的共同/单个节点）。

3、质量-弹簧-阻尼模型参数的定义

单击仿真导航器窗口中的【1d_manual_mesh（2）】，右键并通过【网格相关数据】定义该单元属性A/B端分量均为Z；单击Cdamp1 Collector（1）右键编辑并弹出【网格收集器】对话框，单击【Cdamp属性】编辑按钮弹出【PDAMP】对话框，在【延伸粘滞阻尼】数字框中输入63，单位为N.S /m，即可完成了定义阻尼单元属性参数的操作。

说明一下，上述定义的阻尼系数为物理阻尼，也称之为名义阻尼（有量纲），但不能直接参与后续模态分析及其动力学响应分析，需要将之转换为粘滞阻尼值（本文换算为0.315，无量纲）

4、建立仿真解算方案（SOL103实特征值）并求解

新建仿真并进入Sim环境，解算方案名称修改为：Solution SOL103实特征值，求解器为默认的【Simcenter Nastran】但将解算类型切换为【SOL103实特征值】，利用约束类型中的【固定约束】对质量-弹簧-阻尼模型的上端节点进行固定，求解后进入后处理界面，加载并打开结果文件Structrual，可以看到【模态1】数据为15.9155Hz（和质量-弹簧模型求解结果一致），和理论值15.924Hz（角频率为100Hz）非常接近。

显然，该解算类型（SOL103实特征值）还不能求解该质量-弹簧-阻尼模型的阻尼频率，需要进入下面的动力学响应解算类型才能求解。

5、建立动力学响应解算方案并求解

（1）单击仿真导航器窗口特征树节点KMC_01_fem1_sim1.sim，右键新建解算过程和响应动力学，弹出【新建响应动力学】对话框并默认解算方案的名称为Response Dynamics 1，确定并查看导航器窗口中特征树节点的变化情况。

（2）同时弹出“将Nastran参数OUGCORD添加到输入板面”等的信息提示，即需要位移的模态坐标系设置为全局坐标系。编辑【Solution SOL103实特征值】模型数据，单击【参数】的【创建建模对象】按钮，在弹出的【解算参数】对话框0-P卡片名称中，找到【OUGCORD】并将其默认值切换为【GLOBAL】，确定即可。

（3）单击窗口特征树节点Reponse Dynamics 1Solution SOL103实特征值Normal Modes［1］，右键单击【编辑阻尼系数】并在弹出的对话框【粘滞（阻尼）】中输入31.5（即31.5%），【迟滞（结构阻尼）】默认为0，确定即可。

（4）单击Normal Modes［1］（正则模态），右键单击【快速查看】并打开仿真文件视图，即可出现如图9所示的（固有）频率、阻尼频率、质量和刚度等数据，这样就得到了该质量-弹簧-阻尼系统的阻尼（固有）频率为15.11Hz，略小于固有频率15.92Hz（15.9155Hz），关闭仿真文件视图。

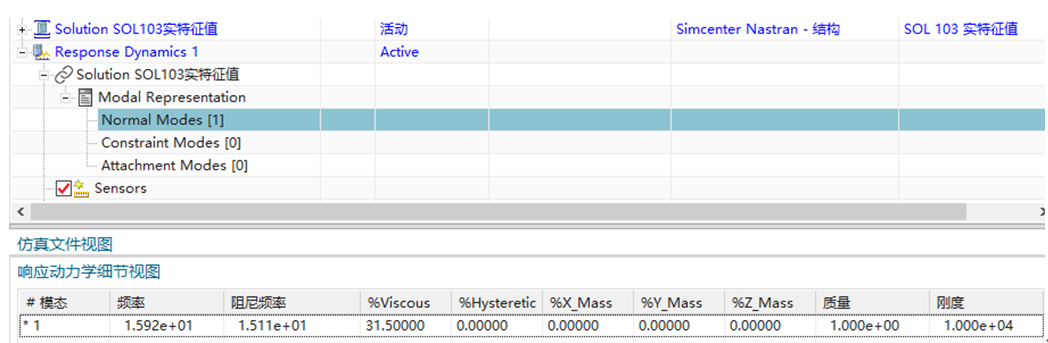
图9 正则模态相关数据

（5）资源条选项中切换为【XY函数导航器】，单击【f（x）数学函数】右键创建弹出对话框，【用途】切换为【响应动力学】，默认函数类型为时间，函数定义名称修改为：data_func01，【轴单位设置】的【X类型】为默认，【Y类型】切换为【力】和单位为【N】，默认【预览区域】中的X向增量为0.01、点数为1024，即这两个参数决定了整个响应的时间大小为10.24s。在公式列表中输入2000*sin（100*time），检查公式的语法并确定，即可在【XY函数导航器】窗口特征树增加了data_func01，可以对此进行绘图输出便于查看该函数是否合理。

（6）单击data_func01，右键导出弹出【导出文件】对话框，默认文件类型为默认的.afu，并定义目标文件，选择电脑的某个目录并命名该函数文件名为F2000并确定。

（7）资源条选项中切换为【仿真导航器】，单击Reponse Dynamics 1右键新建事件，在弹出的对话框中默认类型为【瞬态】，默认名称为Event_1，默认【事件属性】，初始条件切换为【零】，确定即可。

（8）单击窗口新出现的特征树节点Event_1Excitations新建激励平移节点并弹出【新建平移节点激励】对话框，默认名称，选中图形窗口模型上质量所在的节点（必要时单击【回到主页】图标），在激励函数中勾去【X】和【Y】方向选项，单击【Z】条框的箭头符号并单击弹出的【f（x）函数管理器】，在弹出的对话框中选中已经创建的F2000.afu函数，确定即可。

（9）单击Event_1并右键单击【求解模态响应】即可完成了动力学响应计算。

6、质量-弹簧-阻尼结果查看

单击Event_1，右键并单击评估函数响应节点，弹出【计算节点函数响应】对话框，结果类型为默认的【位移】，节点选择模型中质量所在的节点，响应请求的数据分量切换为【Z】，确定后即可在窗口出现位移随时间变化的曲线图，通过【编辑轴】将时间最大值设定为1s，即可出现如图10所示的位移变化曲线图。

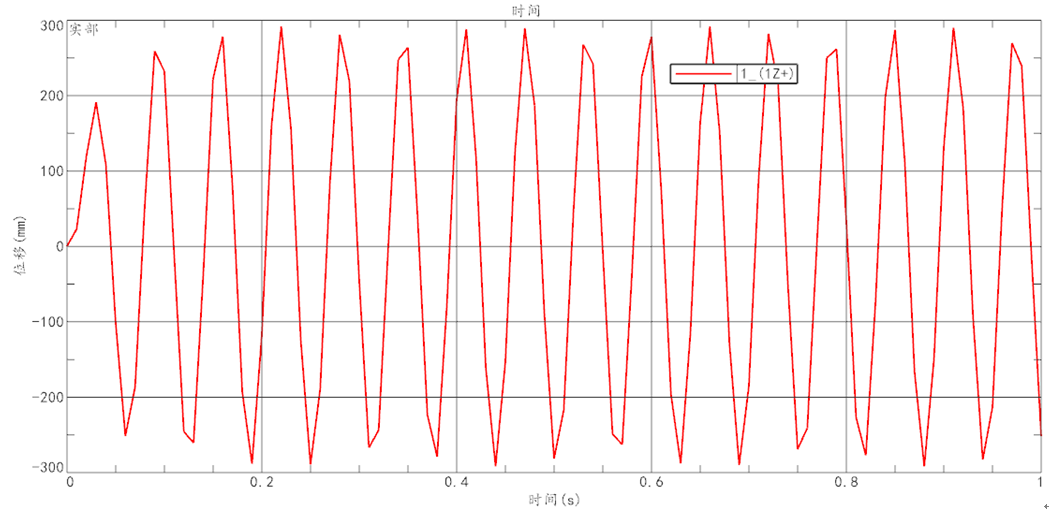
图10 位移变化曲线图

四、总结和讨论

（1）在建立上述单自由度质量-弹簧-阻尼模型并求解谐响应基础上，可以改变激励频率、粘滞阻尼（无量纲）和激振力最大幅值等参数，或者改变激励力的函数类型，通过仿真可以得到质量点不同的位移曲线图。

（2）在掌握了单自由度质量-弹簧-阻尼模型构建方法的基础上，可以构建更复杂的两自由度、多自由度质量-弹簧-阻尼模型并进行其他瞬态、频率、随机振动、冲击和响应谱等动力学响应事件并做相应的分析。

另外，说一下本人多年来学习CAE心得和CAE教学的经验：CAE学习方法和学习效果因人、因专业各异，但基础建模的训练和对比学习方法，一定是进入CAE门槛的共性方法和必经之道，建议初学者集中精力通过专题学习（例如本文的质量-弹簧-阻尼建模）达到一定的技能和应用水平。

审核编辑 ：李倩