

盛最多水的容器:双指针的经典题目
描述
大家好,我是吴师兄,
今天的题目来源于 LeetCode 第 11 号问题:盛最多水的容器,难度为「中等」,属于双指针的经典题目。
一、题目描述
给你 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
二、题目解析
一开始,我们先去考虑相距最远的两个柱子所能容纳水的面积。
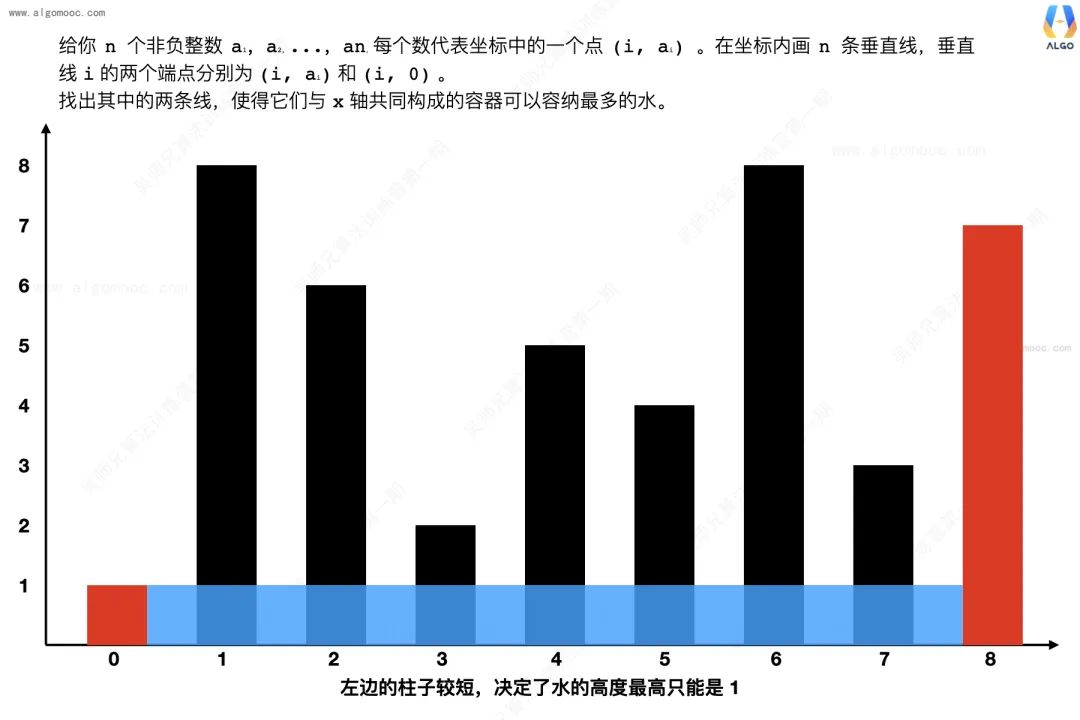
接下来去思考,我们去移动哪根柱子会更加合适?
这里我们需要注意一点:无论移动哪根柱子,柱子之间的宽度都是变小的。
移动右边那根更高的柱子?
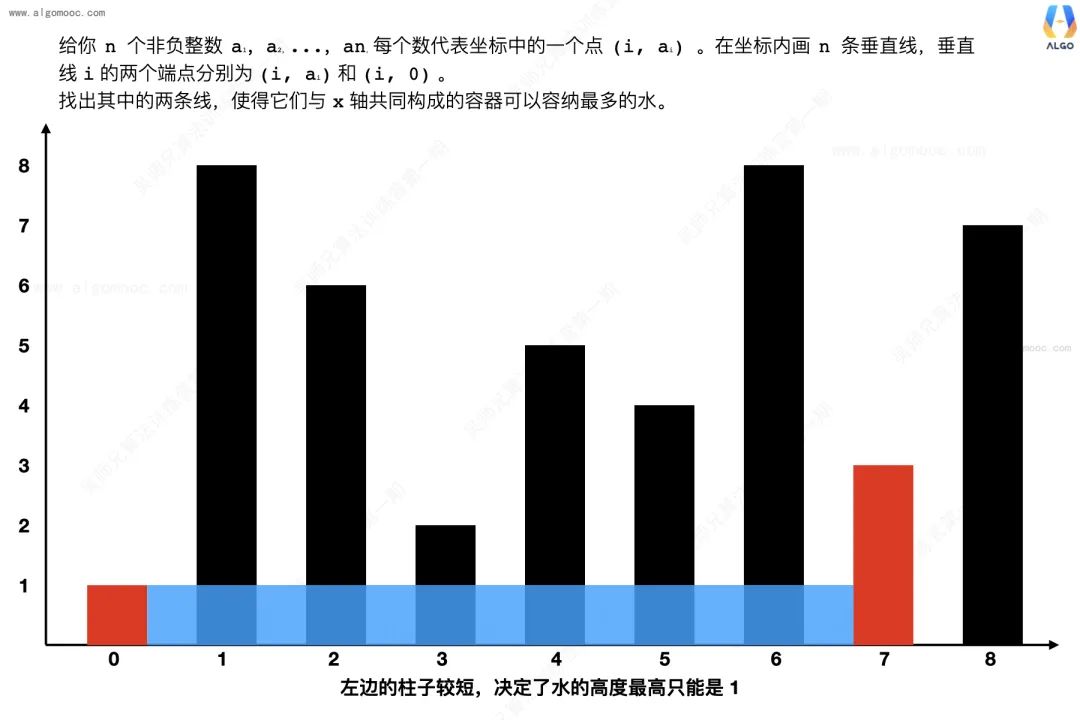
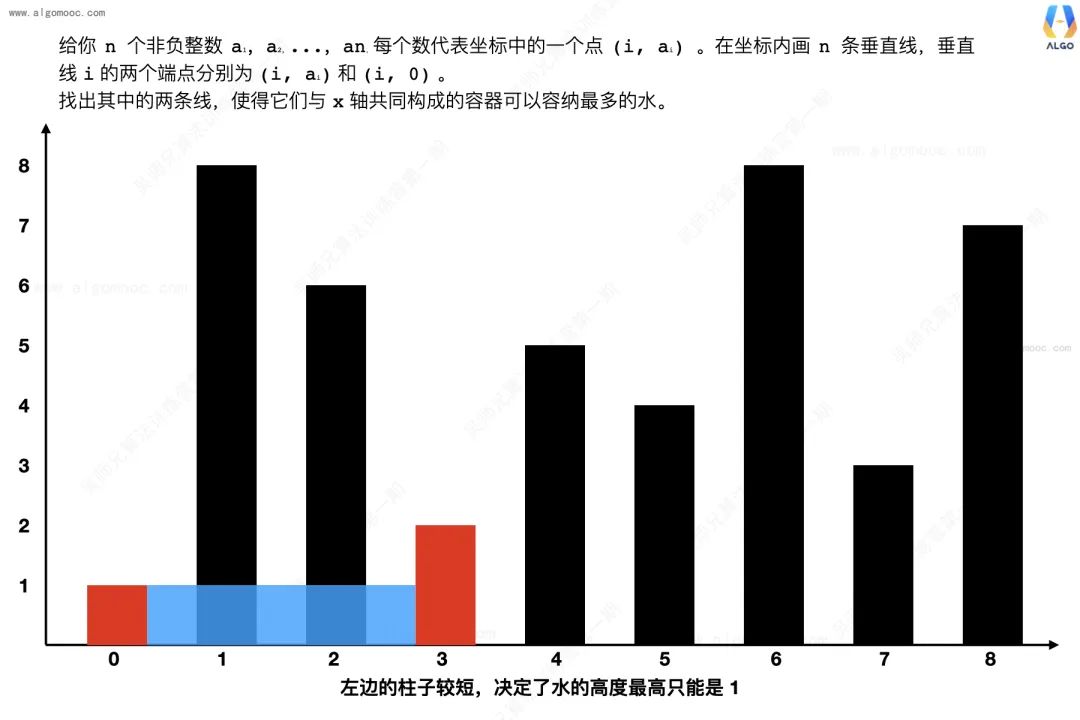
由于水面高度是由最短的柱子决定的,所以移动右边那根更高的柱子的时候,水面高度一定是不会增加,甚至有可能遇到更短的柱子而变小,而宽度有一定再减少,所以水的面积也一定减少。
移动左边那根更短的柱子?
这时候,水的高度是不确定的,那么面积也是不确定的,有可能比之前更大,也有可能更小或者相等。
所以,我们可以得出一个结论:移动两根柱子之间更短的那根柱子,才有可能在宽度一定变小的情况下,找到一个更高的水面,从而使得面积有可能更大。
那接下来这道题目的解法也就有了:
1、设置两个索引,分别指向容器的两侧,即索引 left 指向最左边的柱子,索引 right 指向最右边的柱子。
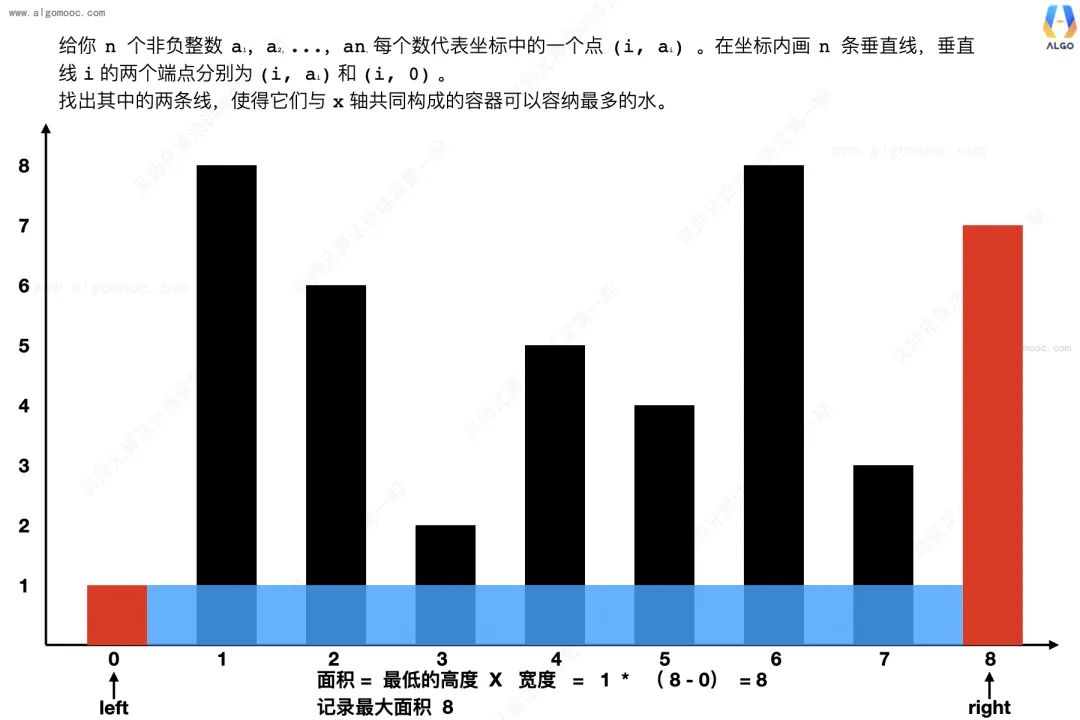
2、记录下此时的水的面积,可以定义为 res
3、观察需要向内移动哪根柱子
- 1)如果移动较高的柱子,由于水的宽度在变小,而水的高度一定不会增加,所以最终水的面积不会超过之前记录的水的面积 res
- 2)所以,只能移动较短的柱子,然后计算此时水的面积,再与之前记录的水的面积 res 进行比较,保存那个更大的值
4、再去判断应该向内移动哪根柱子
5、直到 left 和 right 相遇为止
三、参考代码
1、Java 代码
// 登录 AlgoMooc 官网获取更多算法图解
// https://www.algomooc.com/587.html
// 作者:程序员吴师兄
// 代码有看不懂的地方一定要私聊咨询吴师兄呀
// 盛最多水的容器 ( LeetCode 11) : https://leetcode-cn.com/problems/container-with-most-water/
class Solution {
public int maxArea(int[] height) {
// 设置两个索引,分别指向容器的两侧
// 索引 left 指向最左边的柱子
int left = 0;
// 索引 right 指向最右边的柱子
int right = height.length - 1;
// 设置一个变量用来保存当下水的最大面积
int res = 0;
// 移动 left 和 right,直到 left 和 right 相遇为止
while(left < right){
// 水的宽度是 right - left
int width = right - left;
// 水的高度由两根柱子最短的那根决定
int h = Math.min(height[left],height[right]);
// 计算此时水的面积
int area = width * h;
// 如果此时水的面积大于了我们之前保存的那个值,我们需要更新一下
if(area >= res){
// 更新 res 的值为 area,确保 res 一直都是最大的值
res = area;
}
// 接下来去观察需要移动哪根柱子:必定是最短的那根柱子
// 如果左边的柱子更短,那么向内移动左边的柱子,因为只有这样,才有可能找到一个更高的水面
// 在宽度一定变小的情况下,水的面积才有可能增大
if(height[left] < height[right]){
// 向内移动左边的柱子
left++;
// 如果右边的柱子更短,那么向内移动右边的柱子,因为只有这样,才有可能找到一个更高的水面
// 在宽度一定变小的情况下,水的面积才有可能增大
}else{
// 向内移动右边的柱子
right--;
}
}
// 最后返回最大的面积 res 即可
return res;
}
}
2、C++ 代码
// 登录 AlgoMooc 官网获取更多算法图解
// https://www.algomooc.com/587.html
// 作者:程序员吴师兄
// 代码有看不懂的地方一定要私聊咨询吴师兄呀
// 盛最多水的容器 ( LeetCode 11) : https://leetcode-cn.com/problems/container-with-most-water/
class Solution {
public:
int maxArea(vector<int>& height) {
// 设置两个索引,分别指向容器的两侧
// 索引 left 指向最左边的柱子
int left = 0;
// 索引 right 指向最右边的柱子
int right = height.size() - 1;
// 设置一个变量用来保存当下水的最大面积
int res = 0;
// 移动 left 和 right,直到 left 和 right 相遇为止
while(left < right){
// 水的宽度是 right - left
int width = right - left;
// 水的高度由两根柱子最短的那根决定
int h = min(height[left],height[right]);
// 计算此时水的面积
int area = width * h;
// 如果此时水的面积大于了我们之前保存的那个值,我们需要更新一下
if(area >= res){
// 更新 res 的值为 area,确保 res 一直都是最大的值
res = area;
}
// 接下来去观察需要移动哪根柱子:必定是最短的那根柱子
// 如果左边的柱子更短,那么向内移动左边的柱子,因为只有这样,才有可能找到一个更高的水面
// 在宽度一定变小的情况下,水的面积才有可能增大
if(height[left] < height[right]){
// 向内移动左边的柱子
left++;
// 如果右边的柱子更短,那么向内移动右边的柱子,因为只有这样,才有可能找到一个更高的水面
// 在宽度一定变小的情况下,水的面积才有可能增大
}else{
// 向内移动右边的柱子
right--;
}
}
// 最后返回最大的面积 res 即可
return res;
}
};
3、Python 代码
# 登录 AlgoMooc 官网获取更多算法图解
# https://www.algomooc.com/587.html
# 作者:程序员吴师兄
# 代码有看不懂的地方一定要私聊咨询吴师兄呀
# 盛最多水的容器 ( LeetCode 11) : https://leetcode-cn.com/problems/container-with-most-water/
class Solution:
def maxArea(self, height: List[int]) -> int:
# 设置两个索引,分别指向容器的两侧
# 索引 left 指向最左边的柱子
left = 0
# 索引 right 指向最右边的柱子
right = len(height) - 1
# 设置一个变量用来保存当下水的最大面积
res = 0
# 移动 left 和 right,直到 left 和 right 相遇为止
while left < right :
# 水的宽度是 right - left
width = right - left
# 水的高度由两根柱子最短的那根决定
h = min(height[left],height[right])
# 计算此时水的面积
area = width * h
# 如果此时水的面积大于了我们之前保存的那个值,我们需要更新一下
if area >= res :
# 更新 res 的值为 area,确保 res 一直都是最大的值
res = area
# 接下来去观察需要移动哪根柱子:必定是最短的那根柱子
# 如果左边的柱子更短,那么向内移动左边的柱子,因为只有这样,才有可能找到一个更高的水面
# 在宽度一定变小的情况下,水的面积才有可能增大
if height[left] < height[right] :
# 向内移动左边的柱子
left += 1
# 如果右边的柱子更短,那么向内移动右边的柱子,因为只有这样,才有可能找到一个更高的水面
# 在宽度一定变小的情况下,水的面积才有可能增大
else:
# 向内移动右边的柱子
right -= 1
# 最后返回最大的面积 res 即可
return res
四、复杂度分析
时间复杂度:O(N),双指针总计最多遍历整个数组一次。
空间复杂度:O(1),只需要额外的常数级别的空间。
审核编辑 :李倩
-
大家来说说Altium Designer除了6.9版比较经典外,目前哪个版本最经典,使用人数最多?2017-05-28 13552
-
C语言 经典面试题目2017-08-05 5836
-
汽包平衡容器原理知识分享2018-01-07 12173
-
浅析RT-Thread中对象容器与双链表的操作2022-05-18 2296
-
经典著作《C和指针》2014-09-11 854
-
C语言_指针总结_经典讲解2016-01-06 695
-
C和指针_C与C++经典著作2016-11-16 1064
-
C语言经典面试题目2017-01-05 979
-
C指针详解-经典-非常详细2017-10-23 2082
-
100例C语言经典算法题目和实例程序免费下载2019-10-15 1411
-
C语言指针的经典实例讲解2019-11-07 1514
-
Leetcode上第11号问题:盛最多水的容器2020-05-06 4192
-
快慢指针、左右指针的常见算法2020-11-26 2925
-
C和C++经典著作《C和指针》2022-01-17 859
-
双电层电容器的工作原理 双电层电容器的特点2024-03-07 7469
全部0条评论

快来发表一下你的评论吧 !

