

冲激信号和冲激偶信号的常用公式总结
描述
这是之前法表过的一篇旧文,当时复合冲激函数的公式中少写了一个绝对值。此处做了修订,并且增加了一些内容,重新发出。
冲激信号,是信号与系统中的一个难点,本篇对冲激信号和冲激偶信号的常用公式做了总结,并给出了几道题目。
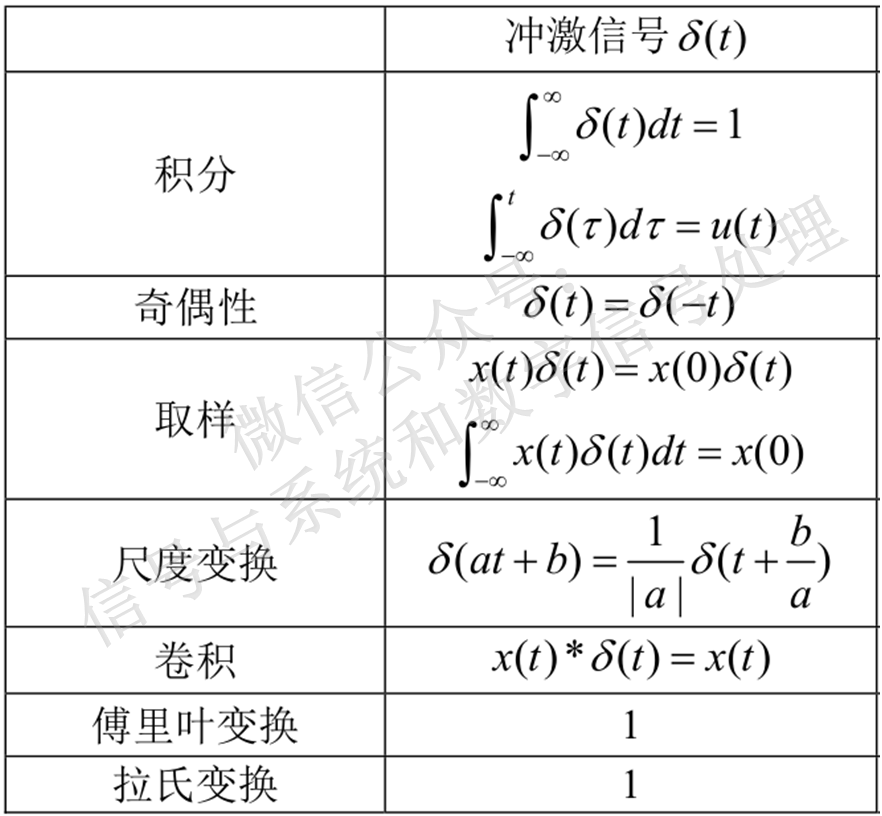
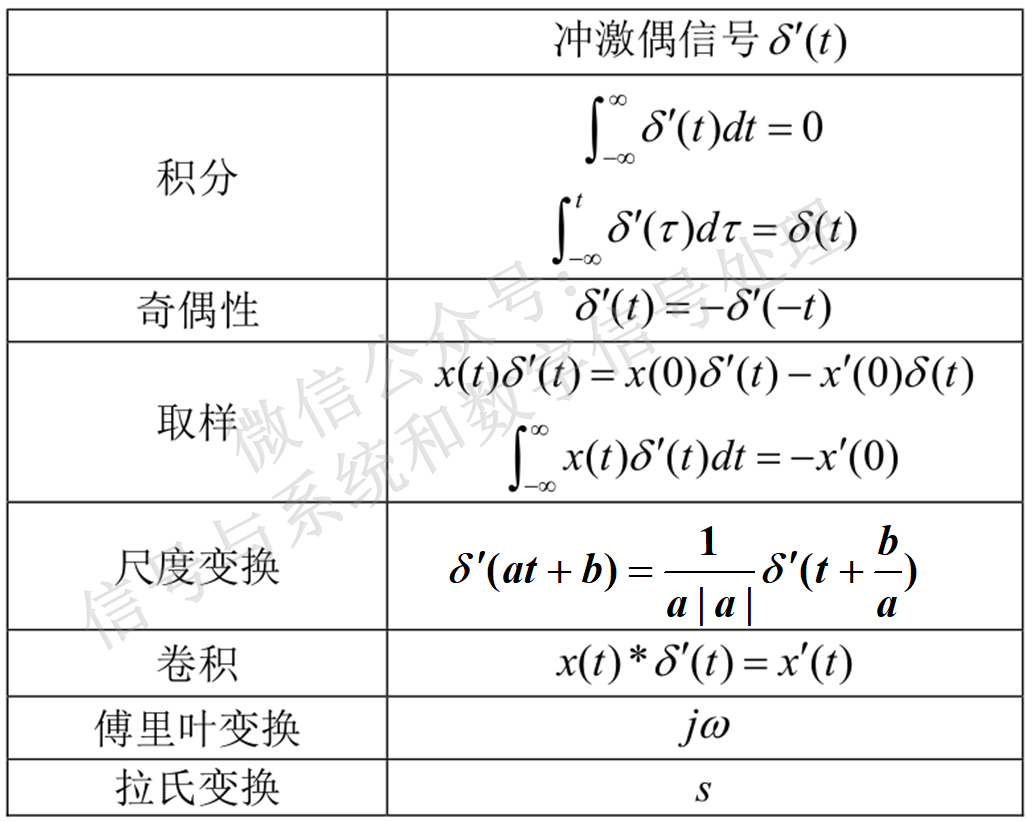
下表总结了冲激信号和冲激偶信号的常用公式。为简洁起见,本表只给出了冲激在原点处的公式,对于t替换为t-t0的性质描述不再赘述。
冲激偶的取样特性,可以由冲激信号的取样特性推导出来。推导过程如下:
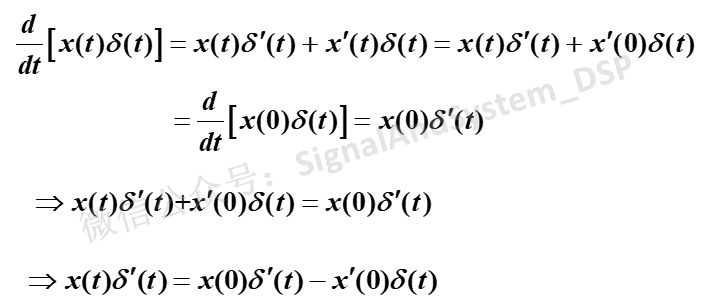
从上式出发,等式两边取积分:
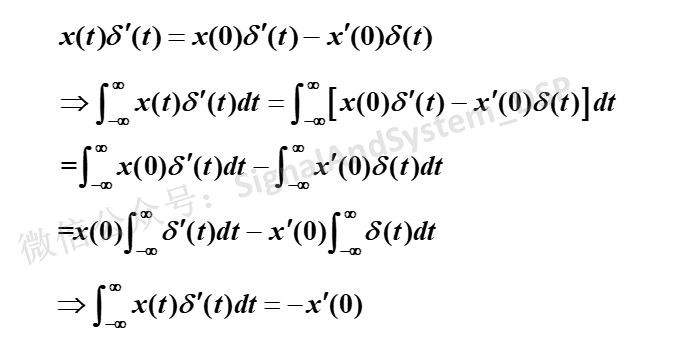
冲激信号的展缩特性应用较多,冲激偶信号的展缩特性应用较少,展缩特性的证明,可见以下链接:
https://blog.csdn.net/weixin_44252933/article/details/123654783
下面给出几道典型题目。

答案如下:

上例中的(2)(3)两题很有代表性,也是常见题型,总结如下:

再来说一下第(5)题,有两种方法:
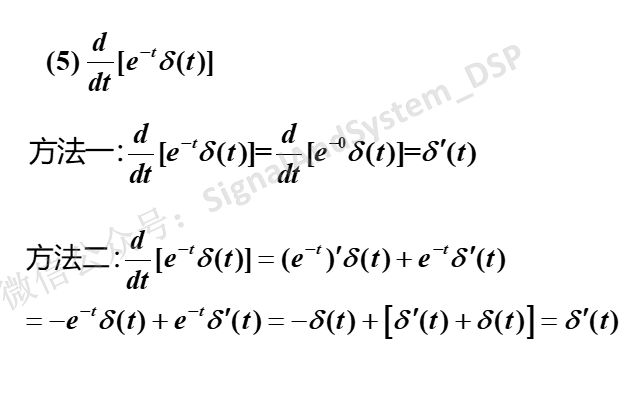
冲激函数的题目中,还有一类比较难的,就是“复合冲激函数”,公式如下:

冲激函数的尺度变换特性,可以看作复合冲激函数的一个特例,大家可以自行验证。
上述公式见郑君里《信号与系统》(第二版)上册P77,值得注意的是,在郑老先生的第三版中,删除了这部分内容。
冲激函数,在信号与系统中非常重要,但是复合冲激函数与信号与系统可以说关系不大。可是,在考试特别是考研中它像一个幽灵一样不时冒出来吓唬大家,因为有些老师喜欢出这方面的题目。下面就给一道。
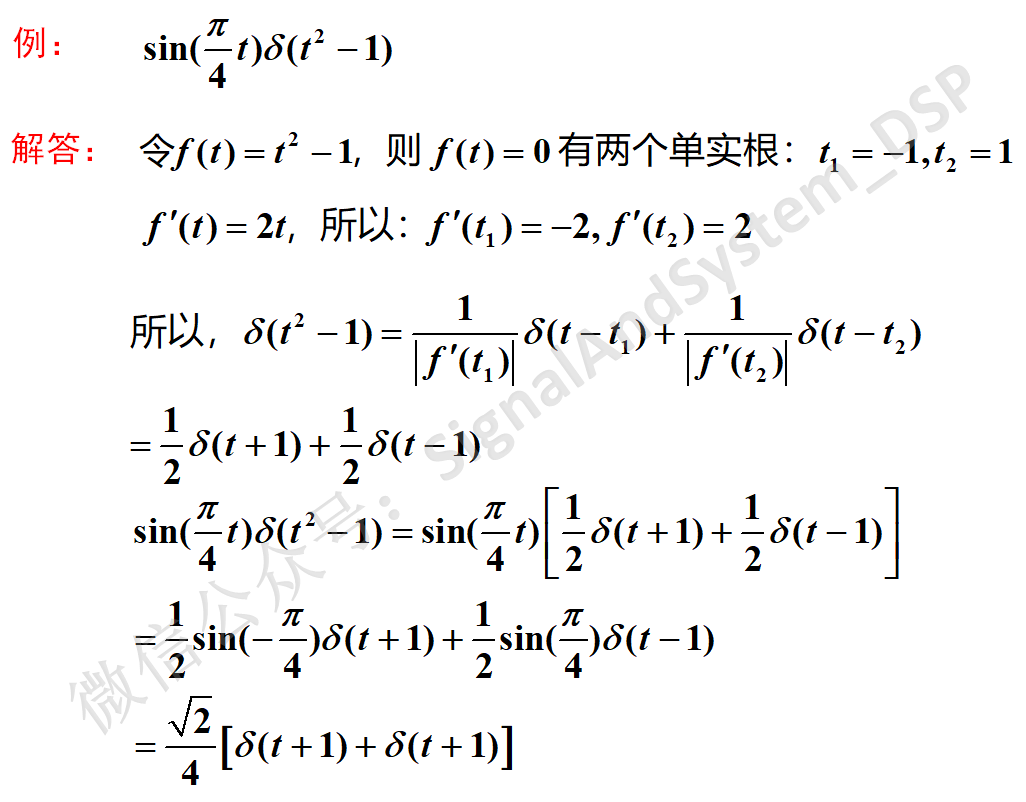
再给一道:

这是我最后要特意强调的:


审核编辑 :李倩
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
电容过压发热爆炸的原理——冲激电流信号2020-11-29 11193
-
使用激光雷达研究脉冲激光回波信号特性对探测性能有怎么样的影响2019-12-24 1608
-
冲激雷达接收的随机射频干扰问题怎么解决?2019-08-21 1819
-
冲激雷达系统的射频干扰有什么办法抑制?2019-08-20 2016
-
脉冲激光能量参数关系_脉冲激光器的能量换算2018-05-17 26108
-
LabVIEW冲激信号的频谱分析2018-05-14 4829
-
阶跃信号和冲激信号2017-12-06 527
-
阶跃信号和冲激信号.zip2017-10-04 1374
-
阶跃信号和冲激信号.ppt2017-10-03 1688
-
信号与系统郑君里ppt课件 (下载)2009-09-30 2432
-
冲激响应和阶跃响应2009-09-10 2874
-
阶跃信号与冲激信号2009-09-08 714
-
阶跃函数和冲激函数2009-07-27 15055
-
脉冲激光电源的设计与研制2009-07-15 2352
全部0条评论

快来发表一下你的评论吧 !

