基于超宽带传感器和惯性测量单元融合的定位算法

据麦姆斯咨询报道，为了解决非视距（Non-Line-of-Sight，NLOS）影响下，单一传感器的室内定位问题，来自深圳大学和国家无线电监测中心的研究人员提出了基于超宽带（Ultra-Wide Band，UWB）传感器和惯性测量单元（Inertial Measurement Unit，IMU）融合的定位算法，实现在NLOS场景下的高精度室内定位系统。相关研究成果以论文形式发表于《无线电工程》期刊。

定位系统描述

基于自组织的分布式网络管理模型如图1所示，主要由3部分组成：网管服务器、分布式网络代理（Distributed Network Agent，DNA）和被管设备。

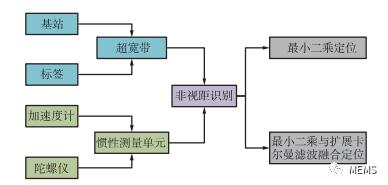
图1 自组织的分布式网络管理模型

此外，IMU传感器中的陀螺仪通过姿态矩阵进行姿态解算，加速度计通过二次积分获得位置信息。UWB通过基站与标签之间的通信解算出位置信息。通过当前位置和UWB测得的距离信息采用支持向量机（Support Vector Machine，SVM）进行NLOS信号的识别分类。

NLOS信号的检测

虽然UWB技术具有较强的抗干扰能力和抗多径衰弱能力，但是在NLOS情况下，UWB信号的测距定位能力将大大降低。因此在进行UWB定位时，要进行NLOS的识别。在双向测距（Two-way Ranging，TWR）的解算过程中，脉冲信号一共传递了3次。当出现障碍物遮挡时，信号的传输会多次受到NLOS的影响，相比于前一时刻的信号传播时间会出现较大的跳变。因此，研究人员提出使用机器学习的方式，利用支持向量机（Support Vector Machine，SVM）对实际场景中的NLOS和LOS情况下的距离测量值进行训练，得到符合对应应用场景的分辨阈值。由于移动障碍物可能会对UWB系统的NLOS测距结果产生规律性的影响，因此通过设置障碍物的位置模拟NLOS场景，并研究障碍物位置与NLOS检测之间的关系。NLOS/LOS样点采集模型如图2所示。

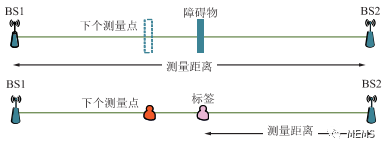
图2 NLOS/LOS样点采集模型

IMU和UWB融合定位仿真实验

为了验证所提出的算法的性能，研究人员通过仿真实验进行模拟。在不同观测噪声下，通过最小二乘法（Least Squares Method，LS）和LS-扩展卡尔曼滤波（EKF）算法的定位轨迹如图3（a）所示。在同等观测噪声下，UWB和IMU经过EKF滤波过后的定位轨迹要比只经过LS定位算法的定位轨迹数据抖动更小，轨迹更加平滑。且观测噪声也会对定位结果有较大影响。图3（b）显示了2种算法的误差变化趋势。在观测噪声R=0.1时，经过LS算法定位的轨迹误差在0.1-1.4m抖动，经过EKF滤波后定位误差下降并逐渐保持稳定在0.2-0.4m。在观测噪声R=0.01时，LS-EKF算法的误差明显要比LS算法平滑得多，且定位误差更小。图3（c）是2种算法对应的误差累计分布函数（Cumulative Distribution Function，CDF）图，在观测噪声R=0.1时，LS和LS-EKF算法在仿真的数据范围内的最大误差分别为1.3m和0.85m；在观测噪声R=0.01时，LS和LS-EKF算法在仿真的数据范围内的最大误差分别为0.3m和0.2m。

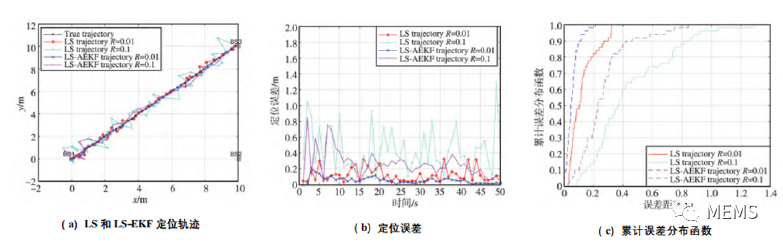
图3 LS和LS-EKF定位算法

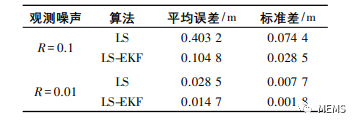
LS和LS-EKF算法平均误差和标准差如表1所示，在观测噪声R=0.1时，LS和LS-EKF算法平均误差为0.4032m和0.1048m，误差的标准差大小为0.0744m和0.0285m。在观测噪声R=0.01时，LS和LS-EKF算法平均误差为0.0285m和0.0147m，误差的标准差大小为0.0077m和0.0018m。在观测噪声分别为R=0.1和R=0.01时，相较于LS算法，LS-EKF算法的定位精度分别提高了74%和48%。因此，所提出的算法能很好地识别和缓解NLOS带来的定位误差。

表1 LS和LS-EKF算法平均误差和标准差

　　

      审核编辑：彭静