讲讲与、或、非门都能用来做什么

上次介绍了与、或、非门。这次我们讲讲这些门能用来做什么。

 《加法器》（实现两数相加）

我们考虑以下几种情况（以下数字皆为二进制数）。

0+0=0 零加零毫无疑问等于0。

0+1=1   1+0=1 这个应该也不用解释。

1+1=10  2的二进制数写作10，所以也没有什么问题。

我们可以绘制出这样一张表。其中A和B为输入（加数），C（和）和D（进位）为输出。

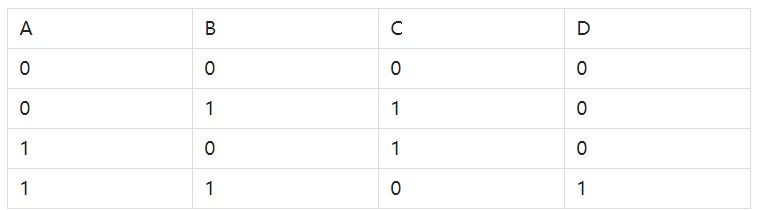
我们可以用以下电路来满足这张表（真值表）

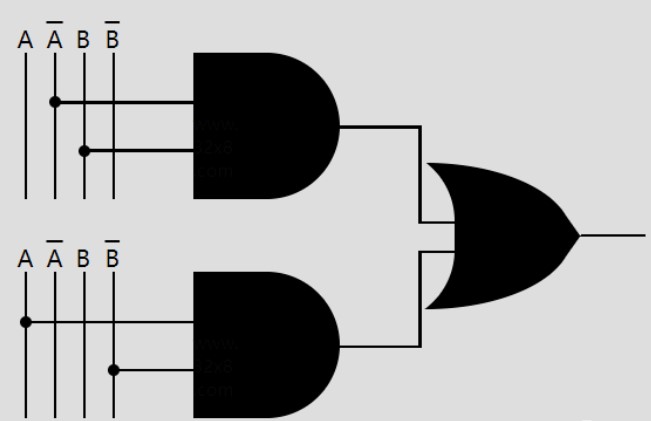
 解释一下，A上有一条横线则意为A的取反。如果A是0，那么A-就是1。最右边的则是C本位求和输出。本图中没有D输出，D输出放在下图中讨论。我们来试一下真值表的第一行。

 第一行中A和B数值均为0，A-为1，故第一路与门输出为0，同理第二路输出也为0。两条与门输出作为或门的输入，故与门的输出也为0。剩下的几行你们可以自己试试看。

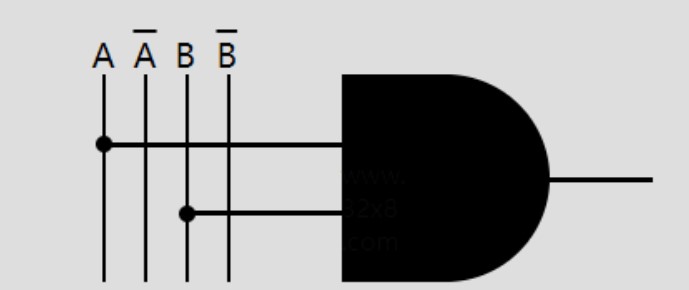
这张图是D的进位输出。可以从真值表很容易观察得到D与A和B的关系就是与门的关系，所以很容易画出这个电路。

既然本位相加和进位信号都有了，那么我们便可以设计出下图这样的加法器：
 

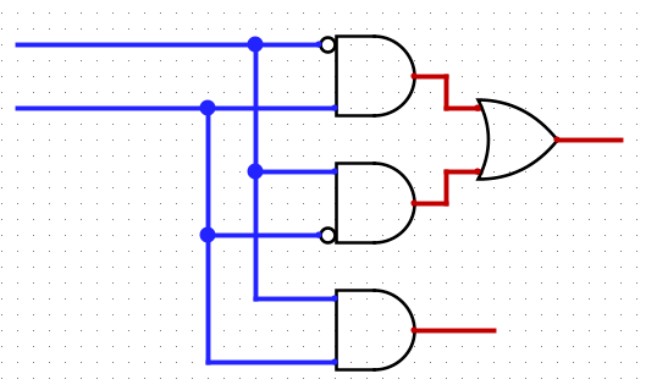
左边两根蓝线从上至下分别是A和B输入。右边两根红线从上至下分别是C和D输出。

这个电路被称为半加法器。如果我们要算的数值有三位，那么我们就串联三个这样的电路就可以实现四位的加法。注意不是简单串联，本位的进位要与下一位的和相加。
 

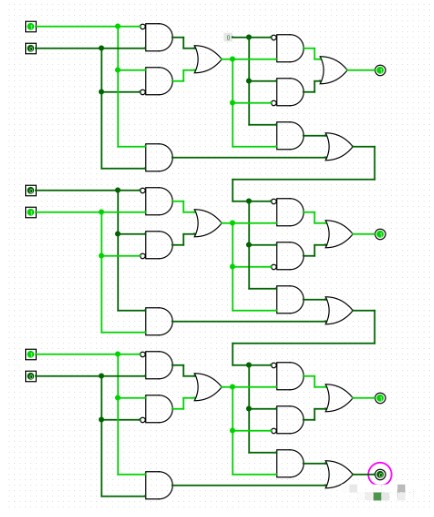
这是三位加法器，其中加数分别是101（5）和10（2），和是111（7）右下角粉红圈中的是溢出信号（最高位的进位信号），第一位数字没有前一位的进位信号，所以你可以在图中的上半部分看到一个特别的常数0。注意：不要将该电路误解成并联，其实质还是串联。你们可以跟着门电路和二进制加法琢磨琢磨其本质。

其中减法比较巧妙，它在加法的基础上稍加改动而来。

比如101（5）-010（2）=011（3）我们把减数010按位取反，变成101，再在末尾加1，变成110。我们发现101+110=1011，若把最高位的数字舍去，剩下的便是差011。

再例如110110(54)-100100(36)=010010(18)。100100按位取反，变成011011，加1，变成011100。110110+011100=1010010，最高位舍去，得010010（18）。

你们可以随便写几个数试试，感受一下这个方法的巧妙之处。

不单单是加减运算，逻辑门还可以实现乘除、开方、指对等运算，可以胜任图像处理、数据检索、人工智能等任务。

重头戏还在后头呢。



审核编辑：刘清