

如何调试一个矩形微带贴片天线
描述
摘要:
微带贴片天线是由介质基板、地板、贴片导体层等组成,通常采用微带线(侧馈)或者同轴线(背馈)馈电。该类型天线因具有易于与平面电路集成以及制造成本低等特点而得到广泛应用。本次推文将简述如何调试一个矩形微带贴片天线。
1、两种理论分析方法
对于微带贴片天线,大部分教材都详细讲解了传输线分析法和腔模理论分析法,前者将辐射源等效为相距L的两个辐射槽,这种分析方法主要适用于矩形贴片;后者假设贴片和地板之间的纵向场恒定(当基板厚度远小于工作波长时),将场求解问题简化为二维边值问题(贴片和地板为电臂,腔体四周为磁臂),因此可用于各种规则贴片的求解。
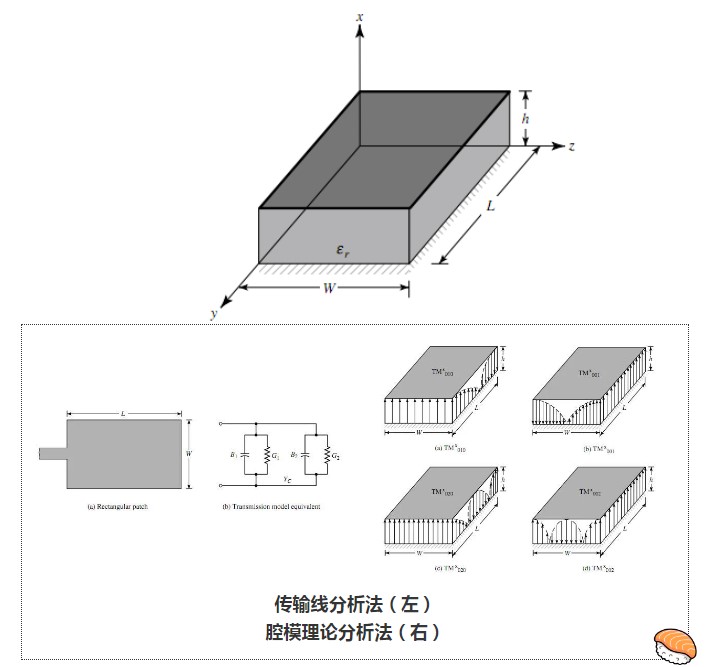
对于下面三种类型的微带贴片的求解,传输线分析法显然是无能为力的。如果不借助于电磁仿真软件,那么腔模理论分析法就可以派上用场了。
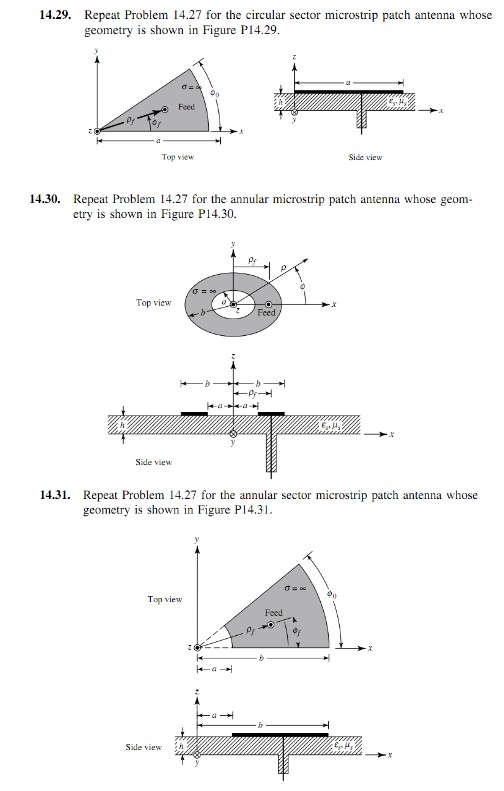
根据模型选择好合适的坐标系(直角坐标系,柱坐标系等),将电场和磁场分量用磁矢量位进行表示,找出边界条件。求解齐次波动方程的关键就是利用数学物理方程中的分离变量法求出通解,然后结合边界条件定波数,最后的场分布可由无数组正交基函数(常用的正交基函数有正余弦函数,贝塞尔函数或勒让德函数)叠加组成。
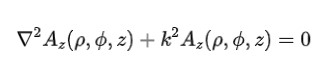
柱坐标系下的齐次波动方程
2、尺寸设计依据
对于生活中常用的矩形微带贴片天线,网上也有相应的贴片天线计算器供使用,无外乎套用下面的计算公式(参考推文贴片天线的HFSS和CST仿真对比),输入天线的工作频率,基板的介电常数和厚度即可自动计算出矩形贴片天线的长、宽尺寸。

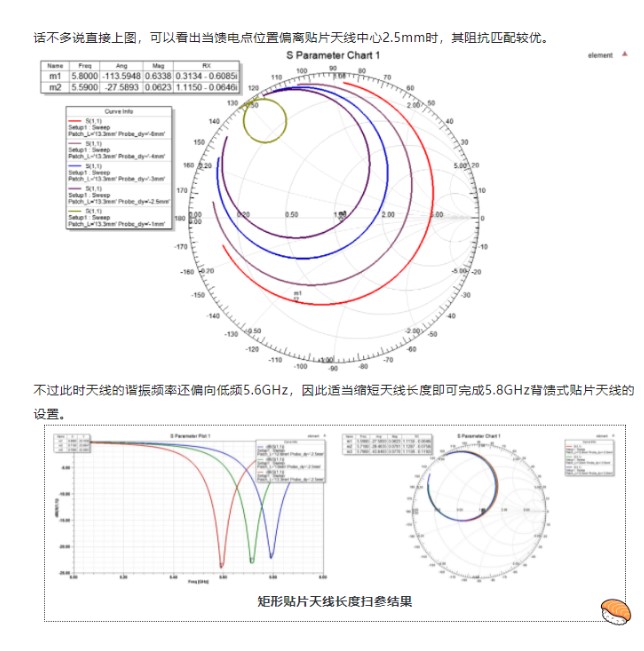
对于背馈的矩形微带天线,我们为了避免激发其他模式影响交叉极化,一般馈电点的位置选取在沿着x轴方向的宽边中心。此时需要调试Probe_dy这个参量(即馈电探针与贴片中心的纵向距离)以及馈电探针的粗细(高频时对阻抗匹配比较敏感)。
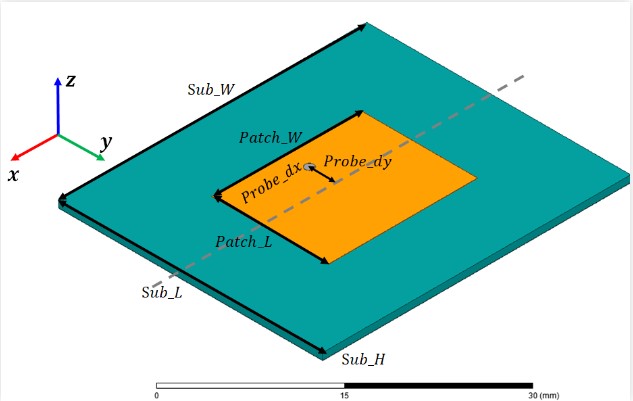
对于主模TM010而言,由于其电场在中心处最小、两边最大,因此天线的输入阻抗从中心点到两侧会逐渐变大。输入阻抗等于50Ω的馈点位置(Probe_dy)则可由下面公式简单计算得到(右滑公式可看完整版):
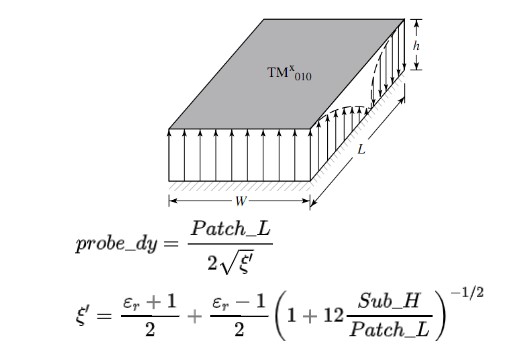
理论公式并非万能,阻抗匹配最优位置可以在调参时用最经典的二分法去不断逼近,不过S11≤-10dB(即VSWR≤2)基本能满足实际工程需求。
对于侧馈的矩形微带天线,主要是调节1/4波长匹配枝节的宽度和长度。
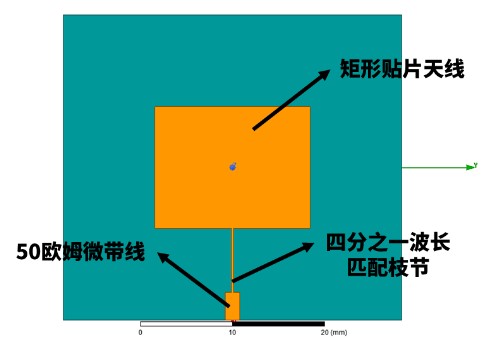
对于四分之一波长匹配枝节,其宽度取决于待匹配矩形贴片的输入阻抗,其对应的特性阻抗值满足:
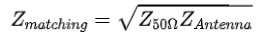
假设工作频率为5.8GHz,该频点处微带天线的输入阻抗为150欧姆,则该匹配枝节的阻抗值为86.6Ω。枝节的长度可以用txline这个工具计算得出(输入基板介电常数和厚度,微带线的阻抗值,工作频率,并设置相位为90°,即代表1/4波长):
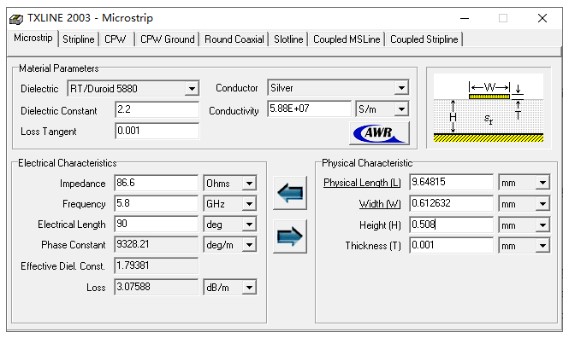
利用传输线分析法得出前面的等效电路导纳值如下所示:
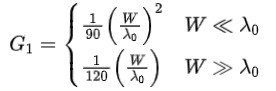
若天线谐振时不考虑两条等效辐射槽之间的互耦因素等,可以将侧馈天线的输入阻抗简化为(自由空间波长):
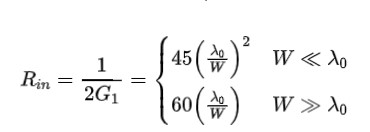
从上述公式也不难发现,宽边(非辐射边)W越大,其输入阻抗值越低;宽边尺寸过小时其输入阻抗与W呈现平方反比关系,较高的天线输入阻抗也不利于进行阻抗匹配的调试(高阻抗微带线工程实现困难)。看到这里,很多人可能会问了,为什么优先来调试匹配,而不是频偏呢?这是因为利用公式计算的贴片尺寸虽然不一定刚好在带内谐振,但是不会偏离太多。除此之外,多次扫参将这种窄带天线的阻抗匹配特性调试好后,稍微修正一下贴片的长度,即可在不影响谐振频率处阻抗匹配性能的情况下,进行天线谐振频率的搬移。
2、实调修正手段
简单的微带贴片天线属于窄带天线,很容易因为仿真精度和加工误差导致频偏和匹配恶化,因此天线实物往往需要工程师进行手动修正。这里我们简单介绍下背馈和侧馈的矩形微带贴片天线的几种实调修正手段。
背馈的矩形微带贴片天线
由于加工实物的馈电位置已经固定,因此实调时往往通过割铜皮(实际工作频率低于目标值)或者贴铜皮(实际工作频率高于目标值)的方法来进行频率修正。除此之外呢,还可以在贴片宽边边缘中心位置增加一个矩形长条(宽度为stub_W,长度为stub_L),后期用刻刀一点点割掉来修正谐振频率。
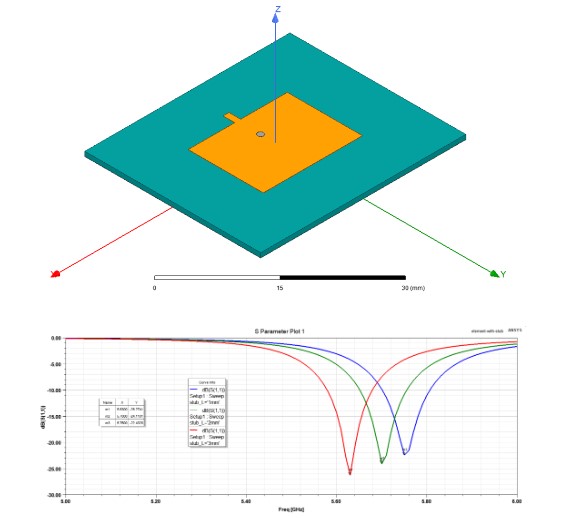
从上面的扫参分析不难看出,贴片天线的谐振频率随着矩形长条的长度减小而升高。因此可以将加工前仿真的谐振频率调试到偏向低频,实际调试时发挥割铜皮手艺,修正谐振频率至目标值即可。
侧馈的矩形微带贴片天线
对于侧馈的矩形微带贴片而言,其除了可以用割铜皮方法之外,还可以通过预留LC匹配位的方式来修正频偏和匹配(类似下图所示结构)。此时相当于是地线-信号线-地线(GSG)布局,构成了共面波导传输线馈电结构。
对于这种窄带天线而言,理论上一个L型匹配电路即可完成良好的阻抗匹配。(①先串L再并L,②先串L再并C,③先串C再并L,④先串C再并C,⑤先并L再串L;⑥先并L再串C,⑦先并C再串L,⑧先并C再串C,8种形式)。

实际使用的电容电感元件不是连续的,因此需要根据测试结果来选定合适的匹配方案。如果空间位置足够,可以选用双L匹配位,不需要的地方NC掉或者用0R电阻串过去即可,使得匹配方法更加灵活。
审核编辑:刘清
-
硅基层叠式微带贴片天线设计2022-10-13 803
-
如何调试一个矩形微带贴片天线2022-08-08 2558
-
微带天线的设计和阻抗匹配2021-06-15 1863
-
矩形微带天线的设计2021-06-08 1183
-
非辐射边共面馈电的单层矩形贴片天线的仿真及实验2020-11-24 1221
-
什么是微带贴片天线?2019-08-12 6887
-
一种具有层叠结构的双线极化方形微带贴片天线设计2019-06-12 2161
-
PBG结构的微带贴片天线设计2017-12-07 938
-
矩形切角超宽频带微带天线2010-11-10 749
-
新型光子带隙微带贴片天线2010-09-17 497
-
矩形微带天线设计2010-08-30 777
-
微带贴片背射天线的设计与分析2010-07-31 1016
-
利用接地板开槽减缩微带贴片天线的RCS2009-10-31 604
-
共面馈电凹口矩形贴片天线间的互耦2009-08-22 660
全部0条评论

快来发表一下你的评论吧 !

