

什么是高斯过程 神经网络高斯过程解析
人工智能
描述
深度诱导的神经网络高斯过程
To explore Gaussian Processes
目前,核方法和深度神经网络是两种引人注目的机器学习方法。近年来,许多理论阐明了他们的联系。
笔者曾经总结了目前理解神经网络的四个perspectives:决策边界,特征表示,把神经网络看成一个核,以及微分方程。从核的一个视角看,神经网络的一个理论进展是,“证明了在网络参数服从相同的随机初始化时,无限宽网络等价于一个高斯过程”。尽管这个理论有效而且优雅,我们注意到所有神经网络导出的高斯过程本质上都是运用了无限宽度这一假设。然而,身处深度学习时代的我们更加关心的是神经网络的深度问题,比如,增加深度如何影响网络的行为?具体地说,宽度有限无限地增加深度可以诱导出来高斯过程吗?这里笔者的一篇论文给出了肯定的答案 [1]。
——[1] Zhang, S. Q., Wang, F., & Fan, F. L. (2022). Neural network gaussian processes by increasing depth. IEEE Transactions on Neural Networks and Learning Systems
一、高斯过程
首先,我们来说明什么是高斯过程。我们对多元高斯分布很熟悉。多元高斯分布是针对一个向量,由一个平均值向量+一个协方差矩阵来定义。还记得本公众号之前的推送里面有一个高观点:“函数是无限维的向量”(高观点)。高斯过程也是高斯分布的这样一个拓展,也就是说,无限维向量的高斯分布就是一个高斯过程,高斯过程由一个平均值函数+一个协方差函数来决定。
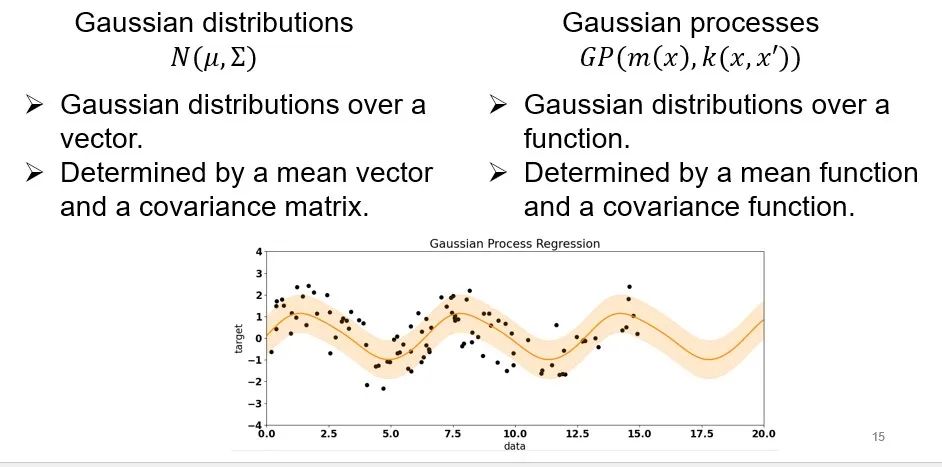
二、神经网络高斯过程
神经网络是怎么和高斯过程联系在一起的呢?Lee et al. [1] and Neal [2] 指出,随机初始化无限宽网络的参数会产生一个高斯过程,称作神经网络高斯过程(neural network Gaussian process, NNGP)。Intuitively,我们可以这么来理解这件事:给定一个参数为 i.i.d 的全连接多层网络。由于网络随机初始化,每个神经元的输出也是独立同分布。因为后面一层的每个神经元的输出是前一层所有神经元的聚合,当网络宽度无限大时,根据中心极限定理,无限多个独立同分布的变量的平均服从高斯分布。这样,网络表示的输出函数本质上是一个高斯过程,如下动态图可以很好展示这一观点。
[1] Lee, J., Bahri, Y., Novak, R., Schoenholz, S. S., Pennington, J., & Sohl-Dickstein, J. (2017). Deep neural networks as gaussian processes. ICLR.
[2] Neal, R. M. (1996). Priors for infinite networks. In Bayesian Learning for Neural Networks (pp. 29-53). Springer, New York, NY.

三、 深度诱导的神经网络高斯过程
尽管前面的NNGP理论非常优雅和有效,但它有一个重要的限制:不管网络中堆叠了多少层,NNGP之所以成功是因为网络无限宽。但是在深度学习时代,因为深度是决定深度学习力量的主要因素,我们更关心的是深度网络的深度以及深度如何影响网络的行为。因此,我们非常有必要扩大现有NNGP理论的范围,将深度纳入其中。具体来说,我们的好奇心是能否通过增加深度而不是宽度来推导出 NNGP?如果这个问题得到了肯定的回答,它将是现有理论的一个有价值的补充。由于在某种程度上存在宽度和深度之间的对称性 [1],我们认为在某些条件下加深神经网络也可能导致 NNGP。
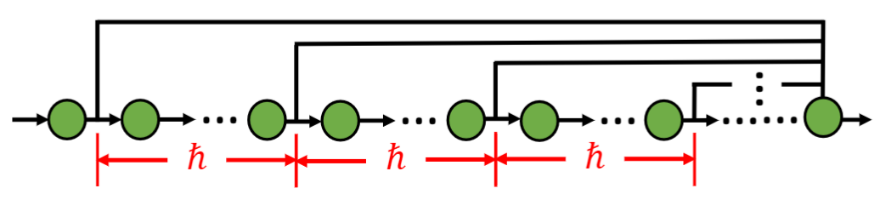
我们研究了如下图所示的网络架构。这种拓扑结构的特点是间隔hbar中间层的输出在最后一层聚合,产生网络输出。这样的网络输出会是一个高斯过程吗?虽然当网络无限深的时候,这个网络的输出也是可以无限多个变量聚合在一起,但是这些变量并不是独立的。它们是隐含层的输出,隐含层之间是有依赖关系的,因此我们不能简单的用中心极限定理。可是我们发现,当hbar很大的时候,被聚合的隐含层距离越来越远,以致于它们之间的依赖会越来越小,最后这些变量可以满足弱依赖的中心极限定理 [2]。结果也是一样的,深度诱导的高斯过程存在!
[1] Fan, F. L., Lai, R., & Wang, G. (2020). Quasi-equivalence of width and depth of neural networks. arXiv preprint arXiv:2002.02515.
[2] https://en.wikipedia.org/wiki/Central_limit_theorem
简要说下证明的思路,弱依赖里面有一种情形叫做beta-mixing,它的含义是说:一个变量的独立分布的概率和这个变量相对于另外一个变量的概率的差是很小很小(指数级别)。我们的证明就是创造条件让beta-mixing成立。为此我们初始化权重和bias使其norm都不太大,然后我们增大hbar至无穷,由于复合作用,被聚合的隐含层的输出之间影响将很小,满足beta-mixing。证明摘要如下:



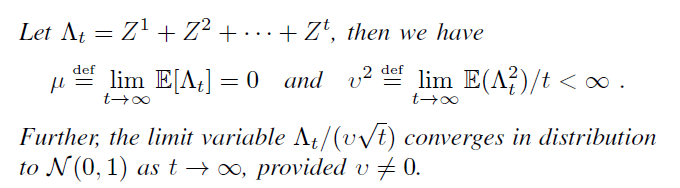

编辑:黄飞
-
PyTorch神经网络模型构建过程2024-07-10 1351
-
bp神经网络算法过程包括2024-07-04 1465
-
PyTorch教程18.1之高斯过程简介2023-06-05 652
-
高斯过程回归GPR和多任务高斯过程MTGP2021-06-30 1684
-
高斯过程隐变量模型及相关实践2021-03-11 1498
-
详解卷积神经网络卷积过程2019-05-02 19111
-
监测时间序列数据的高斯过程建模与多步预测2018-03-08 1338
-
求基于labview的BP神经网络算法的实现过程2012-12-10 8554
-
嵌入自联想神经网络的高斯混合模型说话人辨认2010-03-05 532
-
利用RBF神经网络实现高斯型函数积分2009-03-29 573
全部0条评论

快来发表一下你的评论吧 !

