估算SNR和SFDR的实际考虑因素

我们周围的世界越来越数字化，这并不奇怪。一个原因可能是数字形式的数据的操作、存储和使用比模拟形式更方便、更容易。这使得将模拟信号转换为数字形式以供进一步处理和使用的电路更加重要。

在任何电路中使用模数转换器 (ADC) 时，用户首先询问的是位数 (NOB)，然后是采样率。但有效位数 (ENOB) 将告诉您有关转换器本身的大量信息。与 ENOB 一起，采样频率、无杂散动态范围 (SFDR)、积分非线性 (INL) 和微分非线性 (DNL) 是可以指导您选择预期 ADC 的参数。

在本文中，我将讨论各种参数对动态行为的影响，包括对信噪比 (SNR) 影响最大的参数，以及 ADC 的一些静态行为。我将首先检查几个关键参数对 SNR 的影响，例如抖动、量化噪声、输入信号和 DNL。

抖动

采样时钟的不确定性导致采样电压的误差，如图1所示，描述了时钟抖动引起的采样电压误差。

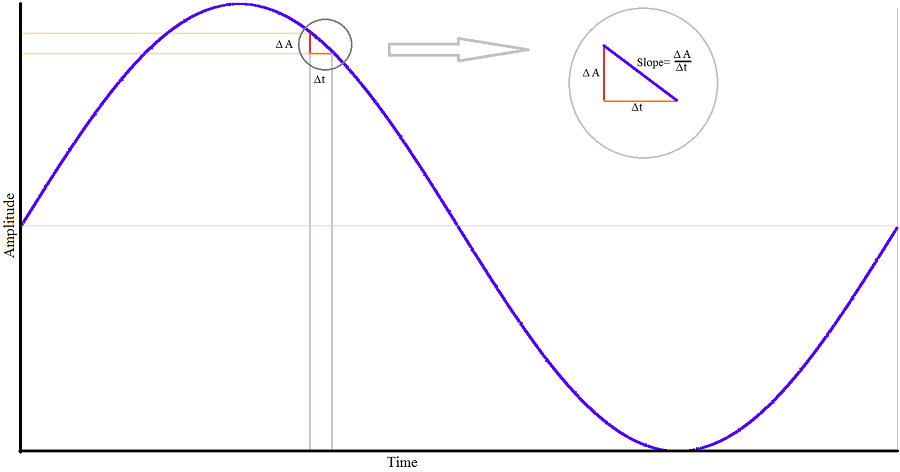
图 1：采样时钟抖动。

考虑V in = V p sin (2p f in )形式的输入信号。输入信号对时间的导数是它的变化率。最大变化发生在 cos(2p f in ) 等于 1 时，导致公式 1：

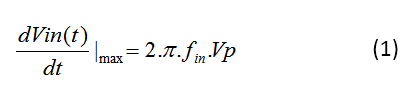
为确保具有满量程电压 (VFS) 的给定 N 位 ADC 可容忍来自抖动的电压误差 (t j )，它必须小于 V LSB /2 (等式 2)，其中V LSB 为由 VFS/2 N定义：

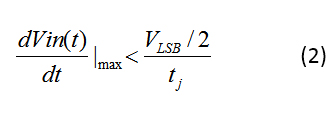
对于公式 1 中的给定正弦波，您可以使用公式 3 求解抖动 (tj)：

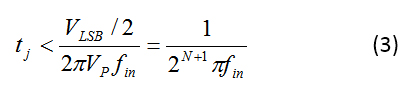
我使用 V p-p = V FS 和V p = 2 N–1 V LSB 来重写方程。

对于输入频率为 80 MHz 的 12 位 ADC，抖动必须小于 485 ps 才不会导致采样错误。

现在让我们看看抖动对 ADC SNR 的理论影响。如果 V e-RMS是输入正弦波的 t j的最坏情况均方根 (RMS) 电压误差，则公式 4 为：

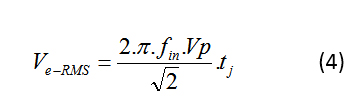
公式 5 将抖动误差对 SNR 的贡献表示为：

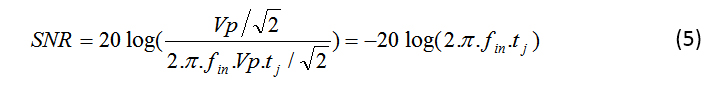
量化噪声

 

由于 ADC 代表给定代码的不同模拟输入范围，因此每个数字代码必然会出现错误。简而言之，尽管为给定代码分配了一系列模拟输入，但对于给定代码，只有一个模拟输入被准确表示。因此，与给定模拟输入的分配代码相关联的错误。该误差的范围可以从 –LSB/2 到 +LSB/2。

例如，在图 2中，2.5 到 3.5 范围内的所有模拟输入都用相同的数字代码表示：0 … 011。

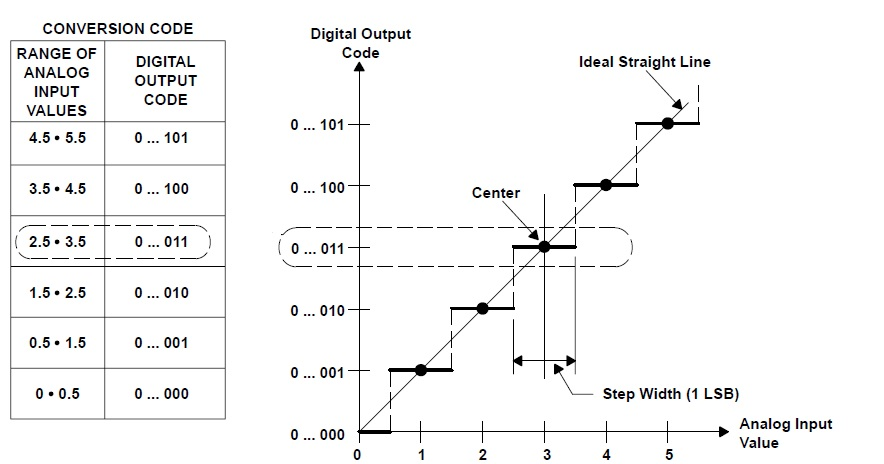
图 2：ADC 的理想传递函数。

此范围内的每个输入在范围边界处都有较大的误差（具有不同的极性）；当您靠近范围的中心时，误差会变小。绘制量化误差与模拟输入范围的关系图会得到众所周知的锯齿图，如图3 所示。

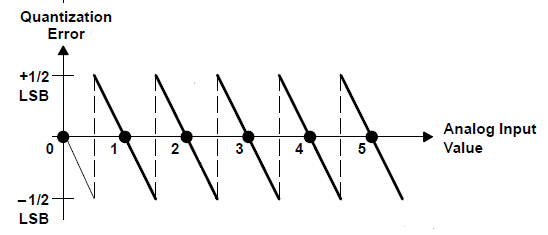
图 3：固有量化误差。

等式 6 计算一个步长上误差的平均噪声功率（均方），其中q 等于 1 LSB：

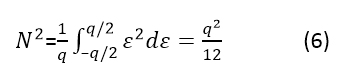
因此，公式 7 给出了 SNR 功率比：

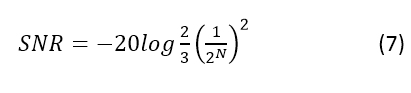
如果将量化噪声和整体噪声（复合 RMS DNL）与输入噪声一起包含在公式 5 中描述的抖动效应中，您将得到公式 8：

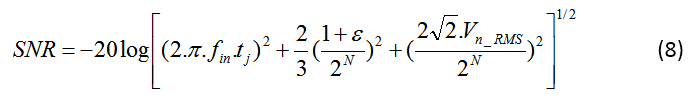
括号内的第一项是前面讨论过的抖动的影响。第二项是量化噪声和线性误差的影响，第三项是输入噪声的影响。

在抖动、量化噪声和输入噪声为零的理想情况下，您将得到以下众所周知的 SNR 公式（公式 9）：

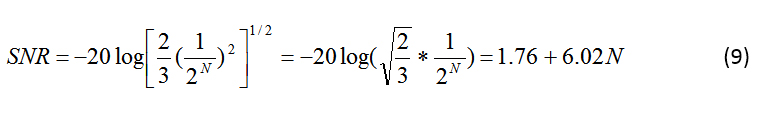
在实践中，通常使用公式 8 的前两项，而忽略第三项。您可以使用公式 8 从特定条件下测量的 SNR 计算抖动和量化误差。为了计算量化误差，应用了低 f in ，因此抖动的影响可以忽略不计，可以忽略不计。您可以使用得到的低频 SNR 的测量结果来计算公式 10 中的 ε ：

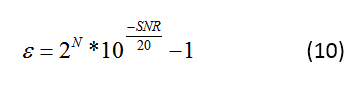
为了计算抖动，应用高频输入并再次测量 SNR。在这种情况下，抖动是导致 SNR 下降的主要因素。在f的高频处使用新的 SNR ，您可以 使用公式 11轻松计算t j ：

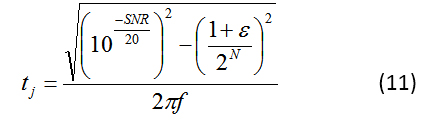
输入信号

如果输入不是满量程，它会相应地降低 SNR，这种影响很容易量化。例如，如果输入正弦波的幅度为 V in，是满量程的一小部分，则理想 SNR 将降低 20 log (2V in /V FS )。如果将幅度为 2V 的正弦波应用于 VFS 为 5V 的 12 位 ADC，则输入将使 74dB 的理论 SNR 降低 1.938dB，从而产生 72.062dB 的 SNR。

ADC 的另一个动态性能参数是信噪比和失真比（SINAD 或 SNRD）。SINAD 与 ENOB 的关联方式与 SNR 和 NOB 的关联方式相同。根据定义，您可以通过包括噪声和总谐波失真 (THD) 效应来计算 SINAD（公式 12）：

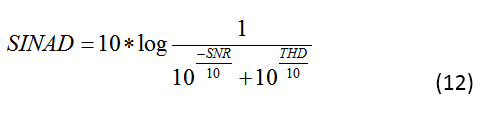
或者，您可以简单地使用等式 10 并将 SNR 替换为 SINAD，将 N 替换为 ENOB，从而以 ENOB 表示 SINAD。

过采样

到目前为止，我假设以奈奎斯特速率进行采样，这意味着采样率是被采样信号最大频率的两倍。现在，让我们研究过采样（超过奈奎斯特速率的采样）对 SNR 的影响。为此，采样频率 (fos) 与奈奎斯特频率之比 2 fo 就是过采样率 (OSR = f os /2f 0 )。

但首先，让我们看一下量化误差 ε，它在前面的方程中用于计算 SNR。ε具有位于±(Δ/2)之间的相等概率，其中D是LSB或简单地V FS /2 N。等式 13 将量化噪声功率表示为：

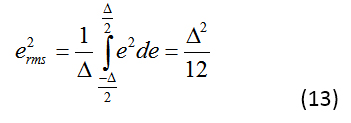
公式 14 给出了落入信号带宽（0 到 fo）的噪声功率：

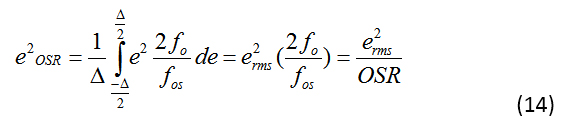
等式 14 说明了一个有趣的点：过采样降低了感兴趣频带中的量化噪声，从而提高了 SNR。事实上，您可以使用公式 15 量化 SNR 的改进：

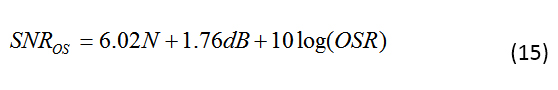
从公式 15 可以看出，SNR 每倍频程提高 3 dB。因此，如果 OSR = 2，则 SNR 提高 3 dB；如果 OSR = 4，则 SNR 提高 6 dB。

在图4中，采样频率每倍频程增加了3dB；因此，本底噪声下降了 9 dB，这相当于提高了相同数量的 SNR。

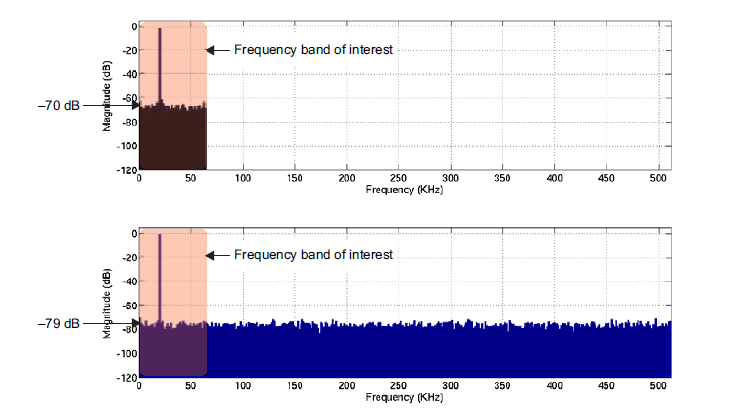
图 4：由于过采样而降低了本底噪声。

DNL

DNL 错误会降低整体 SNR。在某个频率以下，THD 仅取决于 ADC 的整体 INL；超出该频率，转换器的动态性能就会出现。

让我们制定1 LSB DNL的限制，这是不丢失代码的条件；这相当于分辨率降低 1 位，因此 SNR 降低 6 dB。对于线性误差为 1 LSB 的 n 位转换器，公式 16 将线性误差引起的 SNR 边界表示为：

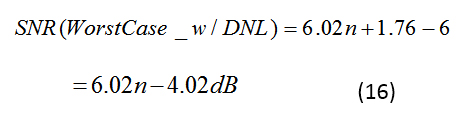
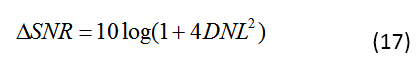
　　审核编辑：汤梓红