灰度共生矩阵(GLCM)基本原理

灰度共生矩阵

灰度共生矩阵(Gray Level CO-Occurrence Matrix-GLCM)是图像特征分析与提取的重要方法之一，在纹理分析、特征分类、图像质量评价灯方面都有很重要的应用，其基本原理图示如下：

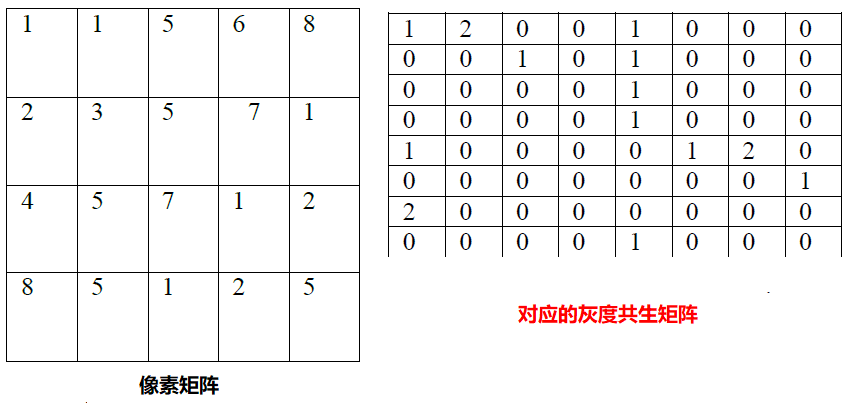
左侧是一个图像，可以看出最小的灰度级别是1，最大的灰度级别是8，共有8个灰度级别。右侧对应的灰度共生矩阵，左上角第一行与第一列的坐标(1, 1)包含值1，原因在于水平方向上，相距一个像素值，当前像素跟水平右侧相邻像素只有一个是1、1相邻的像素值(灰度级别)对；右侧共生矩阵的原始(1, 2) = 2 说明在像素矩阵中有两个像素值1，2相邻的像素点对、以此类推得到完整的右侧灰度共生矩阵。根据当前像素跟相邻像素位置不同，可以计算得到不同的共生矩阵，同时根据像素之间的距离不同会输出不同灰度共生矩阵。总结来说，有如下四种不同角度的灰度共生矩阵：

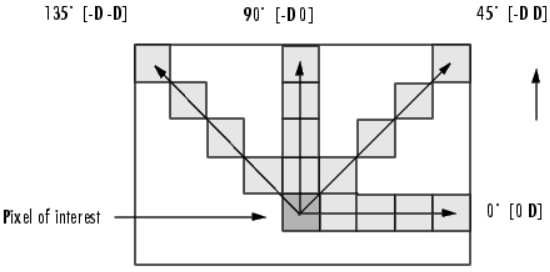
0度水平方向GLCM

45度方向GLCM

90度垂直方向GLCM

135度方向GLCM

根据相邻像素点之间距离参数D不同可以得到不同距离的GLCM。此外对正常的灰度图像来说，最小灰度值为0，最大的灰度值为255，共计256个灰度级别，所以GLCM的大小为256x256，但是我们可以对灰度级别进行降维操作，比如可以每8个灰度值表示一个level这样，这样原来256x256大小的共生矩阵就可以改成256/8 * 256 /8 = 32x32的共生矩阵。所以最终影响灰度共生矩阵生成有三个关键参数：

角度 (支持0、45、90、135)

距离（大于等于1个像素单位）

灰度级别(最大GLCM=256 x 56)

GLCM实现纹理特征计算

灰度共生矩阵支持如下纹理特征计算，它们是：

能量

熵值

对比度

相关性

逆分差

这些纹理特征计算公式如下：

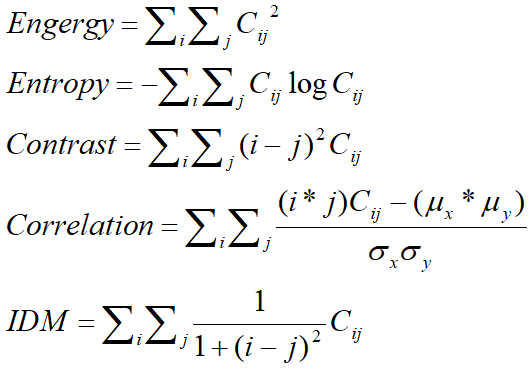
上述5个是常见的GLCM的纹理特征，GLCM总计由14个特征值输出，这里就不再赘述了！感兴趣的可以自己搜索关键字GLCM。

OpenCV计算灰度共生矩阵

OpenCV本身没有灰度共生矩阵的算法实现，所以需要对照自己编码实现，计算图像灰度共生矩阵，代码实现步骤如下：

加载图像，灰度转

创建灰度共生矩阵Mat对象

计算灰度共生矩阵

显示灰度共生矩阵

这里我采用的角度为0、45、90、135、像素距离d=1、灰度级别为256，代码实现如下：

 

// 0°， 45°， 90°， 135°
Mat glcm_0 = Mat::zeros(Size(step, step), CV_32FC1);
for (int row = 0; row < height; row++) {
    for (int col = 0; col < width; col++) {
        int i = gray.at(row, col);
        int j = gray.at(row, col + 1);
        glcm_0.at(i, j)++;
    }
}

Mat glcm_45 = Mat::zeros(Size(step, step), CV_32FC1);
for (int row = 1; row < height -1; row++) {
    for (int col = 1; col < width-1; col++) {
        int i = gray.at(row, col);
        int j = gray.at(row-1, col + 1);
        glcm_45.at(i, j)++;
    }
}
Mat glcm_90 = Mat::zeros(Size(step, step), CV_32FC1);
for (int row = 1; row < height-1; row++) {
    for (int col = 0; col < width; col++) {
        int i = gray.at(row, col);
        int j = gray.at(row-1, col);
        glcm_90.at(i, j)++;
    }
}
Mat glcm_135 = Mat::zeros(Size(step, step), CV_32FC1);
for (int row = 1; row < height; row++) {
    for (int col = 1; col < width; col++) {
        int i = gray.at(row, col);
        int j = gray.at(row-1, col - 1);
        glcm_135.at(i, j)++;
    }
}

normalize(glcm_0, glcm_0, 0, 1.0, NORM_MINMAX);
normalize(glcm_45, glcm_45, 0, 1.0, NORM_MINMAX);
normalize(glcm_90, glcm_90, 0, 1.0, NORM_MINMAX);
normalize(glcm_135, glcm_135, 0, 1.0, NORM_MINMAX);

 

运行效果如下：图一

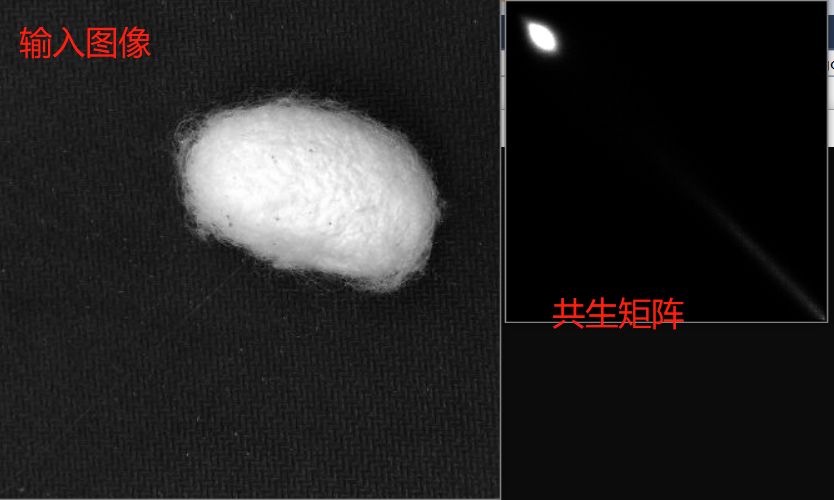
斑马线的灰度共生矩阵

提取图像对比度特征

基于共生矩阵实现纹理特征计算，这里我用了比较简单的对比度计算来实现局部纹理特征提取、代码实现如下(局部窗口大小8x8、灰度级别256/32 =8个级别)

 

int step = 256;
Mat image = imread("D:/images/ftexture.jpg");
// Mat image = imread("D:/images/ban_texture.jpg");
Mat gray;
cvtColor(image, gray, COLOR_BGR2GRAY);
imshow("gray", gray);
int height = gray.rows;
int width = gray.cols;

Mat glcm_0 = Mat::zeros(Size(width, height), CV_32FC1);
Rect roi;
roi.x = 0;
roi.y = 0;
roi.width = 8;
roi.height = 8;

for (int row = 4; row < height-4; row++) {
    for (int col = 4; col < width-4; col++) {
        roi.x = col-4;
        roi.y = row - 4;
        float pv = calculate_matrix(gray(roi));
        glcm_0.at(row, col) = pv;
    }
}
normalize(glcm_0, glcm_0, 0, 1.0, NORM_MINMAX);
imshow("glcm", glcm_0);
waitKey(0);

 

方法计算灰度矩阵的代码如下:

 

Mat m = Mat::zeros(Size(8, 8), CV_32FC1);
for (int row = 0; row < im.rows-1; row++) {
    for (int col = 0; col < im.cols-1; col++) {
        int i = im.at(row, col) / 32;
        int j = im.at(row+1, col+1) / 32;
        m.at(i, j)++;
    }
}
float contrast = 0;
for (int i = 0; i < 8; i++) {
    for (int j = 0; j < 8; j++) {
        contrast += m.at(i, j)*(i - j)*(i - j);
    }
}
return contrast;

 

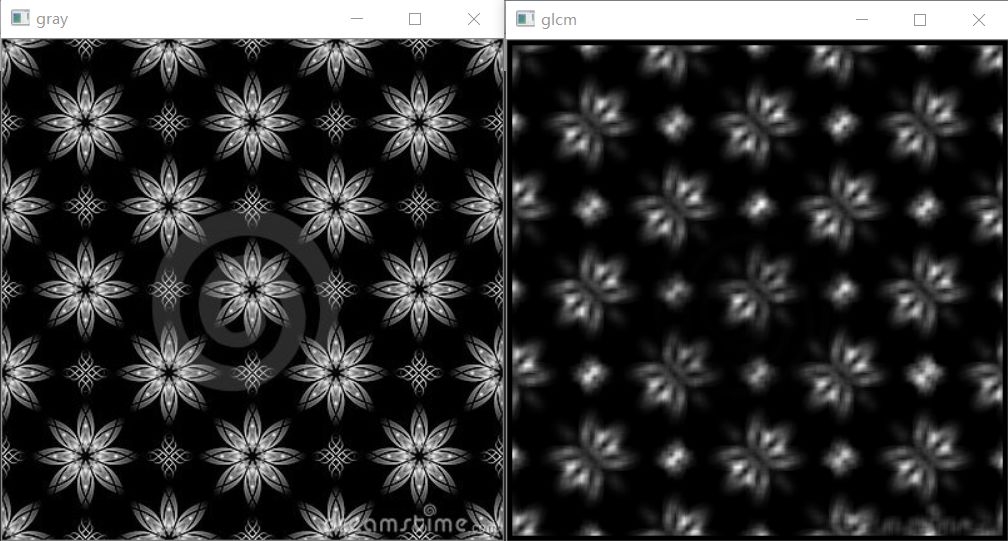
计算135°的灰度共生矩阵，基于计算局部对比度提取纹理运行结果如下：

测试一（左侧是输入图像、右侧135的对比度）

　　

      审核编辑：彭静