半导体激光器的准直原理

1.设计指标

快轴发散角：

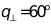
慢轴发散角：

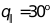
发光面尺寸：500

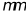
×0.2

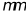
经发射系统后达到以下指标：

快轴发散角：0.5mrad(0.02°左右)

慢轴发散角：0.5mrad

2.其他参数确定

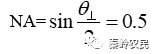
(以最大发散角定义)

准直后光束口径为d，则准直系统焦距为

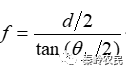
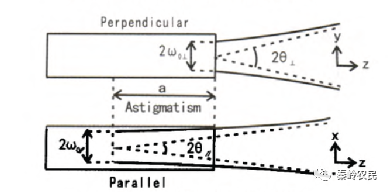
半导体激光器有源层很薄，在垂直于和平行于结平面的两个方向上发光面尺寸不同，Y方向远小于石方向的发光面尺寸，LD远场辐射图如图1所示。由矩孔衍射原理可知，半导体激光器的远场光强分布为z、Y两个方向上单缝衍射效应的叠加，沿z、Y方向中央亮斑的扩张与半导体激光器发光面长和宽的线度成反比变化。Y方向发光面尺寸较小，光的衍射效应较明显，衍射图样较宽，对应较大的发散角;x方向发光面尺寸较大，光的衍射效应不明显，衍射图样较窄，对应较小的发散角，即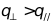。因而，LD输出光束为具有一定像散的椭圆高斯光束。

其中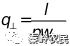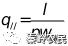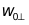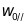，，。，为x，y方向的束腰半径。

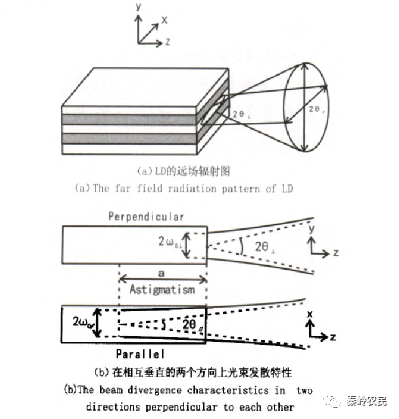
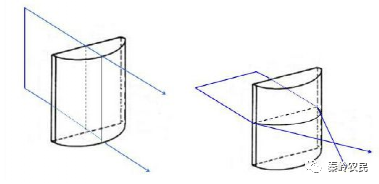
图 1 半导体激光器的发散光束性质

4.准直原理

如图1 所示，半导体激光器发出的子午光线先经过母线平行于激光束慢轴方向的柱透镜后变成准平行光束( 平行光束不可能实现) 。由于第2 个柱透镜M2对于子午光线的发散角无影响，可看作平板玻璃。图2 显示弧矢光线经过第1 个透镜M1时，光束会发生偏移，但不会影响光束的发散角，在经过第2 个柱透镜时，弧矢光也同样得到准直，输出准平行光。

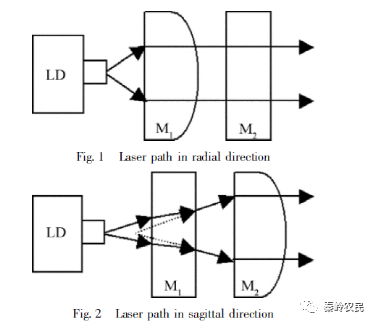
FAC: fast axis collimation

SAC: slow axis collimation

5.光源设置

渐晕系数VCX=1-tan(15°)/ tan(30°)=0.5359

6.模型建立

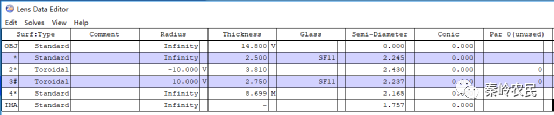
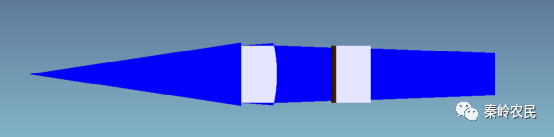
以newport公司的SAC和CL透镜为准直元件，在zemax中序列模式中建立模型。由于透镜曲率不知，未优化时，此模型并不能起到将光斑压缩成圆斑的效果，需进一步优化。

7.序列模式模拟激光二极管光源——光线模型

7.1不考虑Astigmatism的模拟方法

没有像散特性时，假设激光二极管是点光源，带有高斯的强度分布，以及指定散角的椭圆分布。物距设置为100mm。如下图：

输入发散角较大的方向的NA值。

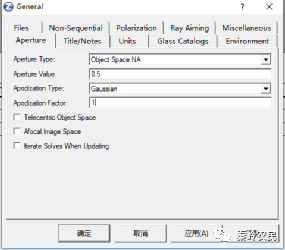
下面将光束改为椭圆。计算光束投影到入瞳平面上时，半径的比值。

渐晕系数VCX=1-tan(15°)/ tan(30°)=0.5359，即可产生一个0.5359：1的椭圆型光束。软件中设置如下：

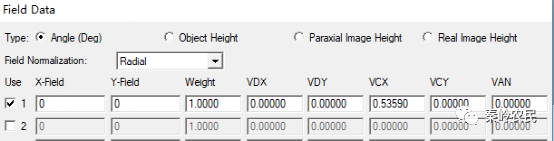
效果如下：

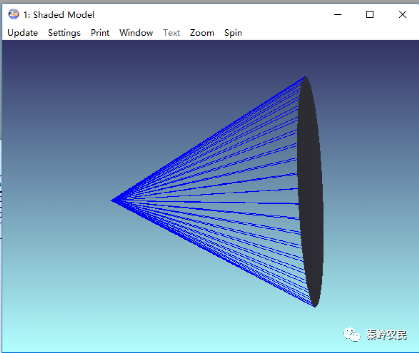
查看距离光源100mm位置的照度：

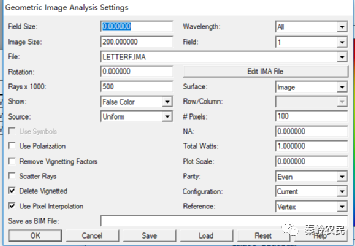
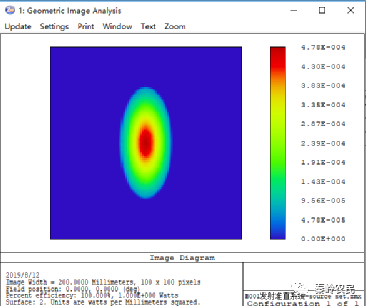
查看距离光源Y截面分布。

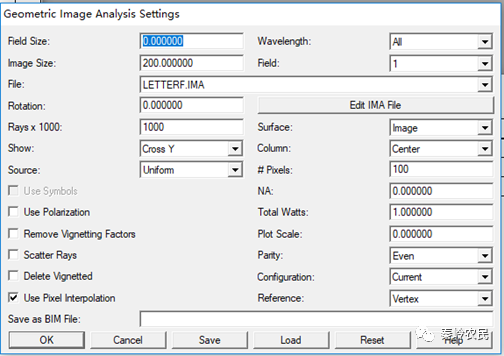
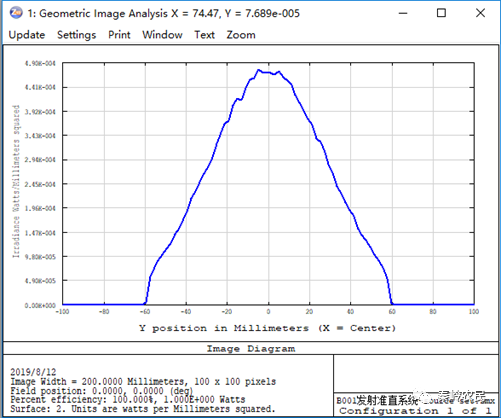
可以看到，大约在100×tan(30°)=57.7mm处，其强度降到了1/e2。

查看距离光源X截面分布。

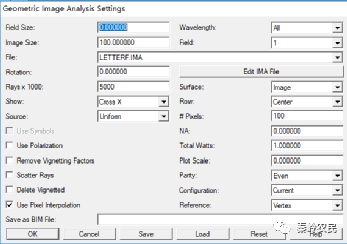
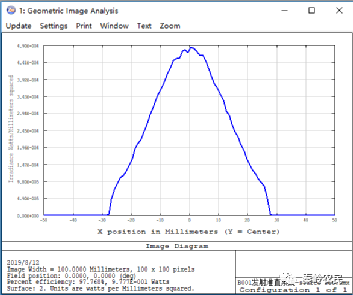
可以看到，大约在100×tan(15°)=26.79mm处，其强度降到了1/e2。

7.2带有Astigmatism的模拟方法

一般来说，激光器厂商提供的规格表中不一定提供Astigmatism值，因此通常把激光二极管作为点光源模拟。但如果在实验室中通过适当的方法，可能测出Astigmatism的值。

如果在非序列模式下，带有Astigmatism的椭圆形高斯光束可以用Source Diode光源物件来模拟，而在序列模式中，则可以利用理想圆柱透镜(Paraxial XY)的设置，加上点光源来完成。由于Astigmatism的特性即是X与Y方向的焦点位置不同，因此我们可以利用单方向的理想圆柱透镜，透过成像公式计算，改变光束在某一方向上的焦点位置，下面是我们要设定的系统，我们会透过Paraxial XY这个Surface改变光束在Y方向上的发散角及焦点位置。

虚光腰距出光端面的距离(即像散)，可由下式确定：

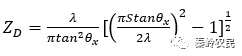
(5.1)

式中，各参数的定义为

λ—波长

S—有源层宽度

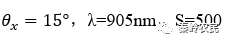
微米。计算得：

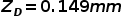
设定方法如下：

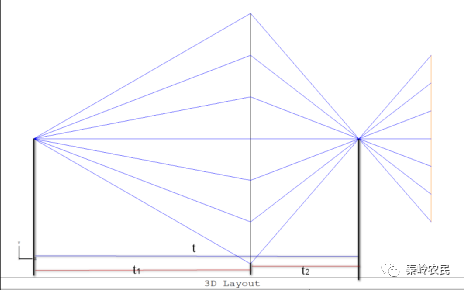
1.光源在x方向半发散角

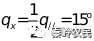
，光源在y方向半发散角

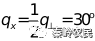
，Astigmatism=t

2.使用下面公式计算M(放大率)

(理想柱透镜的屈光能力)：

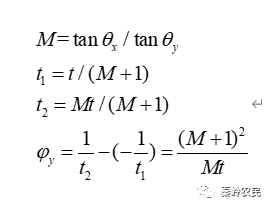
1

3.输入NA=sin(θx)=0.26

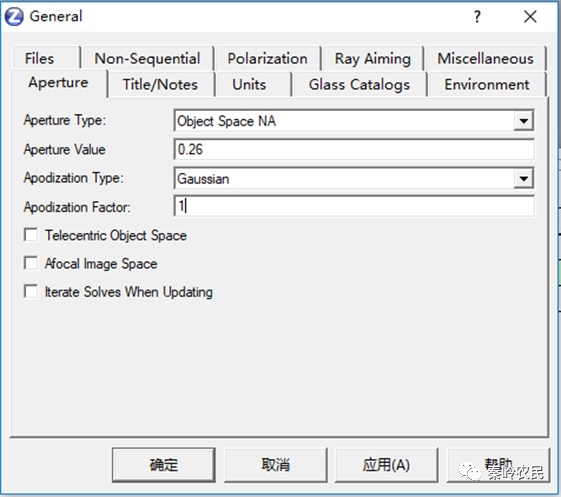
4.物面到第一面的距离设置为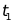

5.第一面设置为光阑面，并设定面型为Paraxial XY：X power=0;Y power=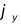

6.带有Astigmatism的光源就设定好了。此光源在X方向的焦点在第0面，而Y方向的焦点在第一面开始往后位置上。

对于窄线宽激光器，暂定参数为：

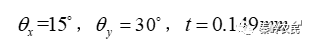
依据公式组1，计算得：

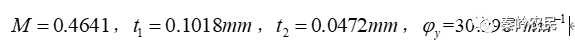
查看焦点位置的照度：

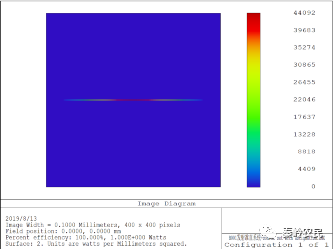
查看距离光源0.1mm位置的照度：

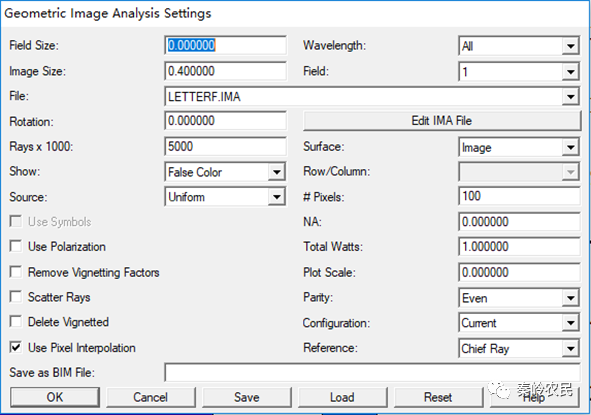
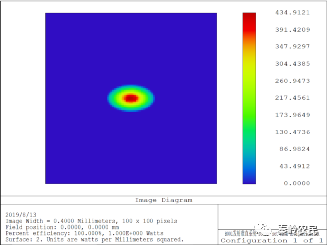
查看距离光源0.2mm位置的照度：

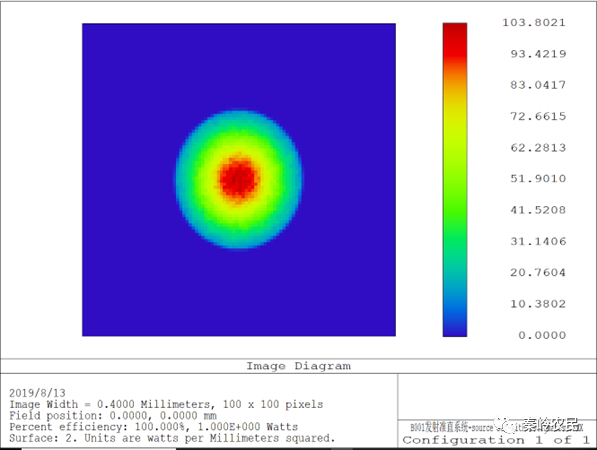
查看距离光源0.3mm位置的照度：

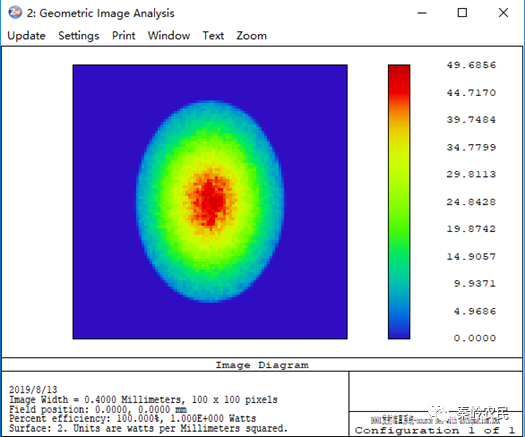
查看距离光源1mm位置的照度：

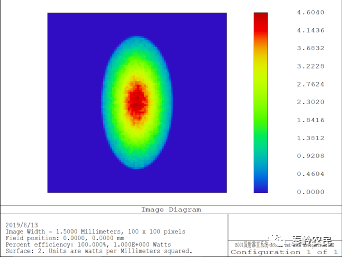
查看X与Y Cross，结果如下：

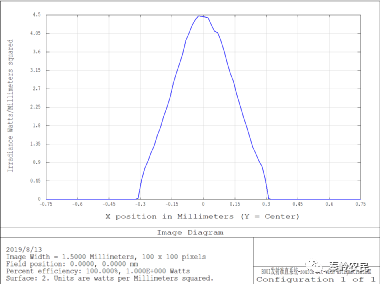
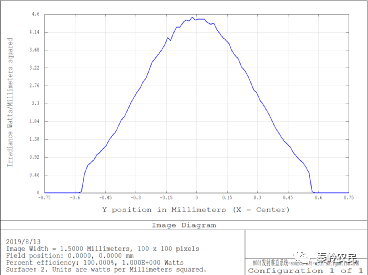
可以看到，X方向的1/e2强度约落在0.26左右，与发散角正切值tan(15°)=0.268吻合;

Y方向的1/e2强度约落在0.57左右，与发散角正切值tan(30°)=0.577吻合。

审核编辑：汤梓红