关于相对论里因果律的问题

 

在牛顿力学里，时间是绝对的，所有参考系都共用同一个时间。因此，只要在某个参考系里事件A先于事件B发生，那必然在所有的参考系里事件A都先于事件B。

比如，我们在某个参考系里观察到一个人先出生，后去世。那么，不管你在哪个参考系里观察，都会看到这个人先出生，后去世。因为牛顿力学里只有一个时间，因此这个非常自然的，因果律也不会出现什么问题。

但是，到了狭义相对论这里，事情就有点不一样了。

我们都知道，狭义相对论里时间是相对的。在一个参考系里同时发生的两个事件，在另一个参考系就可能是不同时的，这就是同时的相对性。同时的相对性是爱因斯坦创立狭义相对论的关键。

既然在狭义相对论里同时性是相对的，时间也是相对的，那我们就有一个疑问了：既然时间是相对的，那么在一个参考系里具有因果关系的两个事件（比如一个人先出生，后去世），是否有可能在另一个参考系里因果颠倒了呢（变成先去世，后出生）？

 

这就是狭义相对论里的时序和因果问题。

1

为了让大家更直观地理解这个事，我们来看一个更简单的例子：我们在地面系K看到一把手枪沿着x轴正方向发射了一发子弹，击碎了一个花瓶。我们把子弹发射的事件记为p1，击碎花瓶的事件记为p2。

在地面系，我们记录了子弹发射的时间为t1，在x轴的坐标为x1。也就是说子弹发射事件可以记为p1（t1，x1），同样，击碎花瓶的事件可以记为p2（t2，x2）。

因为我们在地面系K观察到的是子弹先发射，后击碎花瓶，那么，在地面系自然就有t2》t1。现在我们变换参考系，假设在一个新的惯性系K‘里，将子弹发射的发射事件p1记为（t1’，x1‘），击碎花瓶事件p2记为（t2’，x2‘）。

如果在惯性系K’里，我们依然看到先发射子弹，后击碎花瓶，也就是有t2‘》t1’，那么事件发生的时序就没有改变，因果律也不受影响。但是，如果你一旦发现在K‘系里出现了t2’《t1‘，那就表示在这个新的惯性系里击碎花瓶的事件先于子弹发射事件发生，那时序就更改了，因果律就会受到严重的威胁。

那么，我们要如何讨论惯性系K’里时间t1‘和t2’的关系呢？答案，当然是根据洛伦兹变换。

在狭义相对论里，联系两个惯性系之间时空变换关系的就是洛伦兹变换：

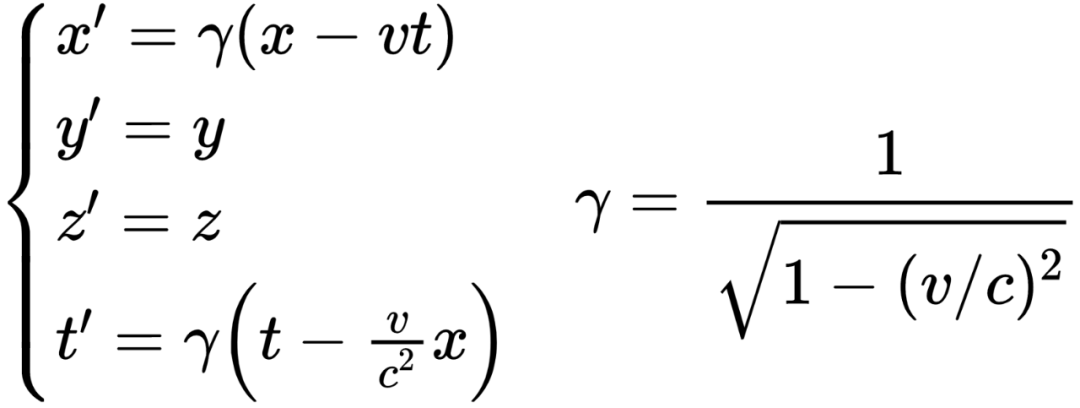
也就是说，如果一个事件在地面系K的发生时间为t，那么，在相对地面以速度v向右运动的惯性系K‘里，这个事件的发生时间就变成了上面的t’。

如果我们再取几何单位制，也就是取光速c=1，那么时间t‘的表达式就可以简化为：t‘=γ（t-vx）。

很显然，假设地面系事件p1和p2发生的时间差表示为Δt（Δt=t2-t1），那么，根据上面的式子，惯性系K’里这两个事件的时间差Δt’=γ（Δt-vΔx）（这里Δt‘=t2’-t1‘）。

这就是说，如果Δt‘》0，那么在惯性系K’里依然是p2在p1之后发生，时序并未发生变化，不存在因果律问题；如果Δt‘《0，那就是说惯性系K’里p2（击碎花瓶）先于p1（子弹发射）发生，时序发生了改变，因果律面临挑战。

那么，Δt‘=γ（Δt-vΔx）是大于0还是小于0，我们要怎么看呢？

2

在狭义相对论里，同一个事件在不同的惯性系里可以有不同的时间坐标和空间坐标，两个事件之间的时间间隔和空间间隔都是相对的。但是，它们组成在一起的时空间隔确是绝对的，是不随任何参考系的改变而改变的，这是狭义相对论的核心，甚至可以说是狭义相对论的全部内容（这个结论通过洛伦兹变换可以很容易证明出来，这里不细说）。

也就是说，在地面系K和惯性系K’里，事件p1=（t1，x1）=（t1‘，x1’）和事件p2=（t2，x2）=（t2‘，x2’）的时间间隔可能并不相同（Δt≠Δt‘），空间间隔也并不相同（Δx≠Δx’）。

但是，它们的时空间隔肯定是相等的，即：-Δt²+Δx²=-Δt’²+Δx‘²（时空间隔的定义为I=-Δt²+Δx²）。

因为两个事件的时空间隔是绝对的，在任何参考系里都是相同的。因此，我们可以用两个事件的时空间隔这个绝对量作为标准，来讨论不同惯性系里事件的时序，这样讨论出来的结果就对任何参考系都有效。

接下来，我就给出下面这个极为重要的结论：如果两个事件之间的时空间隔小于0，也就是I=-Δt²+Δx²《0（我们称这个间隔是类时的），那么，任何洛伦兹变换都不会改变时序；如果两个事件之间的时空间隔大于0，也就是I=-Δt²+Δx²》0（我们称这个间隔是类空的），那么，则必有改变时序的洛伦兹变换。

这个结论其实很容易证明，你想，如果两个事件的时空间隔是类时的，也就是I=-Δt²+Δx²《0。那么，自然就有Δx²《Δt²，因为Δt是地面系两个事件的时间间隔，我们约定Δt》0，那么就有|Δx|《Δt。

而我们这里采用的是几何单位制，光速c=1，而我们也知道狭义相对论里所有物体的速度都是小于光速的，两个惯性系之间的相对速度v《1。于是，很自然就有Δt》|Δx|》v|Δx|。

由于Δt》v|Δx|，那么Δt‘=γ（Δt-vΔx）》0。也就是说，在地面系K里有Δt》0，在惯性系K’里，依然有Δt’》0。这样，时序就没有发生改变，在一个惯性系K里先发生事件p1后发生p2（Δt》0），在另一个惯性系K‘里依然是先发生事件p1后发生事件p2（Δt’》0），因果律依然得以维持。

同样，你可以类似的证明，如果两个事件之间的间隔是类空的，也就是I=-Δt²+Δx²》0，那必然有改变时序的洛伦兹变换。

3

这结论到底告诉我们什么呢？如果两个事件之间的时空间隔是类时的，那么，无论你怎么构造洛伦兹变换更改参考系，都不会影响这两个事件的时序。在一个参考系里是事件A先事件B后，那么在所有的参考系里就都是事件A先事件B后，这样当然就不存在因果律困难。

那么，两个事件之间的时空间隔是类时的是什么意思？简单来说，如果我们画一个二维的时空图，横轴代表空间x，纵轴代表时间t，那么时空图里斜率的倒数就代表速度。

因为我们采用的是几何单位制（c=1），因此45°的那条直线的斜率为1，也就是说如果有一个粒子的运动轨迹是45°线，那么它就是以光速运动的。而一般有质量的粒子，速度小于光速c，那么在时空图里的斜率就会大于1（这样斜率的倒数-速度才会小于1，也就是小于光速了，如L2）。

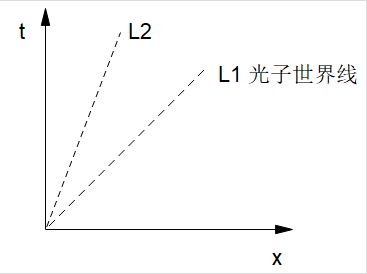
而时空间隔的定义，我们前面也说了：I=-Δt²+Δx²。如果两个事件之间的时空间隔小于0，我们就说这个时空间隔是类时的。你可以看到，如果让时空间隔I《0，就需要想粒子在x轴方向的变化Δx小于在时间t上的变化Δt，也就是它们的连线是偏向时间轴t，就像L2那样。

这样，等于说我们就知道了：如果两个事件之间的时空间隔是类时的，任何洛伦兹变换都不会改变时序。而且，任何一个有质量的粒子在时空图上走的轨迹（叫粒子的世界线），任何两点之间的时空间隔也是类时的，否则这个粒子就要超光速了。

把它们连起来，那么任何真实粒子自己世界线上的事件，在狭义相对论里，在洛伦兹变换下都不会改变时序，都不会出现因果律问题（我们上面的只证明了沿x轴方向洛伦兹变换有这个特性，其实一样可以证明任意方向的洛伦兹变换都有一样的结论）。

也就是说，比如我们地面系看到子弹一开始在手枪这里，过了一段时间之后跑到了花瓶这里。那么，子弹发出事件和击碎花瓶事件就都是子弹世界线上的两个事件，这样两个事件之间的时空间隔必然是类时的，因此不论在哪个参考系里看，你都只能看到子弹先发出，后击碎花瓶，不会违反因果律。

4

如果两个事件之间的时空间隔是类空的，也就是两点的连线会偏向空间坐标x这边，那么就必然会出现改变时序的洛伦兹变换（这个结论的后一半）。也就是说，必然会在某个惯性系看到这两个事件的时序不一样，会先后颠倒。

但是，因为两个类空的事件不可能是一个粒子的世界线，它们之间本来就没有因果关系。什么叫因果？事件A发生了一个信号，这个信号影响出现了事件B，这样我们才能说它们之间有因果关系。因为相对论里信号传递的速度有一个上限，也就是光速，因此两个有因果联系的事件之间，最大也就通过光速联系。

而两个有类空间隔的事件，如果它们之间有信号联系，那必然超光速，这是相对论里不允许的。因此，两个类空事件之间必然没有因果联系，所以，它们在不同的参考系里时序不一样也没有什么大惊小怪的。

基本上，你只要看到谁谁谁说他从狭义相对论的时间、空间的相对性出发，发现了有什么事情违反了因果律。那么，要么是他想错了，要么就是这两个事件之间的时空间隔是类空的，二者本来就没有因果联系。

比如，我们在地面系看到张三家的鸡下了一个蛋，然后0.1秒以后，在30万公里以外的李四家的狗叫了一声。这样两个事件，完全可以在另一个参考系里看到是李四家的狗先叫的，张三家的鸡后下的蛋，但是这不会破坏因果律，因为这两个事件之间的时空间隔是类空的，它们本来就没有因果联系。

当然，你可以让这两个事件之间变得有因果联系。比如，张三家的鸡下了蛋以后，我们立马用光信号通知李四，让他家的狗叫一声。但这样的话，30万公里你至少需要1秒钟（光速c≈30万公里/秒），是不可能在0.1秒内完成的。

因为时空间隔是绝对的，两个事件只要在某一个惯性系里的时空间隔是小于0的，是类时的，那么在所有的惯性系里就都是类时的。所以，如果你想再寻找一个参考系，让在另外一个参考系里两个事件变得“光速可及”，也就是让它们的时空间隔变成类时的，就趁早死心吧~

虽然我们上面讨论的结论只是在二维洛伦兹变换（只沿着x轴）下得到的，但其实在任意洛伦兹变换下结论都成立，这个我就不再证明了。

最后，虽然我们上面讨论两个事件的时空间隔时，只讨论了类时的（I《0）和类空的（I》0）两种。但是，显然还有一种I=0的情况，这种时空间隔叫类光的。从时空图可以轻易看出，如果I=0，必然导致Δx=Δt，那么速度v=Δx/Δt=1，也就是光速。

也就是说，如果两个事件的时空间隔是类光的（I=0），而且这还是某个粒子的世界线，那就只能是光子或者其它光速运动的粒子。不难想象，它们也不会改变因果，是一个擦边的情况。

这样，大家明白狭义相对论里因果律的问题了么？　　

      审核编辑：彭静