

介绍一种实际的调谐质量阻尼器的设计准则
描述
在实际的工程应用中,工程结构往往并不是单自由度系统。不仅如此,阻尼器自身也有极大的可能并不是单自由度系统,下面我们就用一个工程案例来进行分析。
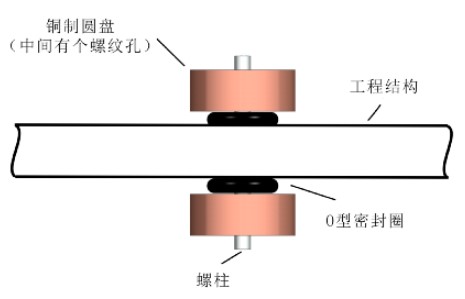
一个很简单的调谐质量阻尼器可以如上图所述。该减振器使用两个相同的铜质圆盘和弹性O型环,机械地连接到工程结构上。在这些圆盘的中间有两个螺纹孔,通过螺柱,这两个铜质圆盘被夹在主结构上。该螺柱穿过工程结构而不接触该结构。O型环的静态压缩可以通过螺纹杆进行调整。使用这个阻尼器的结构,在调整O型密封圈静态形变的同时,将接触面的摩擦降到最低。与此同时,在这种设计中,O型圈不仅为系统提供了刚度和阻尼,而且它们还隔离了作为TMD质量一部分的螺纹杆。因此,在设计中没有多余的部件,可以有效地节省成本以及提高可靠性。此外,这个阻尼器的刚度是可调的。随着不同的O型圈的静态压缩,可以获得不同的阻尼器的动刚度。不仅如此,这个阻尼器的刚度和阻尼也是可以预测的。因此,设计者就能够遵循一种非常简单的方法来设计这个阻尼器,即:
根据所需的TMD质量来选择螺纹杆和圆盘的材料和质量。
选择O型环的材料、直径和线径,以达到理想的阻尼和刚度。
静态压缩的最终调整,以达到最优化的共振频率。
1、调谐质量阻尼器的工作模态
在经典的调谐质量阻尼器的设计理论之中,往往只考虑其一个自由度。但对于实际的结构,它的工作模态通常更加复杂。对于我们所说的例子,这个阻尼器可以有压缩(compressive)、摇晃(rocking)和剪切(shear)等不同的工作模态。典型的模态形状在下图显示:
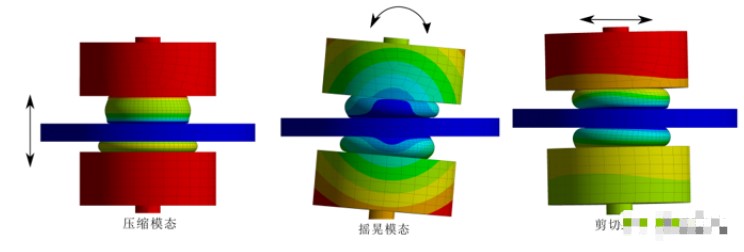
在这个阻尼器中,一般考虑的设计是压缩模态,因为其他模态可能会对主机结构产生意想不到的影响。它可能对于主体结构产生意外,造成有利或者有害的影响。例如,工程结构的横向振动将激发另外两个阻尼器模态(摇摆和剪切),它们会与工程结构的运动产生相互作用。这与理想的阻尼器设计原理是截然不同的。然而,这些额外的模态也可以提供有益的减振效果。判断这些额外的模态是否有效主要还是取决于工程结构的模态。
传统的调谐质量阻尼器一个重要的弊端是它只能在有限的频率范围内工作。对于这个实际的调谐质量阻尼器,每一个不同的模态将会对应一个不同的频率。这直接导致了这个阻尼器的可用工作频率变得更大。不仅如此,当我们压缩O型圈,从而改变这个弹性元件的静态压缩量时,O型圈的刚度可以变化,通过这个操作,这个阻尼器的固有频率也可以改变。在O型圈不同的静态压缩量时,这个阻尼器的固有频率可以如下图所示。

我们可以看到,随着静态压缩量的增加,这种阻尼器的共振频率将会大大提高。随着O型圈的静态压缩量的增加,它的刚度对于不同方向的几何非线性造成了不同的固有频率的增加量。摇摆模态对初始压缩的敏感度较高,这是因为在这种模式中,密封圈的变形不仅增加了其与金属表面的接触面积,还使O型圈进一步远离阻尼器的中心线,从而增加其对摇摆的阻力。对于其他模式,O型圈相对于阻尼器中心线的位置并不重要。因此,对于摇摆模态,我们可以观察到更大的刚性增强。
2、O型圈的刚度和阻尼变化曲线
在这个设计之中,O型圈是被作为阻尼器的刚度和阻尼元件。为了建立阻尼器的设计曲线(master curve),O型圈的刚度和阻尼的理论或者有限元模型需要被建立,然而,这里面包含相对比较复杂的数学模型。这里,我们只是将对O型圈与静态压缩量相关的阻尼和刚度变化的实验结果显示了出来:
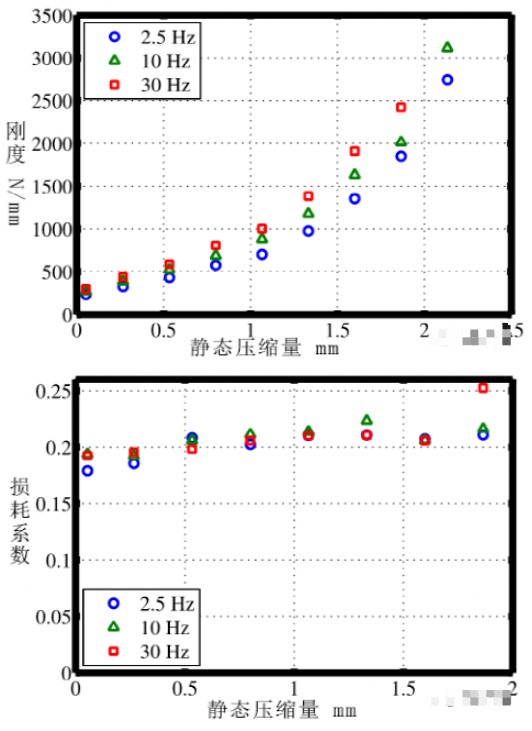
我们可以看到,O型圈的刚度随着静态压缩量呈多项式函数增长,而阻尼基本保持一致。这就为我们设计作用于宽频的调谐质量阻尼器提供了基础。
3、调谐质量阻尼器设计曲线
我们所设计的这个调谐质量阻尼器在选定的频率范围内,实质上有两个工作模态,阻尼器的拉伸压缩模态与摇摆模态。在设计时,我们在考虑最优化的设计参数时,也需要同时考虑这两个模态。在初始设计时,可以只考虑拉升压缩模态,用于选定阻尼器的质量参数。在选定阻尼器的质量时,以下几个原则必须考虑到:
阻尼器中质量块在竖直方向的局部模态(local mode)将不会影响到整个阻尼器的工作模态。
利用简单的螺柱连接,阻尼器的质量块需要对于O型圈施加均一的静态应变。
考虑到O型圈的刚度范围相对固定,阻尼器的质量块选择需要满足其设计频率。
下图中就显示了一个典型的调谐质量阻尼器设计曲线,它总和O型圈的静态压缩量有关。图中蓝色的实线代表阻尼器在拉伸压缩模态时的工作频率,绿色的虚线代表了其在摇摆模态时的工作频率。横向虚线代表了主结构的第一阶和第二阶的弯曲模态。纵向的点划线代表着若干选定的O型圈静态压缩量。
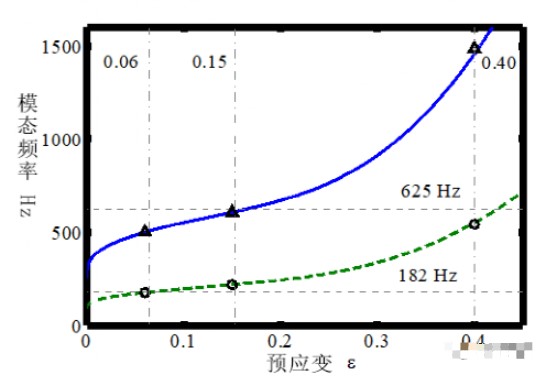
传统的阻尼器设计理论总是认为质量比对于阻尼器的调制频率有很大的影响。但实际上,这些阻尼器的设计理论往往都在考虑数学上的最优化解。在工程实践上,一个更为简化的方法就是假设阻尼器的工作模态频率和主结构的自然频率相等。这其实包含了以下几个假设:(1)阻尼器的质量通常远小于主结构的质量,它对于主结构的模态影响基本可以忽略不计;(2)对于调谐质量阻尼器,由于阻尼的存在,其对于阻尼器的模态频率敏感度有限。所以,为了便于设计,我们将阻尼器设计的模态频率假设为主结构的固有频率。
在上图中,我们可以看到当静态压缩量约为O型圈直径的6%、15%和40%时,结构和阻尼器之间会发生相互作用。对于一个小型O型圈而言,最小静态压缩量为其直径的6%左右。当静态压缩量小于6% 时,橡胶与金属的静摩擦力不足以使O型圈保持在其设计的位置。在这个压缩量时,阻尼器摇摆模态将作用于主结构的第一阶弯曲模态。当预压缩量增加到15%时,摇摆模态仍将对于第一阶弯曲模态有效,与此同时,拉伸压缩模态也将作用于第二阶弯曲模态。在O型圈40%的静态压缩量下,阻尼器摇摆模态则将减低主结构的第二阶弯曲模态的振动。
4、实验验证
实验验证的模型如下图所示。这个可调调谐质量阻尼器被安装在一个空心梁上。阻尼器被安装在梁的第二阶弯曲模态的反节点位置上(anti-node)。值得注意的是,两个激光传感器是用于判断O型圈的静态压缩量。
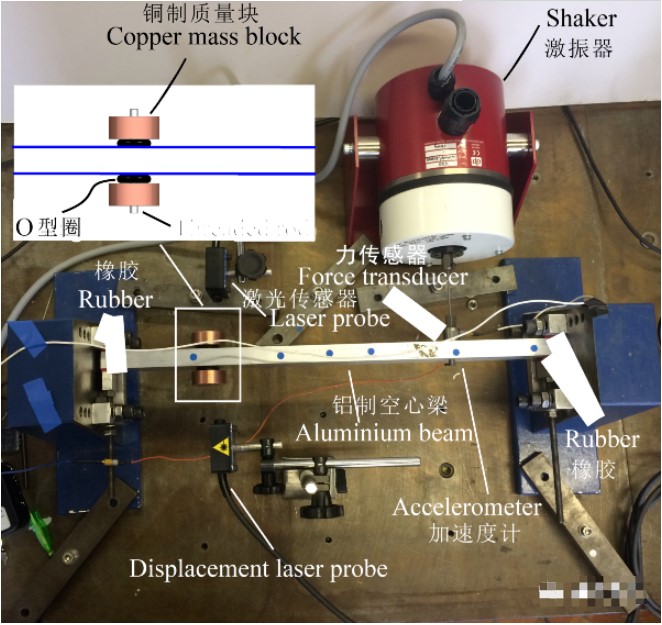
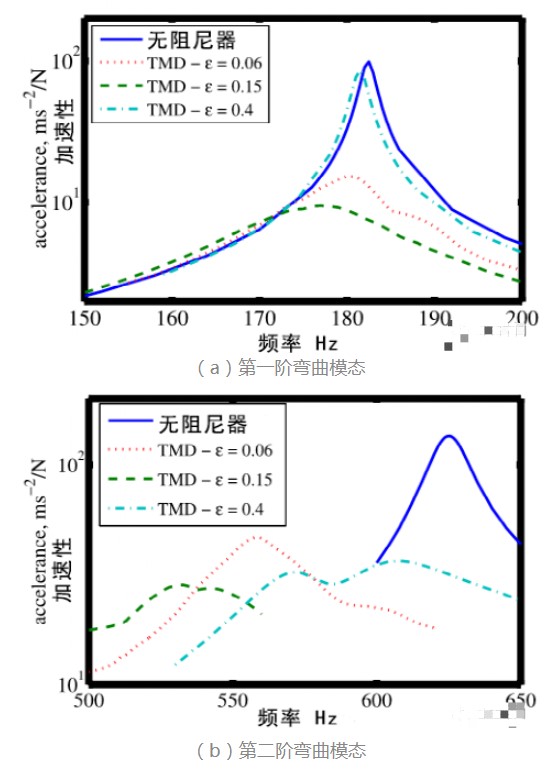
当阻尼器调整至不同的工作状态时,下面两张图片显示了空心梁上的加速度频响函数(accelerometer frequency response)。当O型圈受到6%的静态压缩率时,空心梁对于第一阶弯曲模态(约185Hz)的横向振动被抑制了10倍。随着静态压缩量的增加,阻尼器对于第一阶弯曲模态的结构震动控制变得不那么有效。当静态压缩率为40%时,600Hz附近的振动水平(与主结构的第二阶弯曲模态相关)几乎降低了8倍。最后,在O型圈15%的静态压缩率下,这两个结构共振都得到了有效的抑制。这些结果证实我们所使用的设计方法的可靠性。
5、结语
在这篇文章中,我们介绍了一种实际的调谐质量阻尼器的设计准则。它的设计方法源于基本的阻尼器理论。但是在实践中,我们需要考虑更多的变量,以便于我们的阻尼器更有效地工作在我们所需要的主结构模态。
审核编辑:刘清
-
阻尼器的工作原理与结构2025-02-13 5985
-
什么是液压阻尼器 阻尼器的常见故障及解决方法2024-12-06 4114
-
如何选择合适的阻尼器型号2024-11-14 2938
-
阻尼器是什么东西做成的 阻尼器和减震器一样吗2024-02-21 6828
-
什么是阻尼器 阻尼器是干什么用的 阻尼器和弹簧的区别2024-02-19 16790
-
阻尼器的原理和作用 阻尼器的种类及优缺点2024-02-18 27283
-
阻尼器的原理和作用 阻尼器怎么调节松紧2024-01-19 14489
-
磁流变阻尼器的3种工作模式2023-10-19 504
-
主要介绍调谐质量阻尼器的设计准则2022-08-16 7313
-
阻尼器是什么_阻尼器分类2019-11-07 20889
-
阻尼器工作原理2018-12-16 153312
全部0条评论

快来发表一下你的评论吧 !

