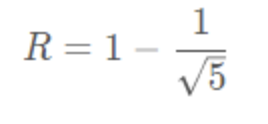电路分析中的ZT和DFT

简 介：这学期的信号与系统进展到第五章，拉普拉斯变换与 z 变换。前几天看到一篇博文中对于无限电阻网络求解相邻节点阻抗中使用了离散傅里叶变换 (DFT) 的方法比较新颖。分析了DFT在其中仅仅是起到描述线性时不变离散时间系统的作用，所以将其替换成 z 变换进行描述，则在分析求解过程中会更加的清晰。
关键词：z变换，DFT，电阻网络

01电阻网络

一、问题来源

在网文  Infinite Ladder of 1Ω of Resistor[1] 中讨论了如下无穷电阻网络两个相邻节点之间的电阻。特别有意思的是，文中还是用了离散傅里叶变换（DFT）给出了另外一种求解方式。这不禁让人们好奇：在这样的电阻网络分析中，离散傅里叶变换到底起到什么作用？

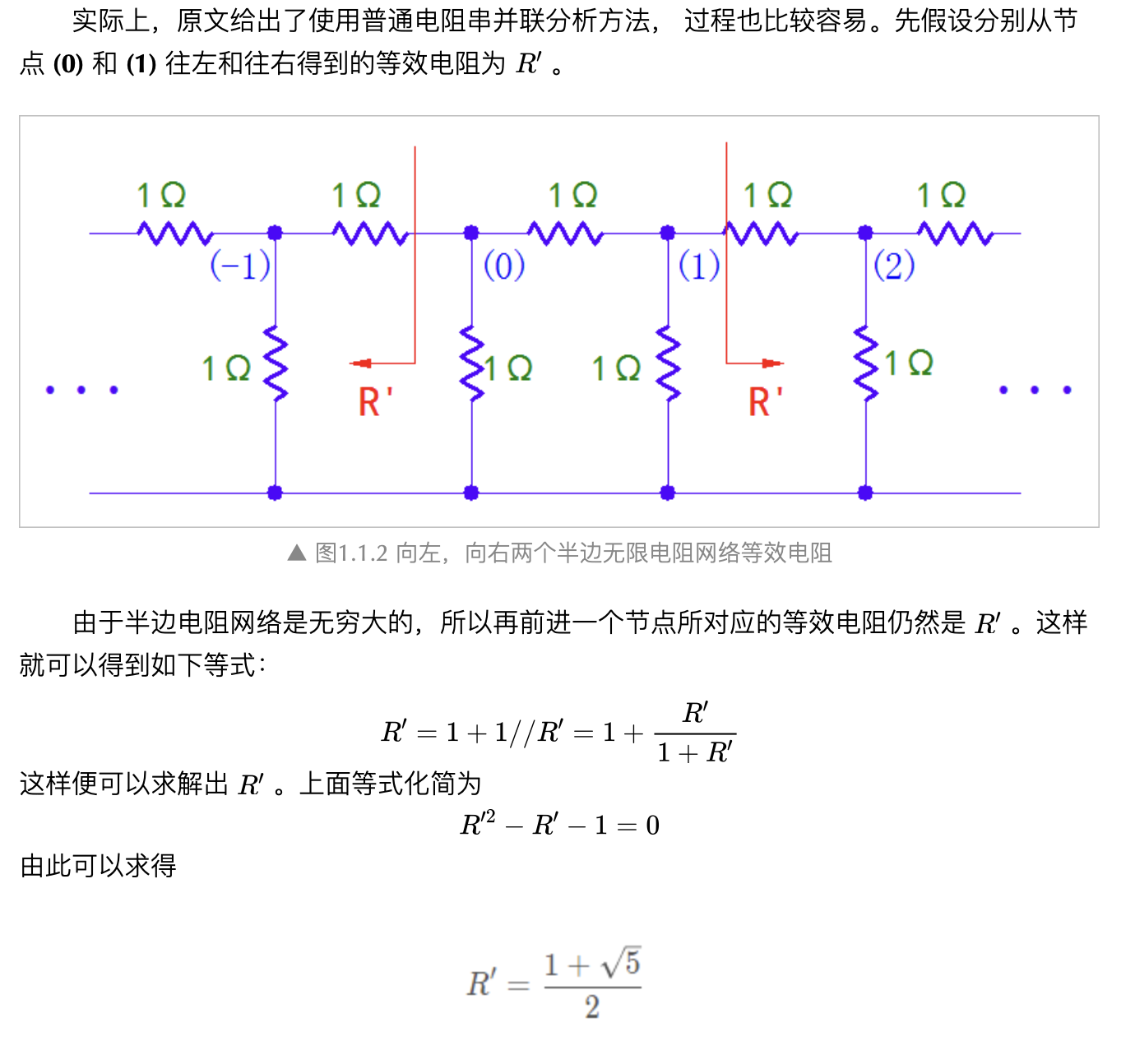
▲ 图1.1 一欧姆组成的无线电阻网络

二、问题求解

1、普通求解方法

 

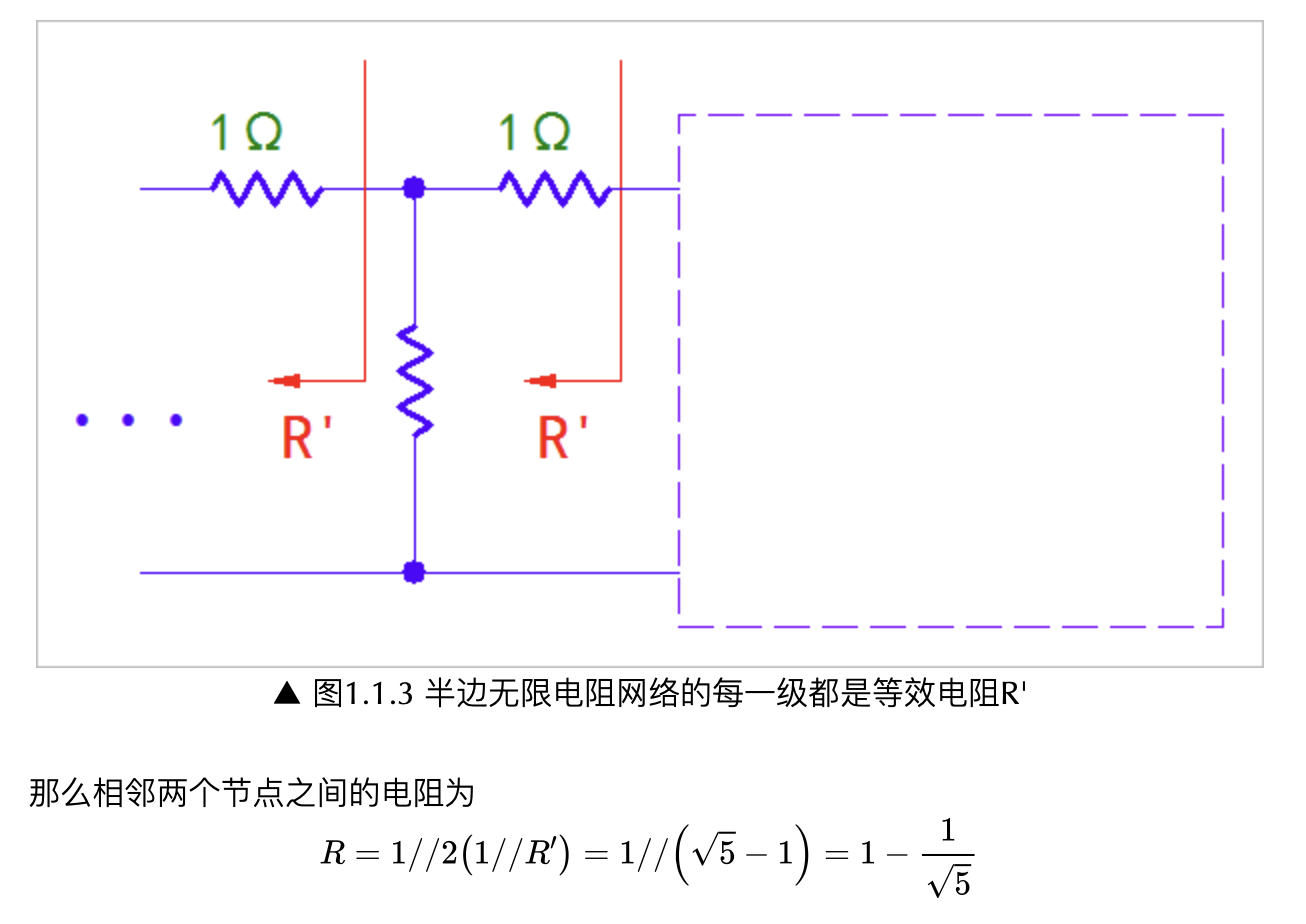
▲ 图1.1.4 相邻节点之间的等效电阻

2、离散傅里叶求解

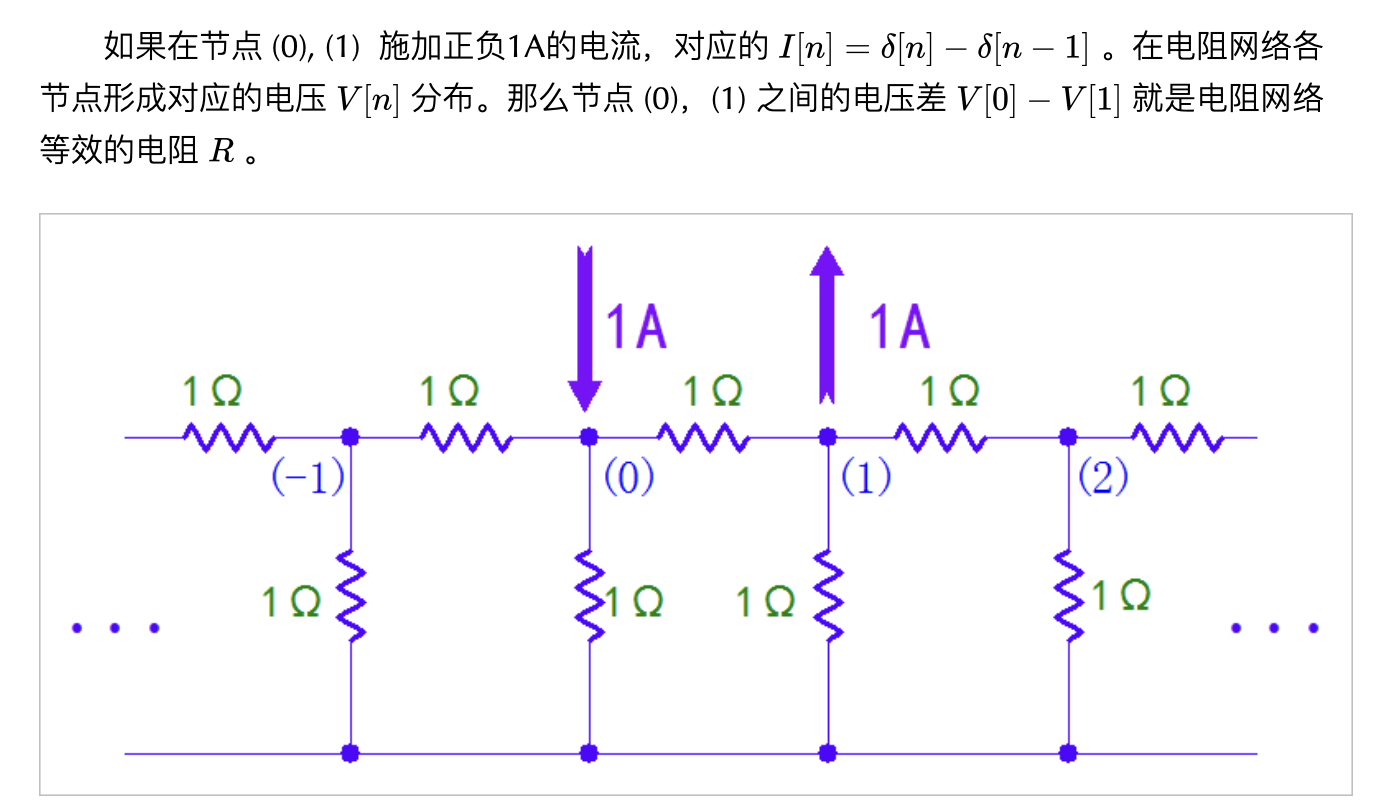
▲ 图1.1.5 每个节点对应的电压与电流

▲ 图1.1.6 在相邻两个节点施加正负1A电流激励

三、利用Z变换求解

1、z变换方程

 

2、留数定理求取积分

上述积分通过留数定理进行求取。积分公式中包含有三个极点  

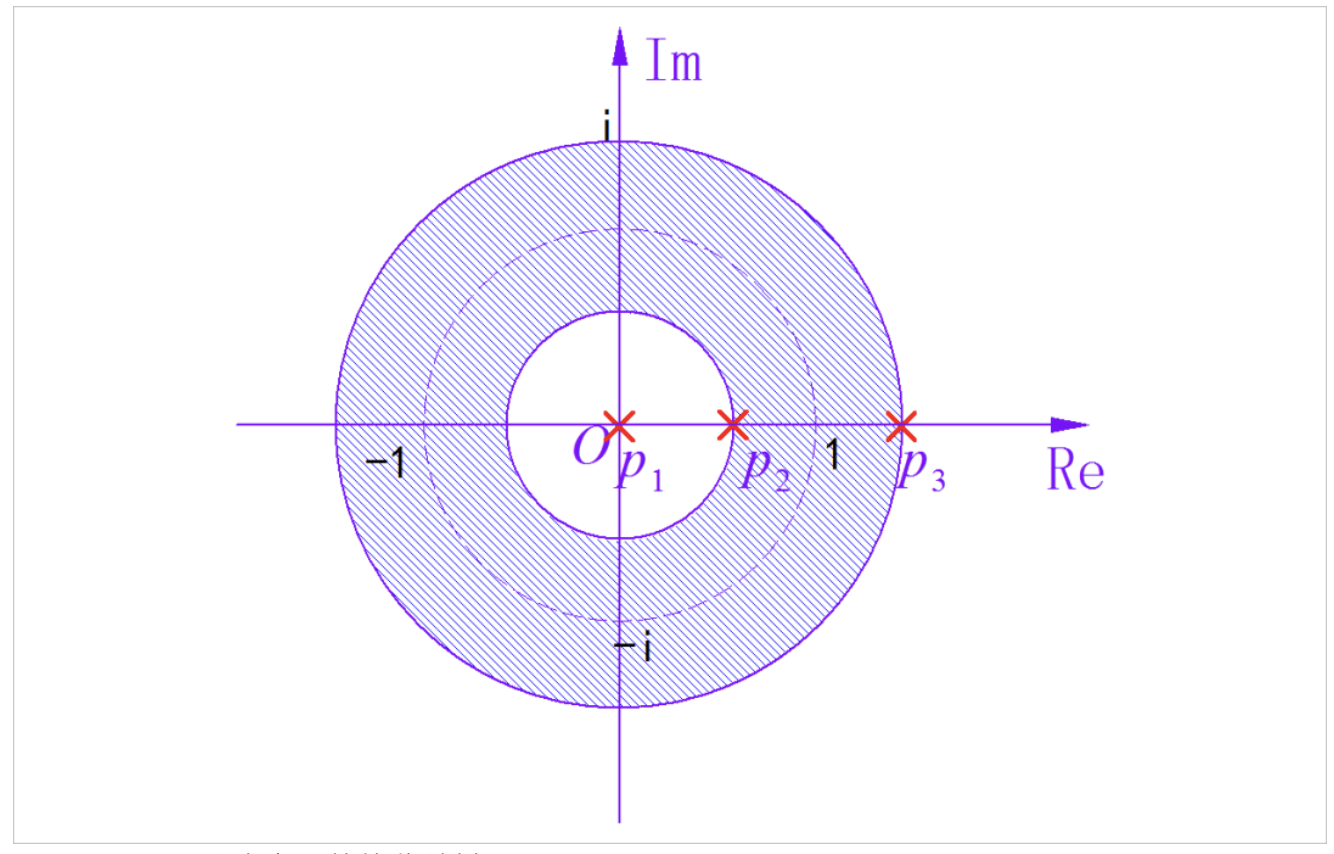
根据上述分析，可以知道积分号中的被积函数的收敛域只能如下图所示。

▲ 图1.3.1 积分式内函数的收敛域

所以，对应的围线积分的路径中只包含有两个极点。这两个极点对应的留数分别为  

        所以相邻节点之间的电阻为：

02DFT与ZT
 

  可以看到最后计算时，利用留数定理计算最终的积分值比较方便，避免了比较复杂的三角函数的积分计算。但在分析被积函数的收敛域的时候，需要比较小心。

※总  结 ※

这学期的信号与系统进展到第五章，拉普拉斯变换与 z 变换。前几天看到一篇博文中对于无限电阻网络求解相邻节点阻抗中使用了离散傅里叶变换 (DFT) 的方法比较新颖。分析了DFT在其中仅仅是起到描述线性时不变离散时间系统的作用，所以将其替换成 z 变换进行描述，则在分析求解过程中会更加的清晰。

作者：TsinghuaJoking
文章来源：卓晴

审核编辑 黄昊宇