如何使用ADuC706x 实现基于MCU的RTD传感器接口

实现铂电阻温度检测器 (RTD) 的极高精度需要极其精确的信号调理和处理。本文介绍如何使用 ADuC706x 和几个无源组件实现基于 MCU 的 RTD 传感器接口。

铂电阻温度检测器 (RTD) 是最精确的传感器之一，可用于测量 –200°C 至 +850°C 范围内的温度。RTD 能够实现 ±0.02°C 或更高的校准精度。然而，要获得最大程度的准确度，需要精确的信号调理、模数转换、线性化和校准。

Analog Devices, Inc. MicroConverter® 产品系列包括在单芯片中具有 24 位 ADC 和 32 位 ARM7 MCU 的器件，信号调理电路非常适合 RTD 传感器。

本应用笔记介绍了如何使用ADuC706x和几个无源元件实现完整的 RTD 传感器接口。本应用笔记基于 AN-709 应用笔记、使用 ADuC8xx MicroConverter 的 RTD 接口和线性化。

强烈建议使用本应用笔记中引用的软件实用程序和示例代码来实现基于 MicroConverter 的 RTD 传感器接口。
硬件设计

RTD 是一种传感器，其电阻以精确定义的方式随温度变化。在尝试了解 RTD 温度电阻传递函数（非线性）的详细信息之前，假设非线性是经过数字校正的。然后，专注于将 RTD 电阻转换为数字值。一种常用的方法如图 1 所示

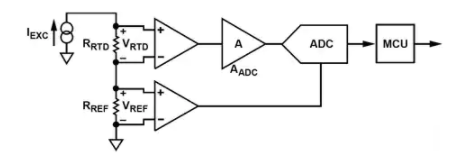
图 1：RTD 接口硬件配置。

在图 1 中，单个电流源 (I EXC ) 通过串联方式激励 RTD (R RTD ) 和精密参考电阻 (R REF )，产生 ADC 输入电压 (V RTD ) 和参考电压 (V REF），分别。

ADC 的归一化数字输出（零输入 = 0 和满量程输入 = 1）只是输入电压与参考电压的比率乘以增益级 A ADC。

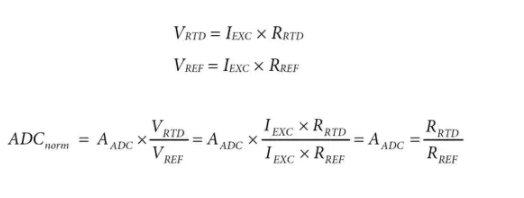
注意我是如何EXC抵消了上述等式。这意味着即使激励电流发生变化或不精确，ADC 结果始终直接对应于 RTD 电阻与参考电阻的比率。选择一个精密、低漂移的参考电阻意味着 RTD 电阻可以非常精确地知道，即使电流源的精度要低得多。

使用 MicroConverter 应用同样的原理，图 2 显示了 ADuC706x 连接用于与 4 线 RTD 接口。请注意，这与图 1 所示的总体拓扑相同，除了所有有源组件（励磁电流源、V RTD和 V REF的差分输入级、增益级 A ADC、ADC 本身和微控制器）都包含在 ADuC706x 芯片内部。二极管保护和 100Ω 电阻仅用于保护 ADuC706x 在端子块出现过压情况时免受损坏。

还包括其他外围设备，例如用于数字通信路径的串行通信端口。另请注意，添加了一些无源元件用于信号的 R/C 滤波和端子块处的过压保护。这代表了一个完整的实现，只需要一个电源和数字接口所需的任何特定外围芯片，例如 RS-232 或 RS-485 线路驱动器/接收器。

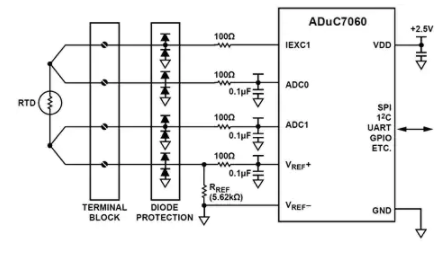
图 2：使用 ADuC706x 的完整 RTD 接口电路。

根据 ADC 结果计算 RTD 电阻

如硬件设计部分所述，

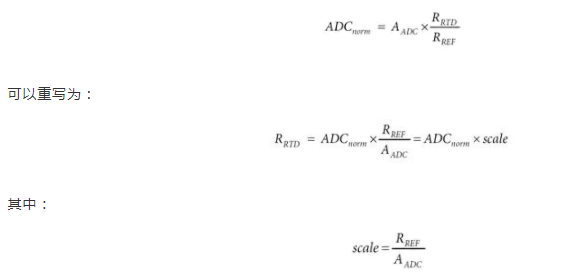
比例值是示例代码中使用的固定比例因子。更进一步，可以将固定偏移值添加到等式中，从而得出

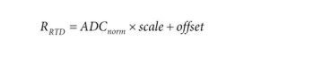
偏移项表示可用于补偿误差的固定偏移。这个偏移项将在校准部分进一步讨论。在大多数情况下，该偏移项的值为零就足够了。请注意，RTD 电阻的直接方程是作为 ADC 结果的函数，仅使用一对固定的比例和偏移值。

本应用笔记的其余部分考虑最常见的铂 RTD 类型，其在 0°C 时的标称电阻 (R 0 ) 为 100Ω。使用本应用笔记时，假设参考电阻值为 5.62 kΩ，它可以很好地匹配这种 RTD。有了这些组件值，并使用 ADuC706x，32 的内部增益是最高可用 ADC 增益设置，它仍然允许 RTD 覆盖其完全指定的温度范围。

请记住，ADC范数被限制在 0 到 1 的范围内，这定义了较高 ADC 增益下的温度范围限制。32 的增益对应于 0x8415 的 ADC0CON 值，或 37.5 mV 单极的范围设置，其中：

为了对应这个增益设置，比例值计算为 175.625，其中：

这是示例代码中使用的默认比例值。偏移项的默认值为零。这些等式假设 IEXC0 引脚上的激励电流为 200 µA。这是通过设置 IEXCCON = 0x42 来配置的。

本节中 R RTD的公式只是通过软件直接根据给定 ADC 转换结果确定 RTD 电阻的方法。要将 RTD 温度确定为其电阻的函数，需要了解 RTD 传递函数。

RTD 传递函数

铂 RTD 传递函数由两个不同的多项式方程描述：一个用于低于 0°C 的温度，另一个用于高于 0°C 的温度。

请注意，符号从 R RTD更改为 R RTD(t) 反映 RTD 电阻是其温度的函数。图 3 显示了 RTD 传递函数（电阻绘制为温度的函数）以及传递函数斜率在 0°C 时的线性扩展（用于视觉比较）。

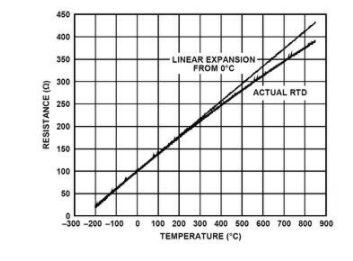
图 3：RTD 传递函数。

前面的公式将 RTD 电阻定义为温度 R RTD (t) 的函数。但是，要实现 RTD 传感器接口电路，必须将 RTD 温度确定为其电阻 T RTD (r) 的函数。考虑到 RTD 的非线性传递函数，这可能不太直接。以下部分探讨了此任务的有用技术。

线性化技术

在给定 RTD 传递函数的情况下，有许多不同的方法可以将温度确定为 RTD 电阻的函数。本应用笔记探讨了三种在嵌入式设计中有用的技术。这些技术特别适合基于 MicroConverter 的设计。表 1 概述了每种方法的优缺点。此处显示的执行时间代表 ADuC7060 在核心时钟速度为 10.24 MHz 下运行此处引用的 C 子程序的经验测量值。

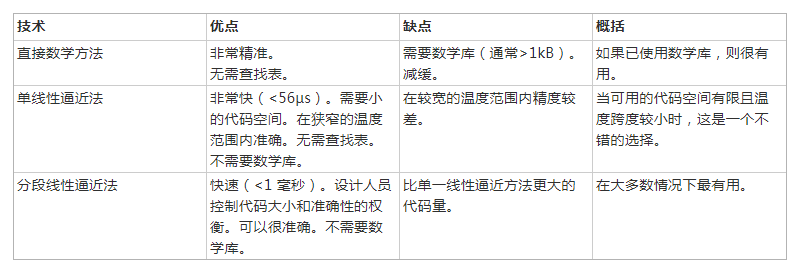
表 1：线性化方法的比较。

直接数学方法

在 RTD 传递函数部分，显示了作为温度函数 R RTD (t) 的 RTD 电阻的明确数学方程。是否可以将这些方程反过来并求解 RTD 温度作为其电阻 T RTD (r) 的函数的表达式？对于定义正温度行为的方程来说，这是一项相当简单的任务，因为它只是一个二次方程。二次方程的解产生两个表达式；要确定哪一个是正确的，只需替换几个已知值。对于 0°C 或更高温度下的 RTD 温度，结果为以下公式：

这有利于实时计算，因为 Z 1到 Z 4是常数和绝对值，因此需要较少的计算。上述 T RTD等式(r) 被称为正函数，因为它与 0°C 及以上的温度有关。由于这是一个直接的数学解决方案，因此在该范围内它是 100% 准确的。求解该等式时，在 ARM7 C 代码中使用 32 位浮点数学运算的舍入误差约为 +0.0001°C/–0.0005°C。这对于任何实际目的来说都足够接近 100% 的准确度。当使用内核时钟速度为 10.24 MHz 的 ADuC706x 运行 RTDmath.c 的示例 C 例程时，该等式的执行时间小于 750 µs。

前面的公式仅适用于 0°C 及以上的温度。R RTD的方程定义负温度行为的 (t) 是一个四阶多项式（在扩展第三项之后），并且对于求解作为电阻函数的温度的单一表达式是不切实际的。然而，利用计算机数学工具可以帮助找到逆传递函数的近似值。

使用 Mathematica® 或类似的软件数学工具为 0°C 或更低温度下的 RTD 温度得出以下最佳拟合多项式表达式：

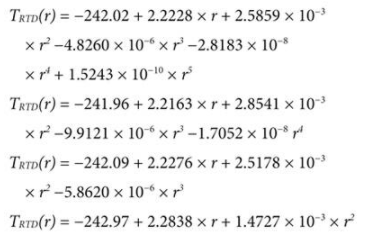
这四个方程被称为负函数，因为每个方程仅适用于 0°C 及以下的温度。顶部（五阶）方程最准确，但计算时间最长，而底部（二阶）方程精度最低，但计算速度最快。表 2 给出了这些负函数的一些特性，图 4 显示了每个函数的误差随温度变化的曲线，以及（供视觉参考）正函数的误差扩展到负温度空间。

请注意，在图 4 中，在接近零的负温度下，正函数的误差实际上比二阶、三阶或四阶负函数的误差要小。示例代码 RTDmath.c 通过使用正函数来利用这种行为，即使在稍微负的温度下也是如此。确定应使用正函数还是负函数的实际阈值因使用的负函数（二阶、三阶、四阶或五阶）而异，并在表 2 的阈值列中表示。这个阈值，正函数产生较低的误差；低于此阈值，负函数会产生较低的错误。表 2 中的方程式精度列仅代表低于相应阈值的温度的误差。

¹执行时间和方程精度是在 ADuC706x 上以 10.24 MHz 的核心时钟速度运行 RTDmath.c 的示例 C 例程的经验测量的。

表 2：最佳拟合多项式方程（负函数）的特征。

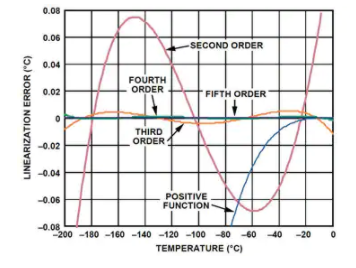
图 4：最佳拟合多项式方程（负函数）的误差图。

用于线性化的直接数学技术的一个缺点是它需要浮点幂和平方根函数，例如 IAR Systems 的 IAR 编译器的数学库中的函数。仅这些浮点数学函数通常会增加超过 1kB 的代码大小。使用分段线性逼近方法部分中描述的分段线性逼近方法，可以使用更小的整体代码大小实现相似或更高的准确度。但是，如果程序中的其他操作需要数学库函数，则直接数学技术可能是最佳解决方案，因为这些库函数已经可用。

单线性逼近法

在图 3 中，请注意，在较小的温度范围内，RTD 传递函数类似于一条直线。如果所需的测量温度范围仅跨越整个 RTD 测量频带的一部分，则可能根本不需要对 RTD 信号进行线性化。在这种情况下，在所需测量温度范围内对传递函数进行最佳拟合线性近似通常可以产生足够的精度。例如，在 –40°C 至 +85°C 的工业温度范围内，最佳拟合线性近似值精确到 ±0.3°C。

一般来说，作为 RTD 电阻 (r) 函数的温度线性方程具有以下形式：

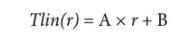
其中 A 和 B 是常数。

请注意，这些与 RTD 传递函数部分中描述的 A 和 B 不同。为 A 和 B 选择最佳值以最小化误差带涉及一些此处未探讨的数学。但是，本应用笔记附带了一个非常简单的软件工具，它可以自动找到适合您特定温度范围的 A 和 B 的最佳值。本应用笔记中对该工具进行了检查，但首先必须确定单个线性近似是否适合特定的设计要求。

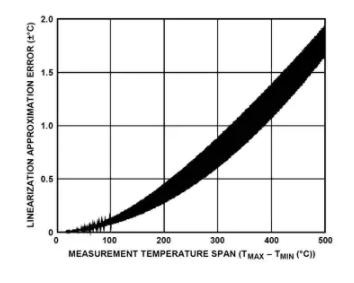
图 5：单一线性近似误差与测量温度跨度的关系。

图 5 显示了在高达 500°C 的测量温度范围内产生的总近似误差。对于超过 500°C 的跨度，近似误差会随着温度跨度的增加而继续降低。图 5 曲线的不精确性（即数据迹线的宽度）是由于即使对于相同的温度跨度，不同绝对温度带的误差也是不同的。例如，–200°C 至 0°C 和 +600°C 至 +800°C 温度范围的精度不同，即使它们的精度都为 200°C。

图 5 提供了一个粗略的误差概念，以帮助衡量是否应将单一线性近似视为一种选择。如果确定它可能是一个选项，则 RTD 系数生成器工具（在 RTD 系数生成器工具部分中描述）可以帮助确定特定温度范围的实际近似误差，并且可以生成针对该温度范围优化的源代码。

分段线性逼近法

将线性逼近更进一步，可以将任意数量的线性段概念化，以更好地逼近非线性 RTD 传递函数。生成这一系列线性段以使每个段的端点与相邻段的端点相交，从而可以将其视为由直线连接的多个点。这些点（或系数）可以计算一次以最好地匹配 RTD 的非线性传递函数，然后永久存储在 ROM 或闪存中。从这个系数表中，MCU 可以执行简单的线性插值，以根据测得的 RTD 电阻确定温度。

要了解这在实践中是如何实现的，首先假设系数表已经存在。表中的每个系数只是传递函数上的一个点，由电阻和温度表示。因此，该表采用以下形式：

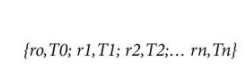
给定此表，MCU 的实时任务（确定给定电阻 r 下的温度）首先确定哪两个系数最接近所讨论的点（称为 {rm ,Tm} 和 {rn,Tn})，然后在这两点之间进行线性插值以求解温度。该范围的实际线性插值公式（即，仅对 r m和 r n之间的 r 值有效）采用以下形式：

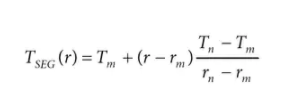
请注意，上述查找表中的每个系数都由两个数字组成，一个代表电阻，一个代表温度（本质上是传递函数中的 x 和 y 值）。因此，对于 N 个线性段（即 N + 1 个系数），总共必须将 2N + 2 个值存储在内存中。为了减小查找表的大小，考虑一个由 N 个段组成的表，每个段跨越相等的电阻宽度。这样的表只能存储为一组温度点，如下所示：

{T0; T1; T2; ... tN}

因为对于给定的系数 {r n ,T n }，可以通过以下方式计算 rn 的值：

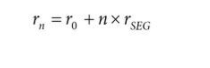
其中：

r 0和 r SEG是固定值，与系数表一起存储在 ROM 中。

r 0是系数为零时的电阻{r 0 ,T 0 }。

r SEG是分隔相邻系数的固定电阻跨度。

然后，给定段的线性插值公式变为

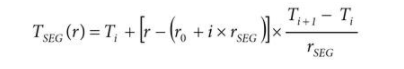
其中 i 表示正在使用哪个段（即，哪对系数），并使用 r 的值计算如下：

同样，上述 T SEG (r)的表达式只不过是两个系数 T i和 T i + 1之间的线性插值。为了在实践中实现这一点，MCU 必须首先求解 i（根据最后一个方程），以便系数 T i和 Ti + 1是最接近 r 输入值的两个。然后，通过 i 求解，MCU 可以简单地求解 T SEG (r) 方程以确定给定输入电阻下的温度。

这种分段线性逼近技术产生的总体误差取决于段的数量（或系​​数的数量，或查找表的大小）以及温度的总体跨度。

图 6 显示了测量温度范围为 –200°C 至 +850°C 的线性近似误差与查找表大小的函数关系（使用 RTD 系数生成器工具生成的优化系数）。请注意，如果减小测量温度范围，则在查找表相同大小的情况下会产生更好的误差，或者在查找表较小的情况下会产生相同的误差。

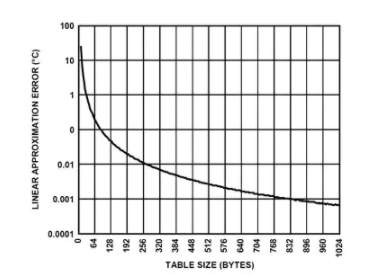
图 6：分段线性逼近误差与查找表大小的关系（-200°C 至 +850°C 范围）。

RTD 系数生成器工具

实现分段线性化函数最困难的部分是生成查找表。但是，本应用笔记随附的 RTD 系数生成器工具 (coefRTD.exe) 会自动为铂金 RTD 执行此操作。这个简单的 DOSexecutable 使用分段线性或单线性逼近方法协助基于 ARM7 的 RTD 接口设计。它执行以下任务：

• 为给定的温度范围和查找表大小生成优化的查找表系数。
• 指示产生的误差带和查找表大小。
• 在 ARM7 C 源代码中生成完整的 RTD 线性化函数（包括查找表）。
• 根据给定的查找表生成一个误差值表作为温度的函数。

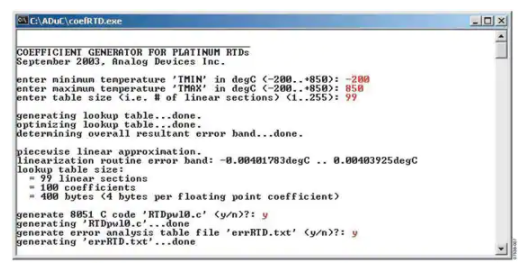
图 7：具有分段线性近似的系数生成器会话示例（用户输入为红色）。

图 7 显示了一个带有用户输入的示例会话。请注意，该程序只要求用户输入三个参数（T MIN、T MAX和 N SEG）。该程序可以生成文件 RTDpwl0.c，它是一个完整的 C 源文件（一个定制的、用户特定的查找表），可以按原样包含在一个项目中，其中 T_rtd() 函数可以直接从函数中调用其他源文件。或者，可以将 RTDpwl0.c 的任何部分直接复制并粘贴到其他源文件中。

系数生成器还可以输出错误分析文件 (errorRTD.txt)，这是一个制表符分隔的文本文件，可以导入 Microsoft® Excel 或任何其他电子表格程序，以检查线性逼近例程生成的错误。

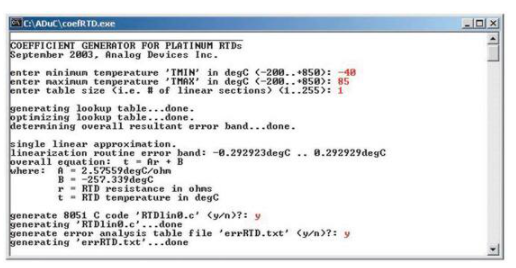
图 8：具有单一线性近似的系数生成器会话示例（红色为用户输入）。

系数生成器程序不仅为分段线性逼近生成线性化函数，还为单线性逼近生成线性化函数。为此，请为表格大小输入 1 以仅指示单个线性段。

程序识别这一点并输出与单线性逼近方法而不是分段线性逼近方法相关的结果，如图 8 所示

ADuC706x 具有内置功能，用于校准 ADC 的端点误差（偏移和增益误差），如产品数据表中所述。但是，如果在校准过程中考虑到整个信号链，包括 RTD 本身，最终可能会得到较低的总体误差，在这种情况下，内置 ADC 校准不会提供额外的好处。本应用笔记首先检查整体校准，然后指出内置 ADC 校准可能仍然有用的一些情况。

到目前为止，假设 RTD 本身是完美的。然而，真正的 RTD 并不完美。就像现实世界中的其他任何东西一样，它们也有与它们相关的错误，如 RTD 制造商的数据表所指定。幸运的是，这些错误中的许多都可以在软件中轻松校准。本应用笔记中讨论的校准功能可用作单点校准或两点校准。该函数可以与任何线性化技术结合使用。

要了解单点校准原理上的工作原理，请参阅 RTD 传递函数部分中讨论 R RTD (t) 的位置，并注意它主要由值 R 0定义，即 RTD 在 0 时的电阻摄氏度。对于最常见的 RTD，R0标称 100Ω。但是，此 R 0值是 RTD 传感器中最重要的误差源，因为它可能因设备而异。此外，由于 R 0值简单地乘以 R RTD (t) 表达式中传递函数的其余部分，因此由 R 0容差引起的误差纯粹是相乘的，因此可以通过调整R RTD作为归一化 ADC 转换结果的函数的以下表达式（如前所述） ：

具体而言，如果可以将 RTD 带到非常精确的已知温度并执行 ADC 转换，则校正后的比例值可以计算为：

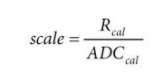
其中 ADC cal是模数转换的实际归一化结果，R cal是该 RTD 温度下的理想（预期）电阻值。R cal可以使用 R RTD (t)的公式手动计算。通过这种方法（称为单点校准），获得校正的刻度值，补偿 RTD R 0容差，同时也补偿参考电阻的初始容差。为了更进一步，可以采用两点校准，它不仅可以补偿这些缩放误差，还可以补偿可能存在的任何偏移误差。这样做不仅需要调整比例值，还需要调整偏移值。

假设已经执行了单点校准，现在可以将 RTD 带到第二个非常精确的已知温度，并执行另一个 ADC 转换。标度值的公式（即 R RTD与 ADC范数函数的斜率）为：

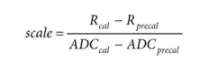
其中：

R precal和 ADC precal分别是前一个校准点的电阻和 ADC 转换结果。

对于当前校准点， R precal和 ADC precal相同。

请注意，这是一种确定 R RTD与 ADC标准斜率的方法使用该线上的两个点传递函数。只需注意偏移值，因为现在已知比例值，所以可以使用单个点来确定偏移值。偏移值的以下表达式通过求解上述 R RTD表达式的偏移，然后分别用 R precal和 ADC precal替换 R RTD和 ADC norm得出。 请注意，如果 R precal和 ADC precal

都为零（表示没有先前的校准点），则刻度值的表达式与单点校准相同，偏移值的表达式为零，就像这是单点校准一样。因此，相同的函数（示例代码中的 Cal()）可用于执行单点校准或两点校准。

如果按原样使用示例代码，请按照以下步骤执行 2 点校准：

1. 选择两个温度进行校准，确保温度点充分分开（理想情况下至少为总测量跨度的四分之一），以避免在测量温度范围的极端附近累积误差。
2. 将 RTD 带到第一个温度点，等待显示结果稳定到新值，然后按终端（或终端仿真器）上的任意键以显示用户 I/O 菜单。
3. 按照菜单提示校准到已知温度，然后在出现提示时输入温度。
4. 对第二个温度点重复步骤 2 和步骤 3。

注意：对于单点校准，请跳过第 4 步。

虽然校准有很多好处，但也有许多系统考虑因素使其在某些应用中不切实际。如果无法按照步骤 1 至步骤 4 中的说明执行校准，请考虑执行系统 ​​ADC 校准，如 ADuC706x 数据手册中所述。为此，请将 RTD 更换为短路电阻 (0Ω) 并触发系统零刻度校准。然后，用高精度 719.36Ω 电阻替换 RTD 并触发满量程校准。这补偿了内部 ADC 误差和 RREF 电阻的初始容差，但不考虑 RTD 本身的任何误差。

请注意，ADuC706x（和所有其他 MicroConverter 产品）的另一个好处是它包含片上非易失性闪存，可用于存储校准的比例和偏移值。这样，芯片可以在每次系统上电时恢复校准值，而不是每次系统上电时都需要进行校准。

错误分析

数据采集​​设计有许多误差源，例如 ADC 线性度、输入放大器噪声、电阻器约翰逊噪声、放大器温度漂移和电阻器温度漂移。确定给定设计中哪些占主导地位可能是一项艰巨的任务。幸运的是，ADuC706x 将所有有源级集成到一个完全由工厂指定的器件中，使误差分析成为一项简单得多的任务，但仍需要深入了解涉及非线性传感器元件的设计。本应用笔记探讨了迄今为止讨论的特定硬件和软件配置中最重要的几个错误组件。

如果系统未针对特定 RTD 进行校准（使用单点或两点校准），则 RTD 本身几乎肯定是绝对误差的最重要来源。该误差应在 RTD 制造商的数据表中很好地量化，取决于所选 RTD 的具体型号。本应用笔记主要关注 RTD 本身以外的错误源。

噪音

要检查的一种错误是噪声。在此设计中需要考虑三个主要噪声源：电阻约翰逊噪声、放大器/ADC 输入电压噪声和放大器/ADC 输入电流噪声。这些加在一起为平方和，因此当一个噪声源甚至比另一个噪声源稍大时，贡献较小的源可以忽略不计。在这种特定情况下，主要噪声源恰好是放大器/ADC 输入电压噪声。具体而言，在讨论的增益设置下，ADuC706x 输入电压噪声规格为 0.25 µV rms，或约 1.65 µV pp。

将此输入电压噪声转换为产生的输出温度噪声可能并不直观，并且由于非线性电阻-温度传递函数，会导致温度噪声随 RTD 温度而变化。结果如图 9 所示。

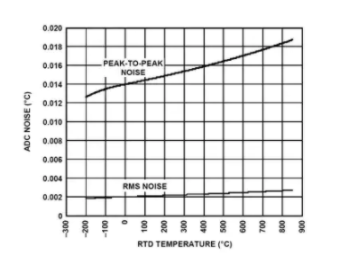
图 9：ADC 噪声与 RTD 温度的关系。

请注意，即使在最高 RTD 温度（即最差噪声）下，峰峰值噪声也始终低于 0.013°C；在较低的测量温度下甚至更好。请记住，这种作为 RTD 温度函数的噪声变化不是 ADC 本身的函数，而是数字域中实现的非线性 T RTD (r) 传递函数的直接结果。

温度漂移

另一个需要考虑的误差来源是温度漂移。具体来说，ADC 失调和增益温漂以及参考电阻温漂。这是直流误差（失调和增益误差）随 ADC 芯片或参考电阻温度变化的函数而变化。这与 RTD 调节电路的环境温度有关，而不是与实际测量的 RTD 温度有关。简而言之，这两个不同的温度在此分别称为环境温度和 RTD 温度。此外，由于非线性 T RTD (r) 传递函数，温度漂移值（即对环境温度的敏感性）随 RTD 温度的变化而变化。图 10 所示的结果需要一些解释。

图 10 的 x 轴是 RTD 温度。y 轴是温度漂移（以°C 为单位），环境温度每变化°C 时测量误差的变化。例如，如果 RTD 温度固定在 100°C，则 V REF漂移（使用 5 ppm/°C 参考电阻）约为 ±0.01°C/°C。因此，如果环境温度变化例如 50°C，则测量温度读数的变化幅度可能高达 ±0.5°C（忽略温度漂移的其他因素）。

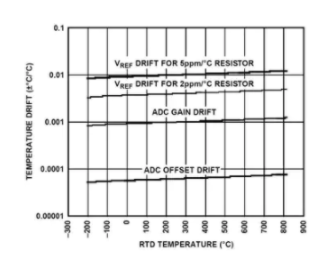
图 10：温度漂移与 RTD 温度的关系。

很明显，在环境温度范围通常跨越 -40°C 至 +85°C 或更高的工业环境中，温度漂移可能是相当重要的误差源。使用 ADuC706x 的片上温度传感器可以直接测量芯片温度（密切跟踪环境温度），然后使用该测量的芯片/环境温度来补偿温度漂移误差。

这需要在制造过程中进行额外的温度循环步骤，特别是使环境温度达到两个固定值，并在每个环境温度下获取零刻度和满刻度 ADC 读数。然而，软件可用于在温度传感器精度和参考电阻器与 ADuC706x 之间的温度梯度范围内补偿温度漂移误差。本应用笔记没有进一步探讨这种温度漂移补偿技术。但是，请注意，片上资源的存在使此选项成为可能，只需更改软件即可。

RTD自加热

RTD 自热是另一个需要考虑的误差来源。简而言之，通过 RTD 施加电流会导致其耗散功率，从而提高 RTD 的温度。幸运的是，由于 RTD 的激励电流仅为 200 µA，因此对于 100 Ω R 0，RTD 消耗的总功率永远不会超过 8 µW 。由这种小功率耗散引起的自热量会有所不同，具体取决于所使用的 RTD 的具体型号，但通常可以忽略不计。

其他错误来源

其他错误来源大多可以忽略不计。直流端点误差（偏移和增益误差）可以使用校准部分中讨论的校准技术进行完全校正。电阻约翰逊噪声远低于 ADC 的输入电压噪声。唯一值得考虑的其他误差源是 ADC INL（积分非线性或相对精度）。ADuC706x 数据手册的典型 INL 规范为满量程的 15 ppm，这导致输出参考 INL 误差约为图 9 所示峰峰值输出噪声值的两倍。