用蒙特卡罗仿真数据来检查元件容差如何影响级联电路网络的电气行为

专业电路设计人员在设计电路时不仅仅使用并联和串联的元件。构建电路的一种方法是使用具有输入和输出端口的电路网络。可以通过传统方式（SPICE、手动等）分析每个网络内部发生的情况，但重要的是网络将输入电压/电流对映射到输出电压/电流对。在数学上，这可以用传递函数进行量化。

在进行高可靠性设计时，需要了解的一个重要因素是系统某一部分的方差如何传播到系统的输出。但这个因素有时并不直观。它需要手动进行一些数学推导，或者需要一些仿真来确定系统中电气行为的变化和波动。

在本文中，我将展示如何使用蒙特卡罗仿真数据来检查元件容差如何影响级联电路网络的电气行为。数学涉及几个常见的概率论要点，但最终结果和所涉及的过程可以很容易在SPICE和Excel中实现。

01 理论：级联网络中的方差    

接下来我要介绍一个理论，目的是推导出表达式，该表达式将级联网络的输出电压变化定义为每个网络中各个传递函数的变化。尽管还有温度或随机噪声等情况，我们假定网络传递函数的变异仅由元件容差造成。

首先，让我们来看下面所示的级联网络。在这个网络，我们考虑的方案中每个网络有2个端口（输入和输出）。扩展到3个端口稍显复杂，但如果其他端口只是固定的功率输入，我们仍然可以使用此处所示的理论。级联中每个网络都有一个传递函数H。

网络输入和输出之间的关系如方程式(1)所示。在这个方程式中，整个网络的传递函数是每个网络传递函数的乘积：

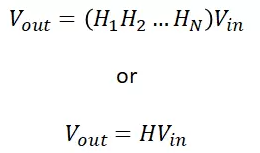
方程式(1)：级联网络传递函数定义。

在方程式(1)中，我们的事实依据是，如上所示的串联级联网络的总传递函数是所有单个传递函数的乘积。这个方程适用于构建为二端口网络的各种电路。现在，我们可以检查给定元件容差值的传递函数中的统计变化。

02 转移函数的变量    

每个网络中的元件容差将在每个网络中的传递函数中产生一些变化。我们现在要定义传递函数中的方差。

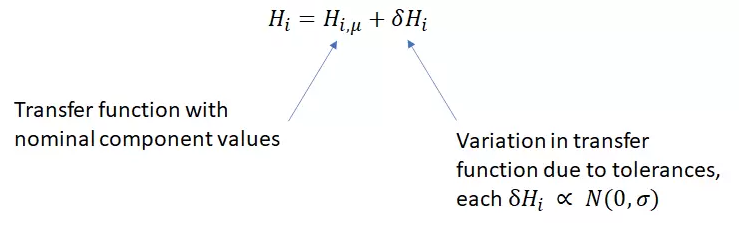
方程式(2)：每个网络的传递函数定义为常数部分（平均值）和随机部分（标准差）。

在方程式（2）中，Hi是一个随机变量，它与网络i（ẟHi）传递函数的随机变化有关。为了使该表达式为真，分布ẟHi必须允许这种类型的线性转换。一般来说，高斯分布和均匀分布都是如此，因此这在蒙特卡罗仿真中经常考虑的两种主要情况下都是有效的。

我们没有将ẟHi与具有特定等式的元件公差联系起来。但是，如果您知道电路网络中所有元件的公差，则可以使用蒙特卡罗仿真来确定ẟHi。只需为单个网络 Hi 进行仿真，然后运行蒙特卡罗仿真以确定传递函数 ẟHi 的方差。

03 输出电压的变量    

现在我们已经定义了单个传递函数的随机变量，我们可以通过将公式(2)中所示的相同线性变换应用到公式(1)中的传递函数的乘积来定义输出电压的变量。我将其写成公式(3)：

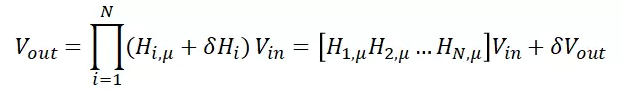
公式(3): 输出电压的变量。

这里，输出电压也有常数部分（平均值）和随机部分（标准差）。换句话说，现在电压是一个与随机变量乘积相关的随机变量。平均输出电压是右侧的常数项：

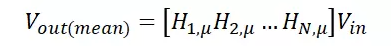
方程式(4)：根据组成级联网络的传递函数平均值表示的平均输出电压。

由此可知，传递函数的乘积是整个网络传递函数的平均值：

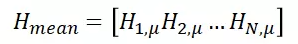
方程式(5)：整个级联网络的传递函数平均值以级联中各个网络的平均传递函数值表示。

如果我们展开方程式(3)中的乘积，将得到一个包含多个ẟHi 项、Hmean 和输出电压方差的乘积的表达式。在这里，我们将采取近似值，因为任意ẟHi项的乘积非常小，可以忽略不计。考虑到常见的元件公差，这是完全可以接受的，即使它们高达 20%。这里我就省略中间步骤，留给读者自行运算，最终可以得到以下方程式：

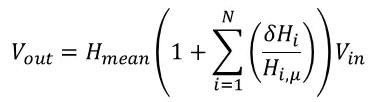
方程式(6)：以传递函数均值和随机变化表示的输出电压。

这看起来不像最终答案，但是方程式(6)确实告诉您在传递函数存在一些差异的情况下，您需要了解有关输出电压随机行为的所有信息！在这里，我们根据随机变量的线性组合（ẟHi 项集）定义了一个随机变量（Vout）。从多元概率论中，我们知道这个和的标准差等于ẟHi 项的正交和。换句话说，Vout 的标准偏差为：

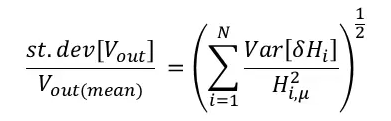
方程式(7)：输出电压基于传递函数方差的标准差。

在这个方程式中，st.dev运算指标准差，Var运算指方差。使用方程式(7)，我们可以开发一个仿真过程，将输出电压的变化与级联网络中传递函数的变化联系起来。

04 过程    

现在我们可以开发一个根据传递函数方差来确定输出电压方差的过程。您的主要工具将是蒙特卡罗仿真和简单的统计分析程序，如Excel：

1. 将级联网络电路设计划分为单独的二端口网络。

2. 针对#1中的每个网络运行蒙特卡罗仿真。

3. 获取每个网络的数据并计算每次蒙特卡罗运行的传递函数。

4. 计算每个网络的传递函数结果的平均值。

5. 计算#3中每个传递函数的标准差，得出每个网络的ẟHi。

6. 使用来自#4、#5和方程式(7)的结果，得出输出电压的变化。

根据您在此过程中使用的数据数量，您可以更进一步，得出结果的置信区间。 示例计算：

为什么要在单个传递函数上进行如此麻烦的运算？让我们来举个例子，了解其中原因。

假设您有三个具有不同元件容差（1%、5%和10%）的电路网络，并且您已经完成了上述过程以确定每个网络的传递函数的变化。假设这些元件公差值转化为下图中显示的示例方差。使用方程式(7)，我们可以预测这个假设网络的输出电压变化：

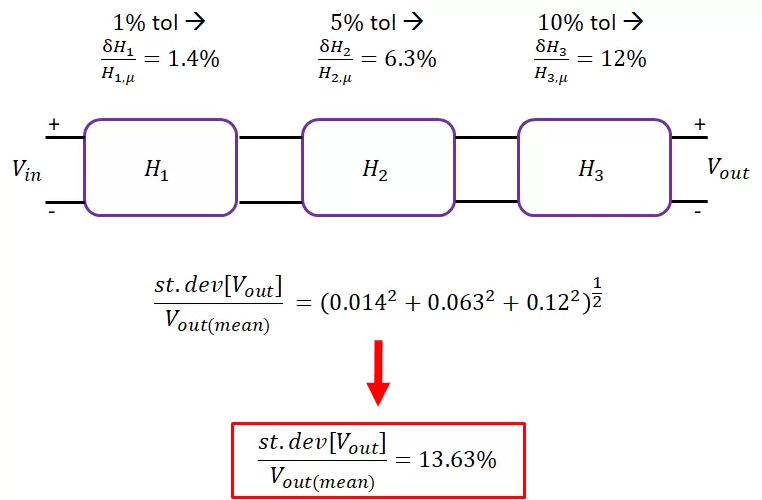
已知元件容差和传递函数变化的输出电压计算标准差示例。

根据应用，13.63%的容差可能过大。由此，我们可以判断是否应该降低某些元件组的容差。

现在假设输出电压变化对于我们的应用来说是不可接受的，我们希望得到更小的变化。我们决定将 5% 的容差和 10% 的容差换成 1% 的容差。无需运行任何新的仿真，我们就可以立即知道输出变化是什么。对于线性电路，将容差降低 10 倍应将传递函数方差降低 10 倍，对于其他降低因子，依此类推。然后我们会得到以下结果：

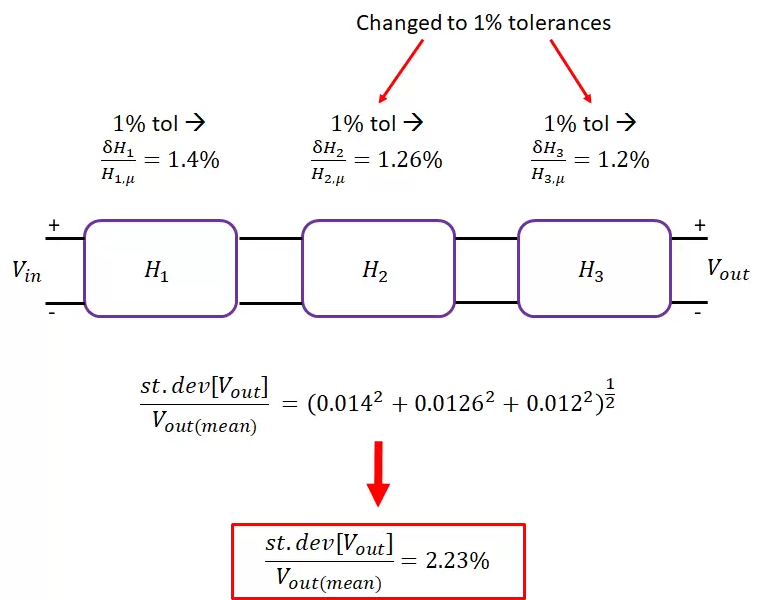
针对较小的元件容差，修改输出电压计算的标准差。

将输出电压从13.63%降低到2.23%，这一折减幅度非常大，而它所需要的只是一个简单的元件交换。无需添加新电路，无需更改设计，只需选择一些备用元件编号即可。这些类型的方差折减步骤正是您在精确仿真应用中所需要的。

现在假设您想改变运行频率。在这种情况下，您可以使用从蒙特卡罗仿真中获得的传递函数数据，使用相同的计算来确定在这个新频率下输出电压将如何变化。

05 总结与比较    

通过了解如何增加不同级联网络中的方差，得出输出电压的总方差，您可以执行以下任意操作，直接确定输出电压将如何变化：

将网络中的元件换成容差更严格的元件

把一个网络换成一个完全不同的网络

在级联中添加额外的网络

上面显示的扰动方法仅适用于串联级联滤波器或放大器。如果您有并行网络，它们的传递函数相加，使上面显示的方差分析更容易。此外，您可以使用这个想法来推导出串联和并联网络组合的方差表达式。无论您如何安排电路网络以获得方差表达式，都适用上述相同的仿真和分析方法。

如果您有兴趣在Altium Designer 内运行蒙特卡罗仿真和转移函数计算，可以在原理图编辑器中找到SPICE引擎中内置的仿真工具。完成 PCB 并准备好与合作者或制造商分享您的设计后，您可以通过 Altium 365 平台分享您完成的设计。设计和生产先进电子产品所需的一切都集成在一个软件包中。

审核编辑：刘清