

无源低通滤波器电路及计算公式
描述
滤波器是一种用于过滤信号的电路,它只会通过所需的信号并避免不需要的信号。通常滤波器由无源元件或有源元件设计,其中:
无源元件是电阻器、电感器和电容器。
有源元件是晶体管、FET和运算放大器。
低通滤波器是一种仅通过低频信号并衰减或停止高频信号的滤波器,它只允许来自0Hz的信号截止频率“fc”,该截止频率值将取决于电路中使用的组件的值。一般来说,这些滤波器在100 kHz以下是更可取的。截止频率也称为中断频率或翻转频率。
无源低通滤波器电路及计算公式
由无源元件设计的低通滤波器电路称为无源低通滤波器,下图显示了一个简单的RC低通滤波器电路:
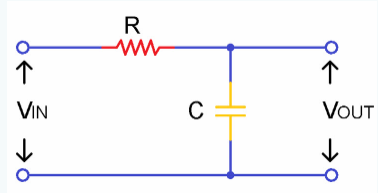
这里只需将电阻器“R”与电容器“C”串联,即可提供 RC低通滤波器。它可以简称为低通滤波器(LPF)。电阻器独立于电路中应用频率的变化,但电容器是一个敏感元件,这意味着它会响应电路中的变化。
由于它只有一个电抗元件,因此该电路也可以称为“单极滤波器”或“一阶滤波器”。输入电压“Vin”串联施加到电阻器,输出电压仅通过电容器。另外,电容器是敏感元件,因此要观察的主要因素是“容抗”。电容电抗是由于电路中的电容器而产生的反对响应。
为了保持电容器的电容量,电容器会反对电路中的少量电流流动。这种对电路中电流流动的反对称为阻抗。因此,容抗随着反向电流的增加而减小,由此可以说容抗与施加到电路的频率成反比。电阻器的电阻值是稳定的,而容抗值是变化的。与电容器的电压电位相比,电容器两端的电压降非常小。
这意味着在低频下,电压降很小,电压电位很大,但在高频下,电压降非常高,电压电位较小。通过这种现象,我们可以说上述电路可以充当“频率可变分压器”电路。
容抗可以表示如下:
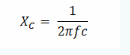
由于在该电路中,只有一个电容和一个电阻,所以电路中的阻抗可以通过以下公式计算:
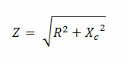
输出电压计算
为了得到分压器方程,必须考虑阻抗、容抗、输入电压和输出电压。通过使用这些概念,可以将RC分压器方程的方程表示如下:
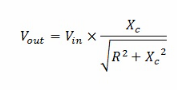
由于:
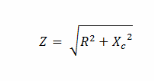
因此,可以将分压器方程写为:
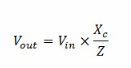
这样,通过使用这个等式,可以计算任何应用频率下的输出电压值。
根据实例计算可知,当频率增加时,容抗会减小,不仅容抗而且输出电压也会降低。
低通滤波器的滤波频率特性
从之前对滤波器的介绍中,可以看到滤波器的幅度 |H(jω)| 增益作为电路的增益。该增益测量为20 log (V out / V in ),对于任何RC电路,斜率“滚降”的角度为-20 dB/十倍频程相同。
截止区域以下的频带称为“通带”,截止频率之后的频带称为“阻带”。从下图中可以看出,通带是滤波器的带宽。
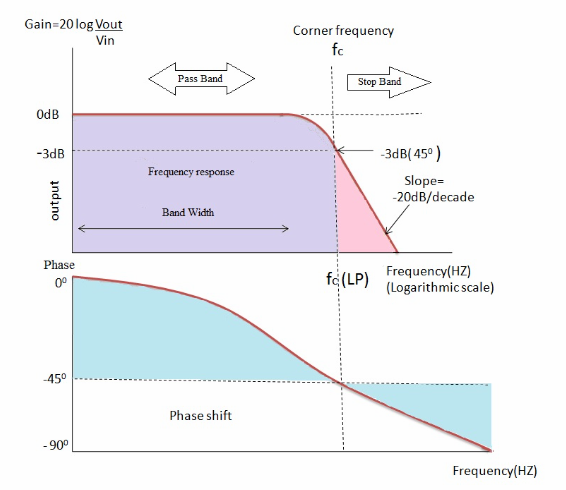
从该图中可以清楚地看出,在截止频率之前,增益是恒定的,因为输出电压与低频处的频率值成正比。这是由于电容电抗在低频下表现为开路,并允许最大电流通过高频电路。电容电抗的值在低频时非常高,因此它具有更大的阻止电流流过电路的能力。
一旦达到截止频率值,输出电压就会逐渐下降并达到零。增益也随着输出电压而降低。在截止频率之后,电路斜率的响应将达到-20 dB/十倍频的滚降点。这主要是由于频率的增加,当频率增加时,容抗值减小,从而阻止电流通过电容器的能力降低。当通过电路的电流增加时,由于电容器的电容有限,电路会起到短路的作用。因此滤波器的输出电压在高频时为零。
避免这个问题的唯一方法是选择这些电阻和电容可以承受的频率范围。电容器和电阻器的值起主要作用,因为这些值仅取决于截止频率“fc”。如果频率范围在截止频率范围内,那么就可以克服短路问题。
当电阻值和容抗值重合时,就会出现这个截止点,这意味着电阻和无功电容的矢量和相等。即当R=X c时,输入信号衰减 -3dB/decade。这种衰减约为输入信号的70.7%。电容器极板的充电和放电时间根据正弦波而变化。因此,输出信号的相位角 (ø) 在截止频率之后滞后于输入信号。在截止频率处,输出信号的相位为-45°。
另外,如果滤波器的输入频率增加,则电路输出信号的滞后角增加。简单来说,频率值越高,电路的异相就越多。由于正弦波的切换时间更长,电容器在低频下有更多的时间对极板进行充电和放电。但随着频率的增加,切换到下一个脉冲所花费的时间逐渐减少。因此,会发生时间变化,从而导致输出波的相移。
无源低通滤波器的截止频率主要取决于用于滤波电路的电阻和电容值。该截止频率与电阻和电容值成反比,其截止频率为:f c = 1/(2πRC)。
无源低通滤波器的相移为:相移 (ø) = – tan -1 (2πfRc)。
时间常数 (τ)
正如上面所述,电容器相对于输入正弦波对极板充电和放电所花费的时间会导致相位差。电阻和电容串联会产生这种充放电效果。串联RC电路的时间常数定义为电容器充电到最终稳态值的63.2%所用的时间,也定义为电容器放电到稳态值的36.8%所用的时间. 该时间常数用符号“τ”表示。
时间常数与截止频率的关系如下:
时间常数τ = RC = 1/2πfc 和 ω c = 1/τ = 1/RC。
当然,也可以用截止频率重写为:fc = 1/2πRC。由此可以说滤波器的输出取决于输入端的频率和时间常数。
二阶无源低通滤波器
上面介绍了由电阻和电容串联而成的一阶低通滤波器。然而,有时单级可能不足以去除所有不需要的频率,所以使用二阶滤波器,如下图所示:
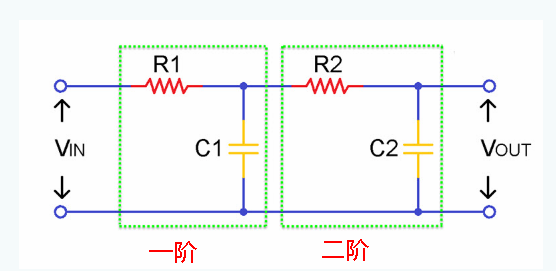
二阶低通RC滤波器可以简单地通过向一阶低通滤波器增加一个级来获得。该滤波器给出-40dB/decade或-12dB/octave的斜率,四阶滤波器输出-80dB/octave的斜率,依此类推。
无源低通滤波器截止频率处的增益为:A = (1/√2) n
其中n是阶段的顺序或数量。所以,二阶低通滤波器的截止频率可以写为:
fc = 1/ (2π√(R1C1R2C2))
二阶低通滤波器-3dB 频率为:f (-3dB) = fc √ (2 (1/n) – 1)
其中fc是截止频率,n是级数,f -3dB是-3dB通带频率。
低通滤波器简单小结
低通滤波器由电阻和电容组成。不仅电容器而且任何带有电阻的电抗元件都提供低通滤波器,它是一种只允许低频并衰减高频的滤波器。
低于截止频率的频率称为通带频率,高于截止频率的频率称为阻带频率,而通带是滤波器的带宽。滤波器的截止频率将取决于为电路设计选择的组件的值,截止频率可以使用以下公式计算:
fc = 1/(2πRC)
滤波器的增益作为滤波器的幅度,可以使用公式20log (V out / V in ) 计算增益。滤波器的输出是恒定的,直到频率水平达到截止频率。在截止频率下,输出信号为输入信号的70.7%,在截止频率后输出逐渐减小到零。输出信号的相位角滞后于截止频率后的输入信号。在截止频率处,输出信号相移为45°。
如果我们在低通滤波器电路中交换电阻器和电容器的位置,则电路的行为就像高通滤波器。对于正弦输入波,电路的行为类似于一阶低通滤波器。一阶滤波器的理论过程我们已经介绍了,但是当输入信号类型发生变化时,那么滤波器的输出会发生什么变化?
例如,当将输入信号类型更改为开关模式(开/关)或方波时,电路的行为就像一个积分器,下面简单介绍下。
低通滤波器作为波形整形电路
下图显示了滤波器对平方输入的性能,当低通滤波器的输入为方波时,得到的滤波器输出为三角形。
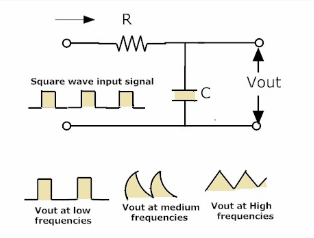
这是因为电容器不能用作ON或OFF开关。在低频下,当滤波器的输入为方波时,输出也将仅为方波。当频率增加时,滤波器的输出看起来像三角波。如果增加频率,那么输出信号的幅度就会减小。
众所周知,三角波是由于电容器的作用而产生的,或者只是电容器的充电和放电模式导致了三角波。
低通滤波器的应用
主要用途是避免整流器输出中的交流纹波。
低通滤波器用于音频放大器电路。
通过使用这种无源低通滤波器,可以直接将高频噪声降低到立体声系统中的小干扰模式。
作为积分器可以用作波形整形和波形生成电路,因为可以轻松地将一种类型的电信号转换为另一种形式。
用于解调器电路,以从调制信号中提取所需参数。
-
低通滤波器截止频率计算公式_作用和用途2023-02-16 34114
-
低通滤波器(LPF)的定义及应用2022-04-14 43642
-
滤波电路(上),无源滤波器2022-01-11 1995
-
无源滤波器的相关资料推荐2022-01-03 2532
-
LC滤波器元件参数的计算公式及电路分析2021-06-22 5664
-
一文详解低通滤波器2020-12-14 25221
-
无源高通滤波器电路频率和相移计算公式摘要2019-06-27 40712
-
求教如何计算低通滤波器频率?2019-02-27 7630
-
求Sigmadsp的高阶滤波器计算公式2019-01-23 2830
-
RC无源低通滤波器设计问题?2019-01-08 4055
-
求 该无源带阻滤波器 各元件值计算公式2013-08-19 4590
-
无源带通滤波器电路,有源带通滤波器原理图2010-02-26 9378
-
无源低通滤波器电路,有源低通滤波器原理图2008-09-24 23348
全部0条评论

快来发表一下你的评论吧 !

