由串联电感器和并联电容器组成的结构介绍

在本文中，您会发现重点关注串联电感器，其中介绍了由串联电感器和并联电容器组成的梯形低通滤波器结构。

对于没有互通量耦合的串联电感，其电气效应类似于串联电阻，各个电感值简单地相加。

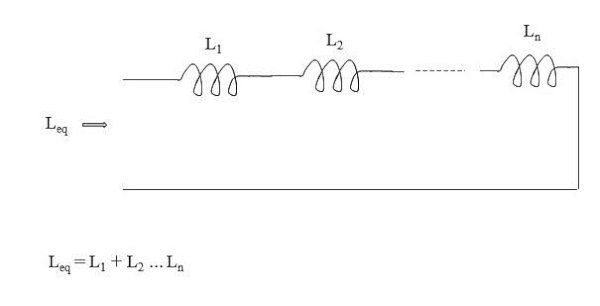
图 1. 串联电感的等效电感。图片由 Blaine Geddes 提供

推导

串联电感的等效电感很容易从第一原理（基本电路理论）推导出来，如图 2 所示。电感的特点是其两端产生的电压是其自感和流过它的电流的变化。由于公共电流流过该串联电路的所有元件，因此所有串联元件的电流变化率相同。共同的 di/dt 项抵消，导致等效电感是各个电感的总和。

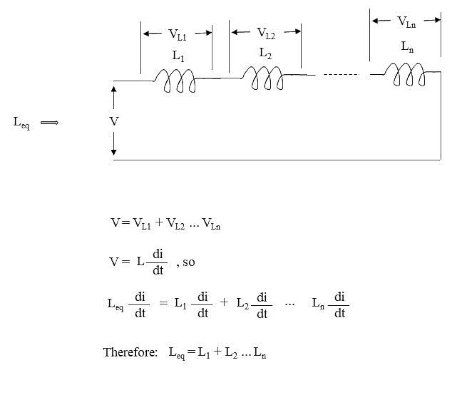
图 2. 串联电感等效电感的推导。图片由 Blaine Geddes 提供

LR电路的时间常数

在这篇 EE Power文章中，展示了图 3 的基本示例电路，其微分方程的解被发现为：

i=VR−VRe−RtLi=VR−VRe−RtL［1］

在时间 t=0 时，开关闭合，但 i = 0，因为电感器看起来像一个无限阻抗，以响应理想化的电流瞬时增加。由于理想电感器在零频率下没有阻抗，因此电流根据指数函数斜升以在直流电路的 V/R 值处达到稳定状态。方程［1］的微分方程满足这些边界条件。

表征基本 RL 或 RC 电路的常用参数是其时间常数，其定义为某个量达到其最终值的 1/e 以内的值或最终值的约 63% 的时间。对于等式 ［1］，电流的指数上升如图 4 所示，时间常数为 L/R。

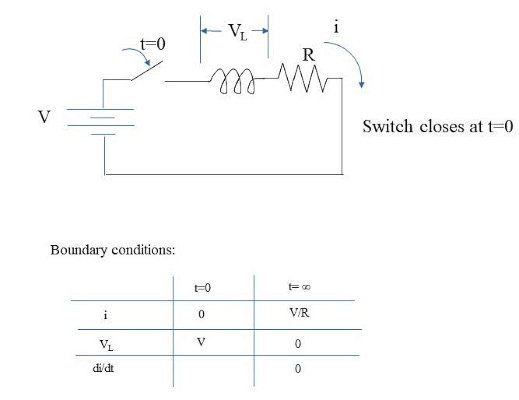
图 3. 带有串联电阻的电感器的直流瞬态分析。图片由 Blaine Geddes 提供

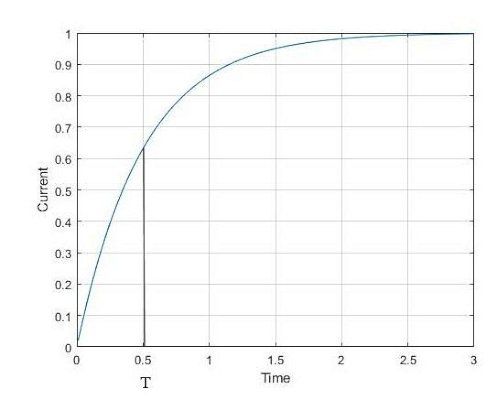
图 4. 等式 1 针对 V=2、R=2、L=1 绘制。时间常数为 L/R = 0.5。图片由 Blaine Geddes 提供

串联电感的应用

串联电感最常用于限制浪涌电流，例如电机启动的浪涌电流，以抑制高频信号，例如，抑制高频开关信号泄漏到电源轨上，或用作扼流圈限制来自整流交流电的直流电源的纹波。电感器还用于调谐电路、集总元件滤波器设计和阻抗匹配，以消除离散频率下的容抗。

电感器是一种有效的电流浪涌抑制器，因为它会在其两端产生一个电压，该电压与流过它的电流变化率成正比。因此，电流的瞬时变化与趋于无穷大的反电动势相反。电感器的理想模型是它代表电流瞬时变化的开路。在现实世界中，零时间间隔内什么都没有发生，所以即使是理想的电感器也不能在实际电路中产生无限大的电压，但如果突然中断通过电感器的大稳态电流，它可以产生非常高的电压。

过滤器

电感器和电容器可以组合形成一个基本滤波器。滤波器在整个电气工程中都很重要，并且大量用于通信电路，尤其是无线电。尽管随着通信电子设备越来越多地转向数字领域，模拟集总元件滤波器的重要性正在减弱，但模拟滤波器仍然很重要。滤波器还用于音频电路、控制系统和电源，用于过滤纹波和谐波。

一个简单的两元件低通滤波器及其传递函数的推导如图 5 所示。交换电感器和电容器的位置会产生高通响应。

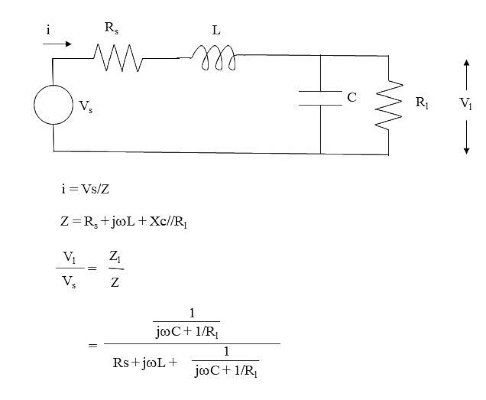
图 5. 两元件 LC 低通滤波器及其传递函数。图片由 Blaine Geddes 提供

绘制图 5 的电压传递函数与频率的关系图可得到图 6 的代表性图，其中 R、L 和 C 均设置为 1。生成该图的代码如下所示：

C=1；

Rl=1；

Rs=1；

L=1；

j=sqrt（-1）;

f=0.01:0.01:1；

Zl = 1./（j.*2.*pi.*f.*C + 1./Rl）;

Z = Rs + j.*2.*pi.*f.*L + Zl；

vl_vs = 20.*log10（abs（Zl./Z））+6;

情节（f，vl_vs）；

网格

xlabel（‘频率 （Hz）’）

ylabel（‘幅度响应（dB）’）

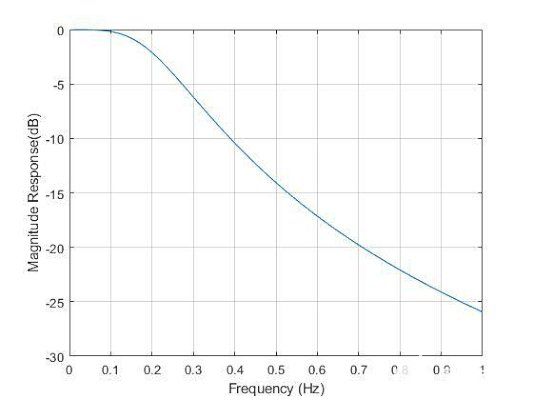
图 6. 图 5 的二元低通滤波器传递函数的幅度响应。图片由 Blaine Geddes 提供

具有串联电感器和并联电容器的基本两元件低通 LC 滤波器的概念可以扩展到图 7 的标准梯形结构。

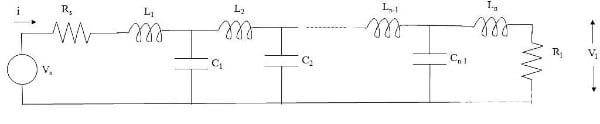
图 7. 低通 LC 梯形网络。图片由 Blaine Geddes 提供

分析集总元素梯形网络原则上很简单，但是对于多个元素，代数很快就会变得笨拙。除了几个元素之外，手动计算将变得不切实际，但基本代数计算简单且易于编程。上面显示的基本 MATLAB 代码可以很容易地扩展，以绘制更大梯形结构的响应。MATLAB 等数学软件可以通过隐式完成极坐标到矩形的转换来处理复数，从而简化了代码。合成梯形结构以产生特定响应在数学上涉及更多，并且远远超出了本文的范围，但滤波器对于电气工程来说是如此的基础，以至于该主题已经通过关于该主题的整篇文章进行了很好的研究。

对于图 7 的梯形结构，通常实现两种标准滤波器类型。这些被称为巴特沃斯和切比雪夫（或切比雪夫）滤波器。巴特沃斯滤波器响应的特点是通带响应基本平坦，但在通带上限处有一些衰减。Chebyschev 滤波器的特点是滚降比 Butterworth 滤波器更陡峭，但其代价是通带中的纹波，纹波幅度取决于所选的组件值。随着频率的增加，两种滤波器类型都提供单调增加的衰减。

滤波器表可用于滤波器设计，其中针对给定滤波器阶数和最大通带衰减选择列出归一化组件值。通带中的最大衰减位于巴特沃斯滤波器的上通带边缘，并且在切比雪夫滤波器的通带中表现为波纹。这样的一组表格在参考文献 1 中公布。元件值被归一化为一些源电阻和截止频率。对于参考表 1，这是 1 Hz 和 1 ohm。任何其他截止频率 （F ref ） 和源电阻 （R ref ） 的分量值通过缩放获得，其中：

L参考= R参考/2πF参考

Cref = 1/（2πF参考 R参考）

然后将每个列表组件值乘以 L ref 或 C ref 以获得各自的实际 L 和 C 值。

通过交换梯形结构中的电感器和电容器，可以将低通滤波器的列表值用于具有反向频率响应的等效高通滤波器。

第三种标准滤波器响应是椭圆滤波器的响应。与 Chebyshev 和 Butterworth 低通滤波器随着频率的增加而单调增加的衰减行为不同，椭圆滤波器的特征在于阻带衰减本底，在通带和阻带中都有纹波。椭圆滤波器的优点是它为给定的滤波器阶数提供最陡峭的滚降。代价是一个更复杂的滤波器结构，其中图 7 的基本低通阶梯被修改为图 8 或图 9 的。与切比雪夫和巴特沃斯滤波器一样，将参考低通椭圆滤波器转换为等效高通滤波器需要互换L 和 C 分量。

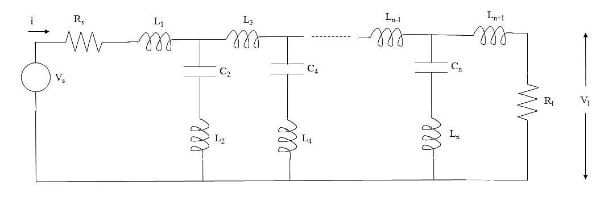
图 8. 用于实现椭圆响应的低通集总元件滤波器结构。图片由 Blaine Geddes 提供

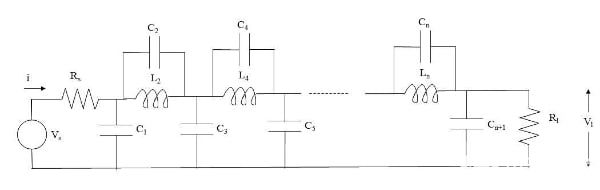
图 9. 用于实现椭圆响应的替代低通集总元件滤波器结构。图片由 Blaine Geddes 提供

对于任何滤波器设计，元件灵敏度分析都是一项重要的工作，以确保滤波器响应不会受到元件容差的过度影响。在高频下，组件寄生效应和轨道长度变得显着。如这篇 EE Power文章中所述，片式电感器在某些频率下会变成电容器。　　

      审核编辑：彭静