三相分支电路和馈线中的电压降计算介绍

三相系统在大型住宅区和商业和工业设施中最常见。三相系统在固定功率损耗下传输电力比单相系统更经济，这主要是因为减少了 I²R 损耗和导体中的电压降。本文讨论了计算三相系统中电压降的方法。

在三相系统中使用单相电压降公式和表格

减少三相系统中的 I²R 损耗和电压降允许使用更小的导体，从而减少所需的铜或铝的重量。

用于计算单相系统中电压降的公式和表格可以通过乘以因子在三相系统中使用。对这些因素的阐述需要回顾一些三阶段的基础知识。

平衡三相系统中的电压

公用发电厂中的同步发电机产生大部分通过作为三相电路运行的线路传输和分配的电力。

这些发生器产生三个正弦电压，它们之间具有相等的中方根 （RMS） 幅度和 120 电度的相移。由于电压是正弦的，因此它们的表示使用相量。

系统是平衡的，因为它们具有相等的 RMS 幅度。在正常运行条件下没有不平衡的发电机。

三个生成的电压可以以星形配置或三角形配置连接。Y 形连接在公用发电机中是典型的。图 1 显示了这两种格式。

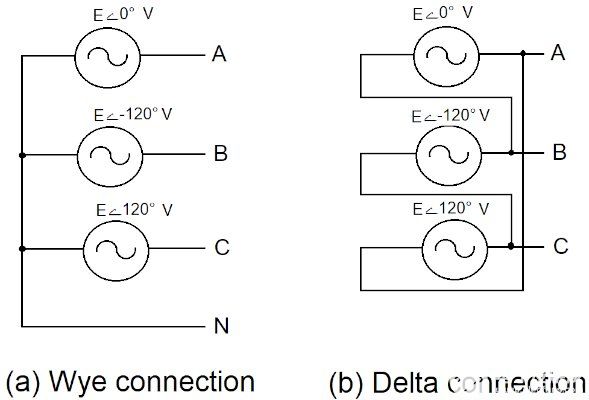
图 1.平衡三相电压源 Y 形和三角形连接。图片由 Lorenzo Mari 提供

Wye 连接

在 Y 形连接（图 1a）中，三个源端子形成一个公共节点，标记为中性线 （N）。

线对中性线的系统电压或相电压等于各个电源电压

V AN = E 00°

\［V_{BN} = Eے-120° V\］

\［V_{CN}= Eے120° V\］

为了确定线间电压或线电压，我们应用基尔霍夫电压定律 （KVL）

\［V_{AB} = V_{AN} – V_{BN} = Eے0° - Eے-120° = √3Eے30° V\］

\［V_{BC} = V_{BN} – V_{CN} = Eے-120° - Eے120° = √3Eے270° V\］

\［V_{CA} = V_{CN} – V_{AN} = Eے120° - Eے0° = √3Eے150° V\］

用 V L表示线电压的大小，用 V P表示相电压，我们有

V L = √3 V P

在 Y 形连接中，线电压幅度是相电压的 √3 倍。线电压和相电压之间存在相移。

三角洲连接

我们通过串联三个源来获得三角形连接（图 1b）。发电机中性点不存在，因为三个源没有共同点。例如，除了线对地电容（本分析未涵盖）外，不存在线对中性线电压。

在三角形连接中，线电压等于各个相电压，如下所示

\［V_{AB} = Eے0° V\］

\［V_{BC} = Eے-120° V\］

\［V_{CA} = Eے120° V\］

然后

V L = V P

平衡三相负载中的电流

图 2 显示了连接到 A、B 和 C 相的发电机的三个单相负载。

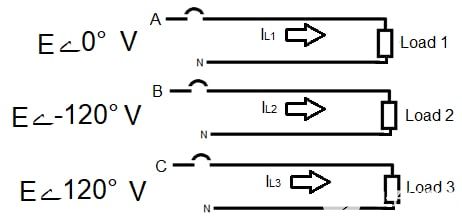
图 2.连接到发电机的单相负载。图片由 Lorenzo Mari 提供

三个单相电路具有电流 IL1、IL2 和 IL3，从电源流向负载并返回电源 - 假设星形连接的发电机绕组可连接中性点。每个中性线将承载电流，并且将应用单相电压降公式。

与源类似，三个单相负载可以以星形或三角形配置连接（图 3）。

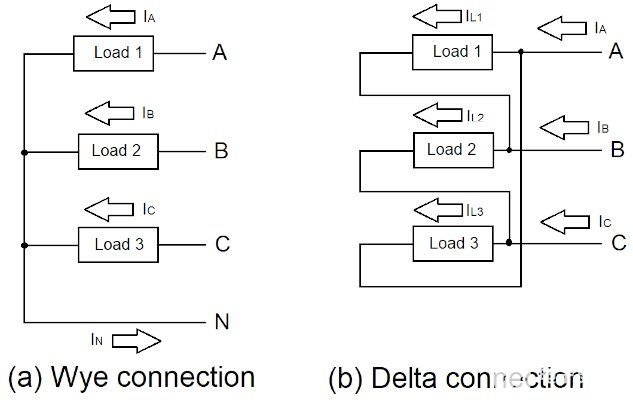
图 3.三相负载 Y 形和三角形连接。图片由 Lorenzo Mari 提供

星形连接

图 3a 显示了以星形连接的三个负载。术语 wye-wye 意味着源和负载是星形连接的。

施加到负载的电压等于源相电压。

在平衡系统中，三个阻抗相等。假设负载阻抗 Z 1 = Z 2 = Z 3 = Z P 0θ，欧姆定律给出以下相电流

\［I_{A} = V_{AN}/Z_{P} ےθ = Eے0°/Z_{P} ےθ A\］

\［I_{B} = V_{BN}/Z_{P} ےθ = E-120°/Z_{P} ےθ A\］

\［I_{C} = V_{CN}/Z_{P} ےθ = V_{CN} = Eے120°/Z_{P} ےθ A\］

三相电流大小相同，相移120°。

在星形连接的每一相中，线电流在幅度和相位上等于相电流。用 IL 表示线电流的大小，用 IP 表示相电流，我们有

我L = 我P = 我

应用基尔霍夫现行定律 （KCL）

我N = 我A + 我B + 我C = 0

在 Y 形连接的平衡三相系统中，中性线电流为零。由于在此对称电路中中性线不承载电流，因此可以忽略建立三相三线系统——尽管它在物理上是四线系统。

在我们关于电压降的讨论中，必须让电路在平衡条件下运行。因此，只有一根导体为每个负载供电，产生的电压降仅为不平衡条件下的一半——相位和中性线承载电流。

Wye-delta 连接

图 3b 显示了以三角形连接的三个平衡负载。施加到负载的电压等于源线电压。具有三角形连接负载的系统是三线制的，因为没有中性线连接。

根据源连接（星形或三角形连接），系统为星形或三角洲连接。Delta 连接的源是非典型的，因此我们将采用 Y 型连接的源。

假设负载阻抗 Z 1 = Z 2 = Z 3 = Z P 0θ，相电流为

\［I_{L1} = V_{AB}/ Z_{P} ےθ = √3E30°/Z_{P} ےθ A\］

\［I_{L2} = V_{BC}/ Z_{P} ےθ = √3E270°/Z_{P} ےθ A\］

\［I_{L3} = V_{CA}/ Z_{P} ےθ = √3E150°/Z_{P} ےθ A\］

具有三个相似的阻抗，这是一个具有相等相电流幅度的平衡负载，位移 120°。

应用 KCL 确定线路电流 I A、 I B和 I C

我A = 我L1 – 我L3

I B = I L2 – I L1

我C = 我L3 - 我L2

经过一些计算，我们得到

\［I_{A} = √3 I_{L1}30°A\］

\［I_{B} = √3 I_{L2}ے-30° A\］

\［I_{C} = √3 I_{L3}3-30° A\］

然后

I L = √3 I P

我们得出结论，线电流幅度等于相电流幅度的 √3 倍，假设正序，线电流滞后相电流 30°。

倍增因素

回忆一下计算单相电路中近似电压降的典型公式

VD = 2 x K x I L x L / A

在哪里

VD = 电压降

K = 导体电阻率

I L = 线电流（I L = I P在单相电路中）

A = 导体的横截面积

L = 从源到负载的距离

常数 2 考虑从负载到源的返回导体

寻找乘数的标准是

一个。常数 2 应该被删除，因为在三角形连接负载和平衡 Y 形连接负载中没有返回导体（中性线）——它们是三线电路。

湾。在三角形连接的负载中 I L = √3 I P。将公式中的I L代入√3 I P。VD 基于 V L，系数为 √3/2 = 0.866。

C。在星形连接负载中，V L = √3 V P。

c1。VD 基于 V L，将 VD 除以 √3，系数为 √3/2 = 0.866。

c2。对于基于 V P的 VD ，该因子为 ½ = 0.5。

总而言之，在三相系统中，如果使用线电压，则将单相结果乘以 0.866，如果使用相电压，则乘以 0.5。

示例 1

图 4 显示了一个为三角形连接的低电感负载供电的分支电路。使用以下铝单相公式计算三相电压降。

VD = 2 x 17.35 Ω CM/ft x I L （A） x L（ft） /CM

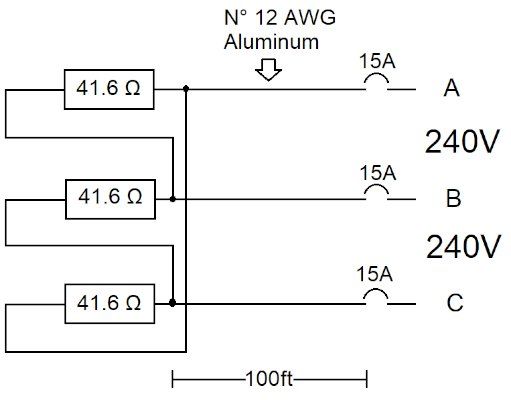
图 4.平衡的三相三角形连接负载。图片由 Lorenzo Mari 提供

I P = 240 V/41.6 Ω = 5.77 A

I L = √3 I P = 10 A

NEC 表 8 显示导体尺寸 N° 12 AWG 的 6 530 圆密耳。

VD = （2 x 17.35 Ω CM/ft x 10 A x 100 ft / 6 530） x 0.866 = 4.6 V

示例 2

图 5 显示了一个为星形连接的低电感负载供电的分支电路。根据 V P计算电压降不高于 1% 的铜线尺寸。对铜使用以下单相公式

CM = 2 x 10.895 Ω CM/ft x I（A） x L（ft） /VD（V）

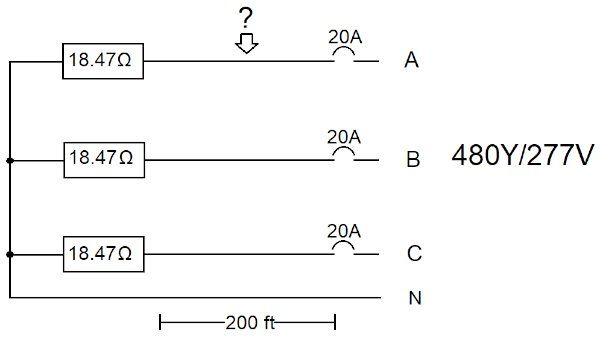
图 5.平衡的三相星形连接负载。图片由 Lorenzo Mari 提供

I = 277 V/18.47 Ω = 15 A

VD = 0.01 x 277 V = 2.77 V

CM = （2 x 10.895 Ω CM/ft x 15 A x 200 ft / 2.77 V） x 0.5 = 11 800

NEC 表 8 显示 N° 10 AWG 为 10 830 CM，N° 8 AWG 为 16 510。使用 N° 8 AWG。

示例 3

对基于 V L的不高于 1% 的电压降重复示例 2 。

I = 277 V/18.47 Ω = 15 A

VD = 0.01 x 480 V = 4.8 V

CM = （2 x 10.895 Ω CM/ft x 15 A x 200 ft / 4.8 V） x 0.866 = 11 800

使用 N° 8 AWG。

计算电压降的比例法

以下表达式有助于计算由于沿导体的电压降引起的电压降和相移

V R = V S x Z L /Z S

在哪里

V R = 负载相电压

V S = 源相电压

Z L = 负载阻抗

Z S = 系统阻抗，包括 Z L

所有量相表示

电压降的大小为

ƖVDƖ = ƖV SƖ – ƖV RƖ

示例 4

图 6 显示了向功率因数不同于 100% 的设备供电的电源。

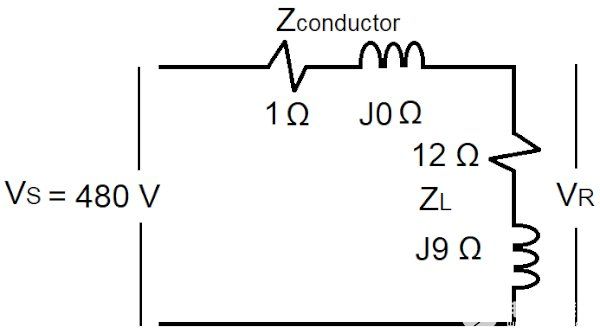
图 6.为设备供电的源。图片由 Lorenzo Mari 提供

一个。以极坐标形式计算 Z L。

极坐标格式为

ƖZ LƖêθ _

ƖZ LƖ = √（12² + 9²） = 15 Ω

θ = tan¯¹ 9/12 = tan¯¹ 0.75 = 36.9°

\［Z_{L} = 15 36.9° Ω\］

湾。以矩形和极坐标形式计算 Z S。

矩形的格式是

Z S = R + jX

Z S = 1 + j0 + 12 + j9 = 13 + j9 Ω

ƖZ SƖ = √（13² + 9²） = 15.81 Ω

θ = tan¯¹ 9/13 = tan¯¹ 0.69 = 34.7°

\［Z_{S} = 15.81ے 34.7° Ω\］

C。计算负载上的电压。选择 VS 作为参考。

\［V_{R} = 480 x 0° \times 15 x 36.9°/15.81 x 34.7° = 455.4 x 2.2° V\］

d。以伏特和百分比计算电压降幅度。

ƖVDƖ = 480 V – 455.4 V = 24.6 V

24.6 V/480 V x 100 = 5.13%

e. 导体引入的相移是多少？

2.2°

F。计算设备负载系数。

PF = cos θ = cos 36.9° = 0.8 = 80% 滞后

三相电路中使用的典型近似公式

只需要一相来确定在平衡条件下运行的三相系统中的电压降。图 7 的相量图显示了电源、负载和导体（闭合回路）的单相电压。

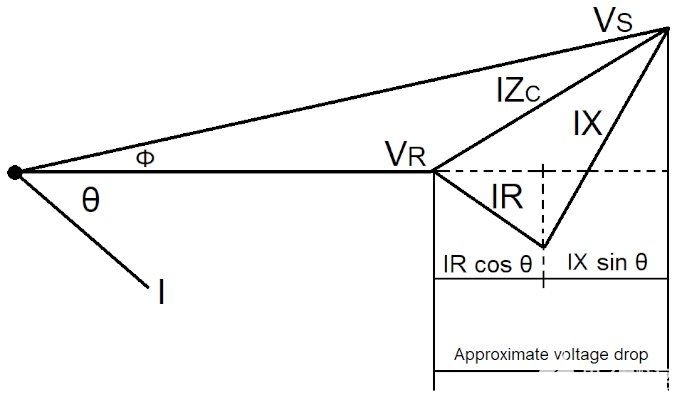
图 7.用于电压降计算的单相相量图。图片由 Lorenzo Mari 提供

实轴上的导体电压投影近似于电压降幅值。结果是

ƖVDƖ = I （R cos θ + X sin θ）

在哪里

ƖVDƖ = 线电压降幅度

I = 线路电流大小

R = 导体电阻

X = 导体电抗

θ = 负载角

cos θ = 负载功率因数

sin θ = 负载无功系数

随着角度 Φ 接近于零，公式误差减小——公式对于 Φ = 0 是精确的。实际上，角度 Φ 很小。

修改这个方程直接计算百分比电压降，我们得到

VD% = kVA （R cos θ + X 无 θ） /10 kV2

在哪里

VD% = 电压降百分比

kVA = 三相视在功率

kV = 线电压

请注意，kVA 和 kV 是三相值。

示例 5

一个。使用近似公式和示例 4 的结果，计算图 6 电路中的电压降幅值。

\［I = 480V0°/15.81？34.7° = 30.36？-34.7°A\］

线电流的大小 = 30.36 A

Z L角 = θ = 36.9°

R = 导体电阻 = 1 Ω

X = 导体电抗 = 0 Ω

cos θ = 负载功率因数 = 0.8

sin θ = 负载无功系数 = 0.6

ƖVDƖ = 30.36 x （1 x 0.8 + 0 x 0.6） = 24.29 V

湾。计算百分比电压降。

24.29 V/480 V x 100 = 5.06%

C。直接计算电压降百分比。

视在功率 = 30.36 A x 0.48 kV = 14.57 kVA

VD% = 14.57 （1 cos 36.9° + 0 sin 36.9°） /10 x 0.48² = 5.06%

例 6

三相地下电缆为平衡的感应负载（滞后功率因数）供电。系统数据如下

电缆阻抗 ZC = 0.0771 + j0.0724 Ω/相

负载阻抗 ZL = 13.75 + j10.31 = 17.19 36.86° Ω/相

源电压 4.16Y/2.4 kV

一个。使用比例法确定电压降。

V R = V S x Z L /Z S

\［Z_{S} = Z_{C} + Z_{L} = 0.0771 + 13.75 + j（0.0724 + 10.31） = 13.83 + j10.38 = 17.29

36.9° Ω/相\］

选择相电压作为参考

\［V_{S} = 2 400 0° V\］

\［V_{R} = 2 400 ε0° \乘以 17.19 ε36.86° / 17.29 ε36.9° = 2 385.4 ε-0.04°\］

\［ƖVDƖ = 2 400 V - 2 385.4 V = 14.6 V\］

\［14.6 V/2 400 V x 100 = 0.61%\］

湾。使用近似公式确定电压降。

ƖVDƖ = I （R cos θ + X sin θ）

Z L角 = θ = 36.86°

R = 导体电阻 = 0.0771 Ω

X = 导体电抗 = 0.0724 Ω

cos θ = 负载功率因数 = 0.8

sin θ = 负载无功系数 = 0.6

\［I = V_{S}/Z_{S} = 2 400 0° /17.29 36.9° = 138.72 ～-36.9° A\］

线电流的大小 = 138.72 A

ƖVDƖ = 138.72 （0.0771 x 0.8 + 0.0724 x 0.6） = 8.56 + 6.03 = 14.6 V

C。直接计算电压降百分比。

VD% = kVA （R cos θ + X 无 θ） /10 kV2

线电压 = V L = 4.16 kV

三相 kVA = √3 x V L x I = √3 x 4.16 kV x 138.72 A = 1 000 kVA

VD% = 1 000 （0.0771 x 0.8 + 0.0724 x 0.6） / 10 x 4.16² = 0.61%　　

      审核编辑：彭静