计算单相分支电路和馈线电压降的公式

适用于计算直流电压降的一些近似方法可能适用于负载小、相当短且导体间距较近的交流电路。这些方法忽略了线路电抗的影响。然而，它对结果的影响可能小于简单接线计算中遇到的其他因素。

圆形米尔

圆密耳 （CM） 是导体横截面积的量度。图 1 显示了圆形导体的实际横截面积 A = ΠD²/4 = 3.1416 x D²/4。

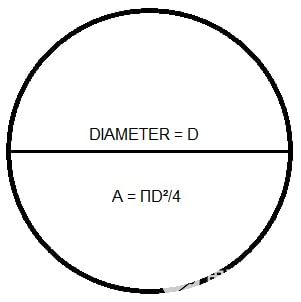
图 1.导体横截面。图片由 Lorenzo Mari 提供

找到圆形密耳的面积需要密耳的直径。

1 mil = 1/1 000 英寸 = 10ˉ³ 英寸 （in）

根据定义，直径 D = 1 mil 的导体的横截面积为 1 厘米。

如果 D = 1 mil，则 A = 1 CM = 3.1416 x D²/4 = 3.1416 x ¼ = 0.7854 平方密耳 （sq mils）

平方密耳 = 0.7854 x 厘米

厘米 = 1/0.7854 x 平方密耳 = 1.2732 x 平方密耳

选择 D = N mils（N = 任意正数）的导体。

A = 0.7854 x N² 平方密耳

厘米 = 1.2732 x 0.7854 x N² = N²

然后，任何导体的圆形密耳面积等于密耳平方的直径。

ACM = D²

以 mm² 为单位的面积是

Amm² = ΠD²/4 = 0.7854 x D²

其中 D = 直径，单位为 mm。

NEC 表 8

NEC 表 8 显示标准导体尺寸。它的导体尺寸从 18 到 4/0 AWG（美国线规）和从 250 到 2 000 kcmil、铜（未涂层和涂层）和铝。18 至 8 AWG 尺寸包括实心圆形和绞合导体。除其他数据外，表 8 以圆形密耳、mm² 和 in.² 为单位显示横截面积。

表 8 还包含 75°C 时的导体直流电阻。NEC 的电阻、电抗和阻抗值是线对中性线或欧姆对中性线。

示例 1。

求直径为 0.1285 英寸的实心导体的导体尺寸。

0.1285 英寸 = 1.285 亿

ACM = D² = 128.5² = 16 512

表 8 显示尺寸为 N° 8 AWG 的 CM = 16 510。

这个问题可以通过在表 8 的“总直径”列中查找 0.128 英寸的直径来解决。观察到绞合导体的总直径大于实心导体的总直径。

示例 2。

计算示例 1 中导体的横截面积，单位为 mm²。

D = 0.1285 英寸 x 25.4 毫米/英寸 = 3.264 毫米

Amm² = 0.7854 x D² = 0.7854 x 3.264² = 8.367 mm²

表 8 显示实心导体 N° 8 AWG 的面积为 8.367 mm²。

计算电压降的公式

计算单相电路中近似电压降的典型公式是

VD = 2 x ρ x I x L / A

在哪里：

A = 以 CM 或 mm² 为单位的导体横截面积。

ρ = 导线材料的电阻率，单位为 Ω CM/ft 或 Ω mm²/m。ρ 是 1 英尺长的导体、1 CM 的横截面积或 1 m 长的导体以及 1 mm² 的横截面积的电阻 - 回想一下 R = ρL/A。

I = 负载电流 （A）。

VD = 电压降 （V）。

L = 从源到负载的距离，以英尺或米为单位。

常数 2 考虑了从负载到源的返回导体。

要确定会产生特定电压降的导线尺寸，请将公式转置为

A = 2 x ρ x I x L / VD

一些参考文献将这些公式描述为

VD = 2 x K x I x L / A

A = 2 x K x I x L / VD

式中 K 为导体电阻率。

英制和公制单位的电压降公式

商用硬拉铜线在 25°C 时的电阻率为 10.895 Ω CM/ft 或 0.018113 Ω mm²/m。

商用铝线在 25°C 时的电阻率为 17.345 Ω CM/ft 或 0.028834 Ω mm²/m。

由于分子运动增强，铜和铝的电阻随着温度的增加而增加，这一点至关重要。以下公式中的材料常数将随温度变化。

英制单位

2 x K = 2 x 10.895 Ω CM/ft = 21.79 Ω CM/ft

CM = 21.79 Ω CM/ft x I（A） x L（ft） / VD（V） 用于铜

2 x K = 2 x 17.345 Ω 厘米/英尺 = 34.69 Ω 厘米/英尺

CM = 34.69 Ω CM/ft x I（A） x L（ft） / VD（（V） 用于铝

要计算每个导体的 K，请根据 NEC 表 8 将圆形密耳乘以每英尺的电阻。

K = CM x Ω/ft = Ω CM/ft

表 1 显示了 K = 12.873 Ω CM/ft 的平均值，考虑到铜导体（75°C 时的直流电阻）。

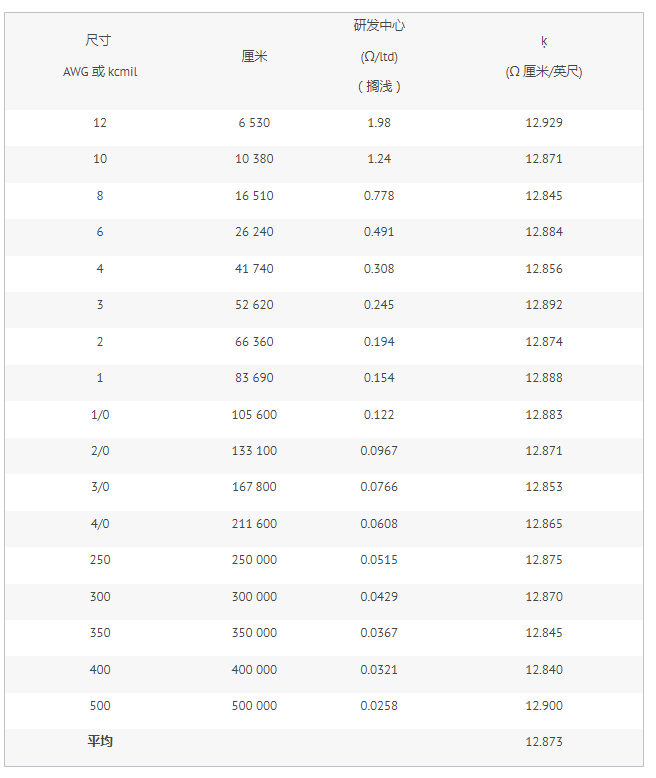
表 1.从 NEC 表 8 数据（铜导体）得出的 K 平均值。

使用 K 平均值的单相电路方程为

2 x K = 2 x 12.873 = 25.746

CM = 25.75 Ω CM/ft x I（A） x L（ft） / VD（V），铜在 75°C

表 2 显示了铝导体的 K = 21.182 Ω CM/ft 的平均值。

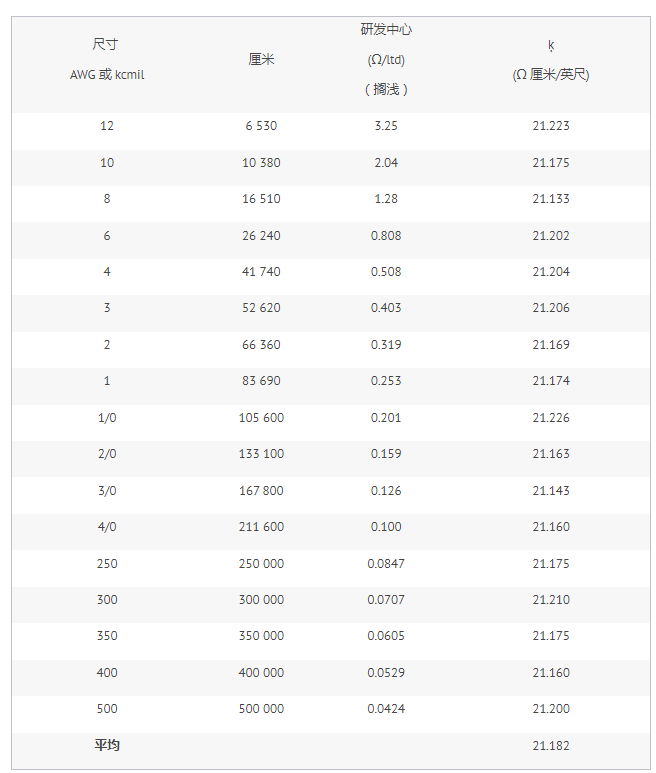
表 2.从 NEC 表 8 数据（铝导体）得出的 K 平均值。

使用 K 平均值的单相电路方程为

2 x K = 2 x 21.182 = 42.364

CM = 42.36 Ω CM/ft x I（A） x L（ft）/VD（V） 对于铝，在 75°C

公制单位

对单相电路执行类似的程序（在 25°C 时）会导致

2 x K = 2 x 0.018113 Ω mm²/m = 0.03623 Ω mm²/m

A（mm²） = 0.03623 Ω mm²/mx I（A） x L（m） / VD（V） 对于铜，以及

2 x K = 2 x 0.028834 Ω mm²/m = 0.05767 Ω mm²/m

A （mm²） = 0.05767 Ω mm²/mx I（A） x L（m） / VD（V） 用于铝

我们不计算 75°C 时铜的 K 平均值，而是仅计算 500 kcmil 导体的 K，数据来自 NEC 表 8。

K = 253 mm² x 0.0845 Ω/km /1 000 = 0.021379 Ω mm²/m

2 x K = 2 x 0.021379 Ω mm²/m = 0.04276 Ω mm²/m

A = 0.04276 Ω mm²/mx I（A） x L（m） / VD（V） 用于铜

使用 NEC 表 8 中的数据计算 500 kcmil 铝导体在 75°C 下的 K。

K = 253 mm² x 0.1391 Ω/km/1 000 = 0.035192 Ω mm²/m

2 x K = 2 x 0.035 Ω mm²/m = 0.07038 Ω mm²/m

A = 0.07038 Ω mm²/mx I（A） x L（m） / VD（V） 用于铝

共享英制和公制单位的公式

以下公式结合了单相电路中 25°C 时铜导体的英制和公制单位。

厘米 = 70.86 x I（A） x L（m） / VD（V）

这些近似公式适用于具有高功率因数（最好为 100%）的直流和交流电路，这在住宅电气装置中通常是这种情况。

商业和工业电气装置中的电压降计算通常需要使用阻抗而不是电阻的公式。将公式应用于具有低功率因数负载和显着线路电抗的交流电路可能会导致严重错误。

示例 3。

在图2的电路中

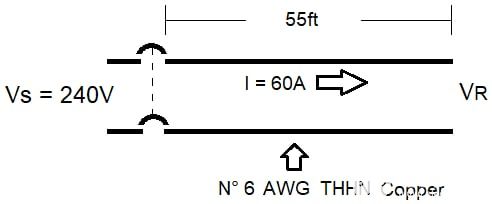
图 2. 240V、2 线、单相电路。图片由 Lorenzo Mari 提供

一个。使用英制单位在 25°C 时以伏特和百分比计算 VD。

NEC 表 8 显示了 26 240 圆密耳的导体 N° 6 AWG。

VD = 21.79 Ω 厘米/英尺 x 60 A x 55 英尺/26 240 = 2.74 V

VD = （2.74V/240V） * 100 = 1.14%

湾。求接收端电压 VR。

VR = Vs – VD

VR = 240 V – 2.74 V = 237.26 V

例 4。

在 25°C 下使用公制单位重复示例 1。

一个。

NEC 表 8 显示 13.30 mm² 的导体 N° 6 AWG。

50 英尺 x 0.3048 米/英尺 = 16.764 米

VD= 0.03623 Ω mm²/mx 60 A x 16.764 m / 13.30 mm² = 2.74 V。

VD = （2.74V/240V） * 100 = 1.14%

湾。

VR = Vs – VD

VR = 240 V – 2.74 V = 237.26 V

例 5。

使用英制/公制公式计算示例 1 中的 VD。

VD = 70.86 x 60A x 16.764 m/26 240 = 2.72 V。

电压降表

无需每次都应用电压降公式。虽然有很多关于这个主题的软件，但手头有一些表格来快速估算总是很实用的。

了解表格的基础至关重要，例如使用的公式、单相或多相、电线数量、导体材料、交流或直流、磁性或非磁性导管、环境温度、功率因数和频率。

表 3 根据公式显示了铜导体的电压降

VD（V） = 25.75 Ω CM/ft x I（A） x L（ft） / CM，对于 75°C 的铜

此表使用安培英尺法。乘积 I（A） x L（ft） 变为常数，如下所示：以相同的比例增加电流和减少距离，反之亦然，保持 VD 不变。

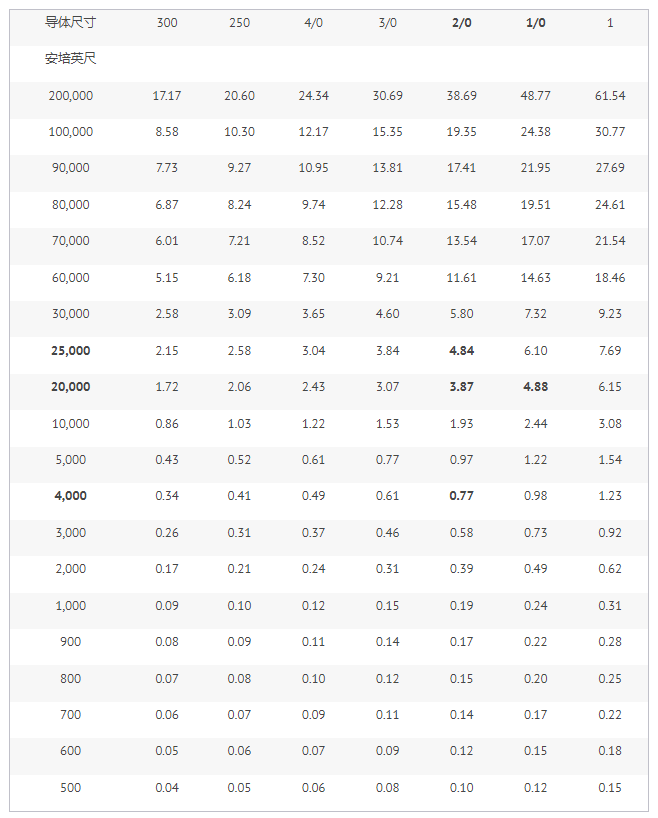
表 3.非磁性导管中铜导体的电压降。单相、2 线和 3 线、100% 功率因数、60Hz。

安培英尺 = I（A） x L（ft）

VD（V） = 25.75 Ω x 安培英尺/厘米

例 6。

图 3 显示了一个 120/240V、3 线、单相馈线，它为具有 23 kW 平衡负载的照明面板供电。使用表 3，如果运行长度为 250 英尺，计算最大线间电压降 2% 所需的铜导体尺寸。

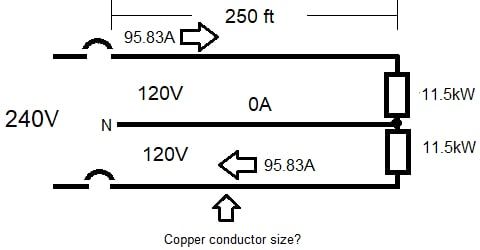
图 3.为照明负载供电的 120/240 V、3 线、单相电路。图片由 Lorenzo Mari 提供

I = 23 千瓦/240 伏 = 95.83 安

L = 250 英尺

95.83 A x 250 英尺 = 23，958 A-ft，例如 24，000 A-ft

允许的最大 VD = 240 x 0.02 = 4.8 V

表 3 显示在 20，000 A-ft 线和尺寸 1/0 列的交叉处的 VD = 4.88 V，高于所需的 VD。

VD = 4.84 V 在 25，000 A-ft 线和尺寸 2/0 列的交叉处，余量为 1，000 A-ft。

在 3.87 V （20，000 A-ft） 和 4.84 V （25，000 A-ft） 之间插值，实际 VD = 4.64 V （24，000 A-ft） = 1.93%，低于所需的 VD。

使用尺寸 N° 2/0 的导线。

解决表 3 问题的另一种方法。

试穿 2/0 码

24，000 英尺 = 20，000 英尺 + 4，000 英尺

20，000 A-ft 时的 VD = 3.87 V

4，000 A-ft 时的 VD = 0.77 V

总 VD = 3.87 V + 0.77 V = 4.64 V = 1.93%

使用尺寸 N° 2/0 的导线。

有使用安培计方法的类似表格。

概括

CM 定义了横截面积。一圆密尔是直径为1密尔的圆的面积。

导体横截面积的另一种表达方式是平方毫米 （mm²）。

NEC 表 8 提供了大量的导体数据。

几个公式允许在简单电路中以近似结果计算电压降。这些公式在线路电抗可忽略不计和高功率因数负载的直流电路和交流电路中很有帮助。

在大多数情况下，没有必要使用公式来确定电线尺寸。有许多表格可用于快速计算。了解用于避免计算错误的表格的基础至关重要。　　

      审核编辑：彭静