

声光偏转器的工作原理及性能指标
电子说
描述
声光偏转器及其应用(一)
声光偏转器原理
声光偏转器是利用声光效应而设计的功能器件,在光束控制、光信号处理、光计算、光通信等领域得到广泛的应用。
声光器件是福晶科技的核心器件产品,本期福晶小课堂推出《声光偏转器连载栏目》,连续三天为您系统详尽地介绍关于声光偏转器的基础原理、应用领域、产品系列等相关知识和发展方向。
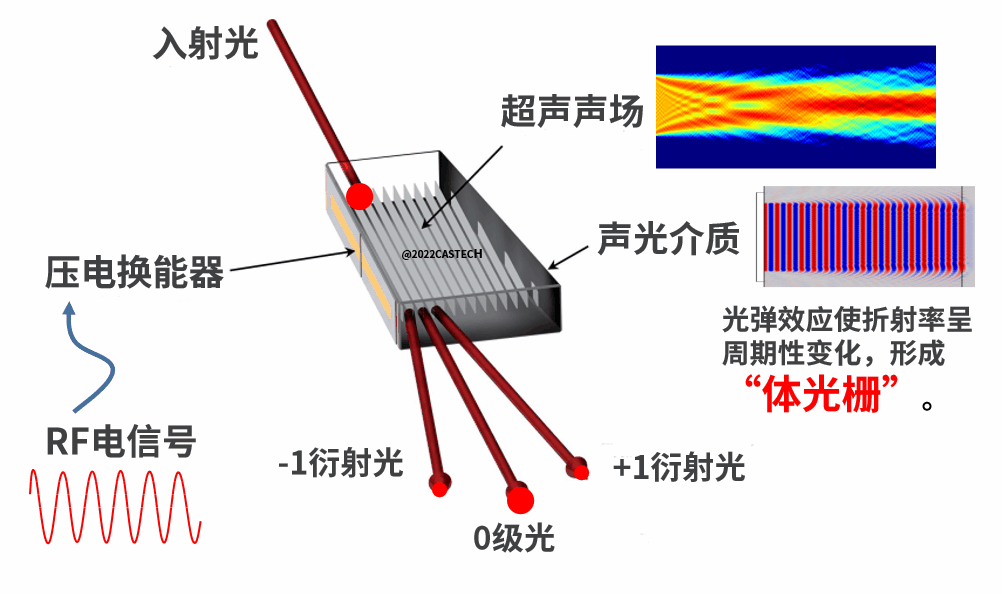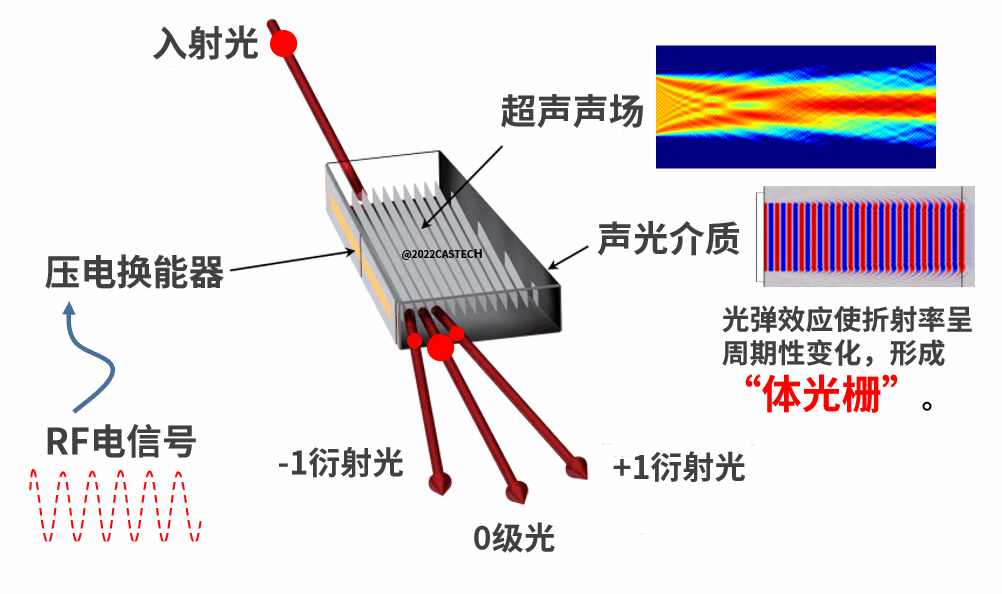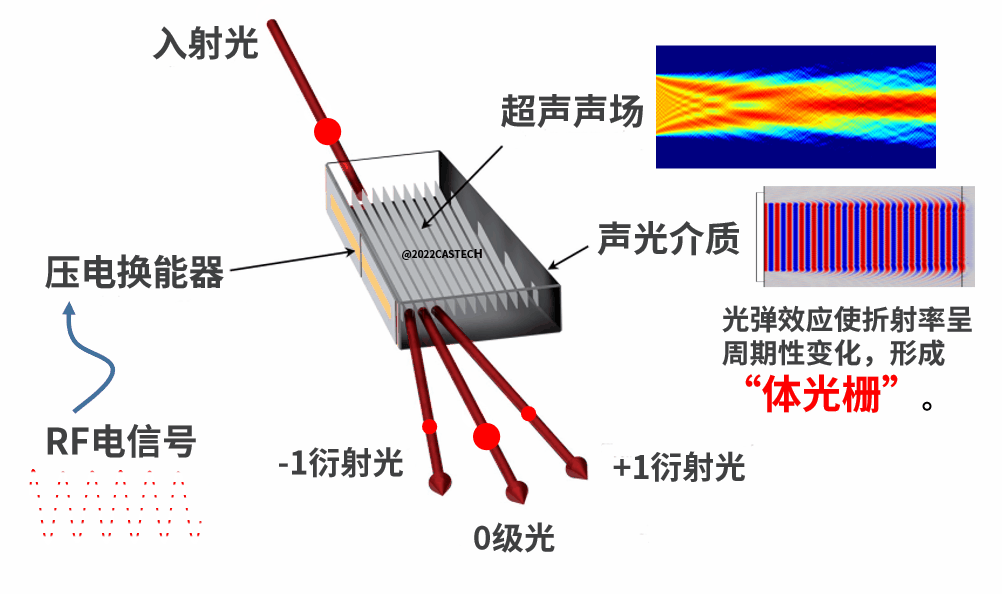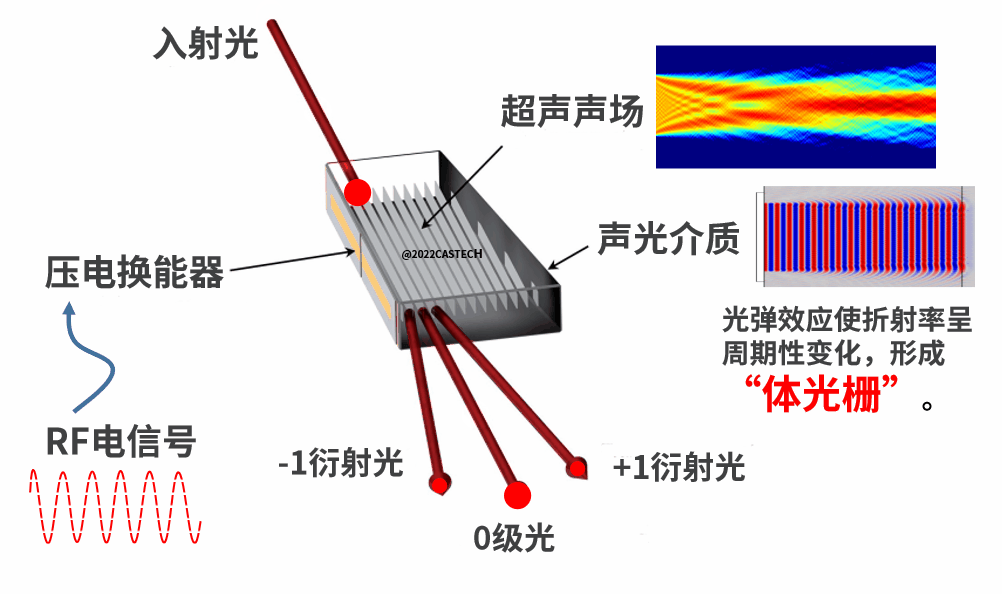
图1.1 声场作用示意图
在连载(一)中,我们首先来了解声光偏转器及其工作原理。
超声波在晶体中传播会使晶体折射率发生周期性变化,从而使入射光发生衍射的现象称为声光效应。声光偏转器(AODF)是基于声光效应原理而开发的器件,偏转角度可通过控制射频驱动器的频率来精确控制。与传统振镜扫描光束相比,声光偏转器具有超高扫描速度(扫描速度超过250KHz,而一般振镜扫描频率往往在KHz水平),宽光谱范围,高扫描分辨率,高光通量等优点。
声光效应
超声波在声光晶体中传播时,会导致晶体折射率的周期性变化,类似产生一个相位体光栅,入射光发生衍射,如图1.2所示。可通过改变超声场功率和频率的变化来有效控制衍射光的方向、强度和频率[1]。
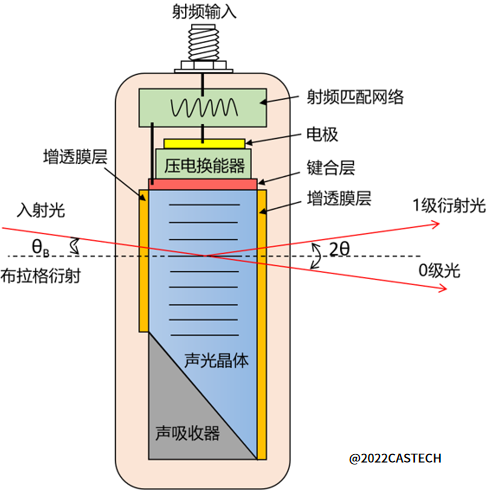
图1.2 声光效应原理图
声光效应最初在1922年被L.Brillouin所预言[2];美国科学家P.Debye和W.Sears通过实验验证了声光衍射的存在[3];随后由于激光的出现,从1966年到1976年,声光相互作用理论与声光器件的研究得到了迅速的发展,其中狄克逊的Dixon方程,W.R.Klein和B.D.Cook的声光耦合波方程I.C.chang的动量匹配和失配理论不断完善了人们对声光效应的认知[4]。
C.Raman和N.Nath用耦合波方程对声光衍射中的多级衍射光与一级衍射光的关系进行了解释,并且把声光作用方式分为布拉格(Bragg)衍射与拉曼-奈斯(Raman-Nath)衍射[5]。声光相互作用存在一个特征长度L0,拉曼-奈斯声光效应的相互作用区域比较短,L≤L0,声光晶体相当于一个平面光栅,对入射光方向要求不严格,如图1.3(a)所示,可以产生多级衍射光;布拉格声光效应的相互作用区域比较长,L≥2L0,整个晶体相当于是一个体光栅,对入射光方向要求很严格,只有满足布拉格条件的入射光才能产生衍射光,高级衍射光几乎被相互抵消,只剩下0级和±1级衍射光,见图1.3(b)。由于布拉格衍射具有极高的衍射效率,因此我们声光器件的设计与应用多使用布拉格衍射。
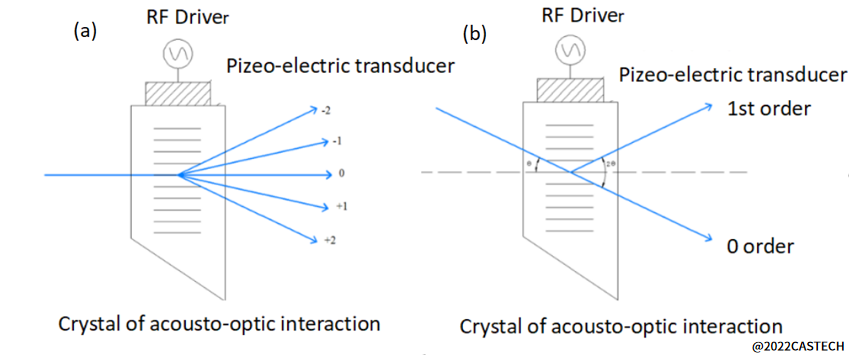
(a)拉曼-奈斯衍射 (b)布拉格衍射
图1.3声光作用方式
声光晶体
制作声光器件需要具有弹性系数大、介质均匀性好、声速小、超声衰减小、光透过范围宽、尺寸大等特性的声光晶体。目前主要使用的声光晶体有钼酸铅(PbMoO4)、二氧化碲(TeO2)、铌酸锂(LiNbO3)、石英(Quartz)和熔融石英(Fused Silica)等材料,这些材料具有衍射效率高与工作带宽大等特性,通过对工作模式的优化,可实现器件功能的优化设计。
声光偏转器工作原理
声光偏转器主要由声光介质和电声换能器组成,模型如图1.4所示,声光介质是声光相互作用的媒介,电声换能器也称超声波发生器,作用是将电功率转化为声功率,使得在介质中产生超声场。由于声波是一种弹性波,声波在介质中传播会产生弹性应变,这种现象称为弹光效应,弹性形变又会导致介质折射率发生变化。这种折射率的变化载有声波信息,效果相当于在介质上建立了折射率光栅,其间隔等于声波的波长。超声波频率随不同频率的接收信号改变时,光栅间隔也跟变化。在一定条件下,光束穿过折射率光栅时会发生布拉格衍射。电声换能器输入电压信号的变化可改变声波频率,控制不同角度的声波偏转。布拉格衍射时,理论上入射光束能量可以全部转化到衍射光束,衍射效率级高。
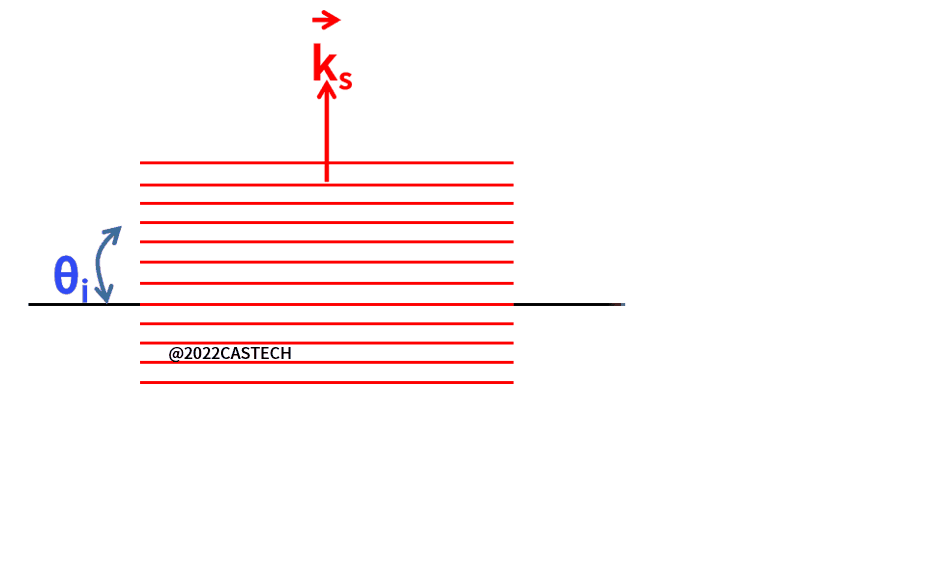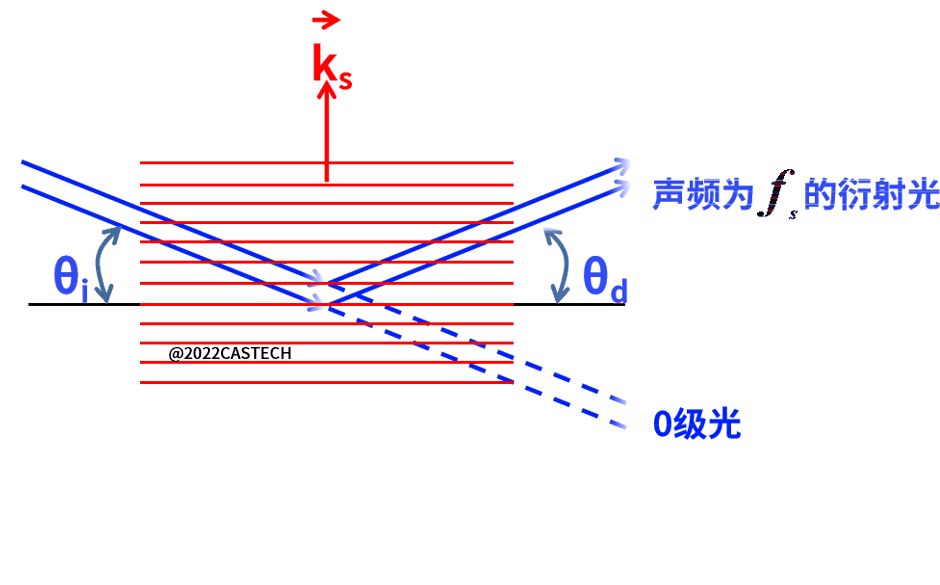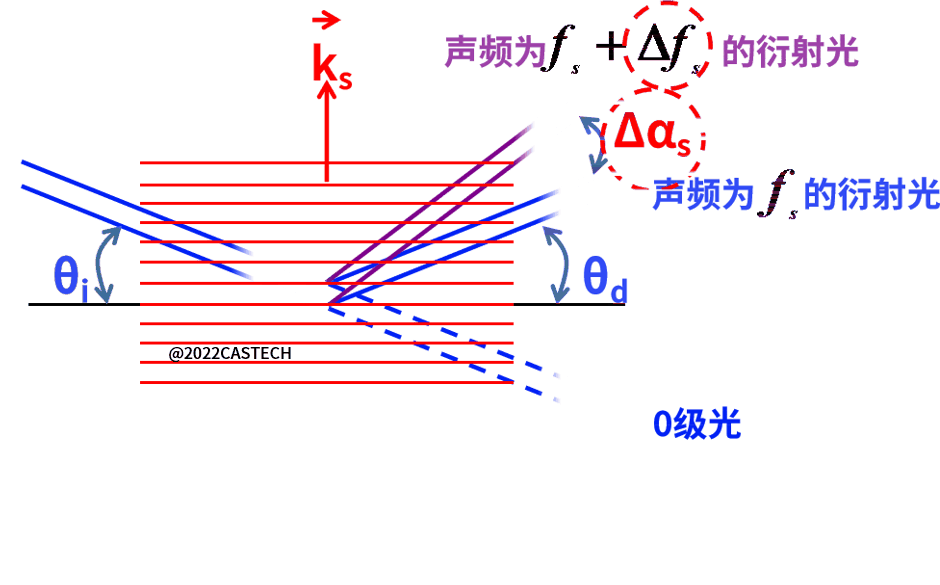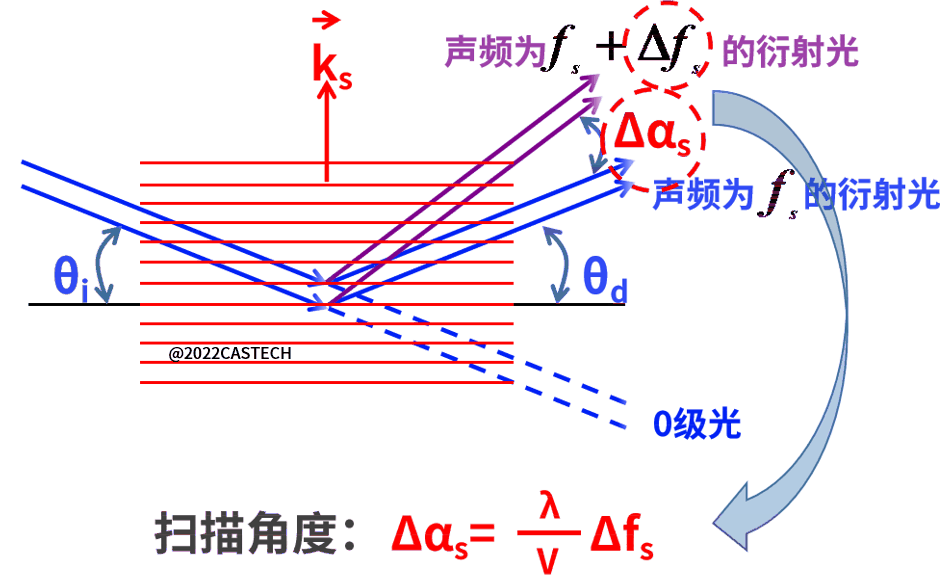
图1.4 声光偏转器原理示意图
由声光布拉格衍射理论可知,光束以θi角入射产生的衍射极角应满足布拉格条件:
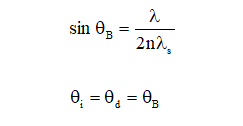
其中θi为入射角,θd为衍射角,θB为布拉格角。
布拉格衍射角一般很小,与光波长λ,声波长λs和晶体折射率n有关,可以写为:
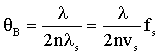
故衍射光与入射光夹角(偏转角)为布拉格角2倍,即:
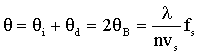
可知,声速vs确定,改变超声波频率fs,就可以改变偏转角θ,进而达到控制光束传播方向的目的,超声波频率改变Δfs引起光束偏转角的变化为:
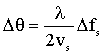
所以,当声光器件工作于布拉格模式时,衍射光束方向与超声波频率和入射光束有关,且偏转范围与Δfs成正比。
性能指标
声光偏转器的主要性能指标包括如下的衍射效率、可分辨点数、速度容积比、偏转时间、带宽等。
动量匹配的布拉格衍射下,一级衍射光衍射效率为:
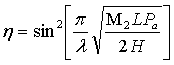
式中,L、H、Pa、M2分别为换能器的长度、宽度、超声波功率及声光优值,M2是描述声光晶体本身性质的常数,表达式为:
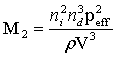
其中,ρ为晶体密度。ni和nd分别为入射光与衍射光折射率,Peff为有效声光系数。由衍射效率公式可知,参数合适时衍射效率可为1。
可分辨点数N决定声光偏转器件的容量,
定义为:
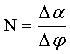
Δα为总扫描角,Δφ为光束本身发散角。
偏转时间等于渡越时间τ,τ定义为超声波通过激光束宽度w所用时间,
即:
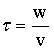
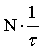
数值的大小是设计声光偏转器的重要指标,称为速度容积比,该指标只取决于器件的工作带宽Δf。
在声光相互作用过程中,超声波使入射光束在一定频率范围内实现布拉格衍射,该频率范围称为布拉格带宽。布拉格衍射需满足动量匹配条件Δk=0,θi与f的关系由Dixon方程确定,每一个入射角θi对应唯一的超声频率f。因此在超声频率内选择合适方向的超声波,使入射角满足Dixon方程,就是主要考虑的布拉格带宽问题。设频带的高端频率为fH,低端频率fL,二者满足
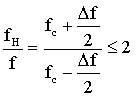
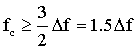
由上式可以看出,确定了器件的工作带宽即可确定器件的中心频率fc以及高、低端频率。定义非超声跟踪的声光互作用相对带宽为:
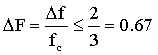
上式称为倍频程带宽,在声光器件优化设计上,相对带宽要小于或等于0.67。
伴随光电子技术的发展,声光器件以其优异的性能已在诸多领域得到广泛的应用。在下期的连载中我们将详细介绍声光偏转器的性能优势和应用领域。
审核编辑:汤梓红
-
LDO简介、工作原理及性能指标2022-09-21 31638
-
电性能指标测试2012-08-17 3242
-
任意波形发生器有哪些性能指标?2021-05-08 3022
-
频率响应法-- 频域性能指标和时域性能指标的关系2009-07-27 13560
-
传感器性能指标2009-11-07 3091
-
放大电路的性能指标2009-12-14 15261
-
比较器的性能指标/分类/应用2010-03-22 2052
-
检测系统的性能指标2011-03-13 1114
-
硬盘性能指标概述2012-05-03 5387
-
计算机cpu性能指标与作用2012-05-25 4569
-
常用集成稳压器型号与性能指标2016-03-21 1382
-
动态性能指标定义2016-12-30 1220
-
电缆性能指标测试方法2021-06-22 1234
-
声光偏转器的优势和应用2022-08-31 5823
-
瞬态响应的性能指标包括哪些2024-07-29 3148
全部0条评论

快来发表一下你的评论吧 !

