

影响材料弹性模量的因素
描述
1. 合金元素与钢材弹性模量的关系
原子间作用力决定于金属原子本身和晶格类型,故弹性模量也主要取决于金属原子本性与晶格类型。溶质元素虽可以改变合金的晶格常数,但对于常用金属材料而言,合金元素对其晶格常数的改变不大,因而对弹性模量影响小。合金钢和碳钢的弹性模量数值相当接近,差值不大于12%[10]。
2. 热处理对弹性模量的影响
热处理对弹性模量的影响不大,如晶粒大小对弹性模量无影响;第二相大小和分布对弹性模量影响也很小;淬火后弹性模量虽有所下降,但回火后又恢复到退火前的状态值[10]。但是,弹簧钢 (60Si2MnA) 在经过热处理(淬火+回火)后,弹性模量变化不大,而不同的温度回火后,切变模量变化较明显,具体可参见文献[11,12]。设计中若对此不予以考虑,可能会造成一定误差。
对于60Si2MnA材料热处理虽然对E的影响很小,但是G却有明显变化,根据剪切模量、弹性模量及泊松比的关系:G=E/(2(1+υ)),可以得出是热处理会影响υ 值。但是,这种关系是否具有普适性还有待探讨。
3. 应变强化对弹性模量的影响
若试件为塑性材料,被加载至塑性阶段后再卸载,则当材料返回平衡状态时,弹性应变消失,而塑性应变不会消失,结果材料出现永久变形,如图a所示。该过程称为应变强化或者冷作硬化。这样,虽然比例极限提高了,但是在一定程度上降低了塑性,增加了脆性[1-2,4]。从图a中可以看出,强化前后,曲线线性段的直线趋于平行,斜率相同,弹性模量相同。实际上,试件从A’点卸载,再加载至同一点会损失部分热量或能量,因而加载和卸载过程的曲线并不重合,如图b虚线所示,会存在一个机械滞回区。在选择振动结构或机械设备的阻尼器材料时,要重点考虑其机械滞回特性[4]。
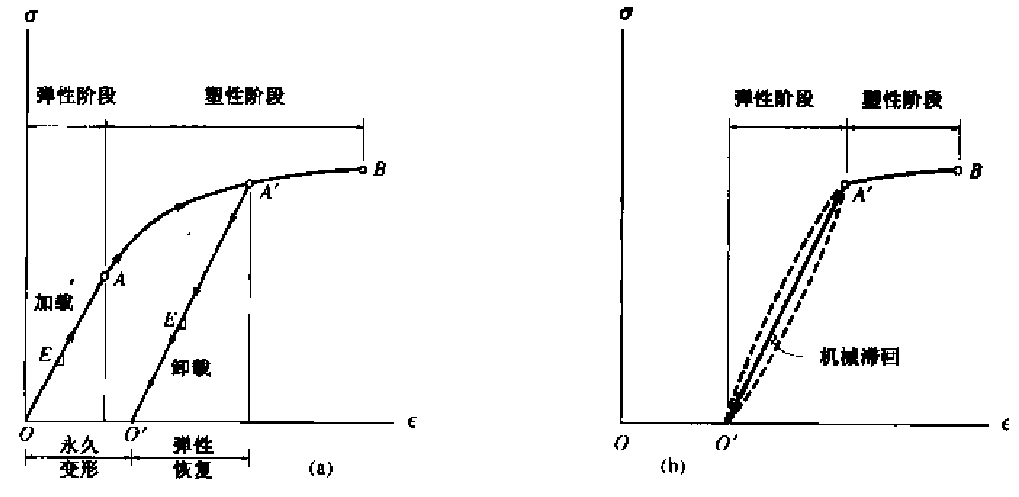
材料强化过程示意图 (源于文献[4])
4. 冷塑变形对弹性模量的影响
冷塑变形使弹性模量稍有降低,一般降低4%~6%,这与残余应力有关。当塑性变形量很大时,因产生形变使弹性模量出现各向异性,沿变形方向弹性模量最大[10]。文献[13]中指出,这种冷塑变形所造成的材料弹性模量变化,将会对精密零件的冷成型精度造成影响。
5. 温度对弹性模量的影响
温度升高,原子间间距增大,弹性模量降低。碳钢加热时,每升高100℃,弹性模量下降3%~5%,但在-50℃~50℃范围内,钢的弹性模量变化不大[10]。
6. 加载速率对弹性模量的影响
文献[9]中指出:由于弹性形变是以声速在介质内传播,金属介质中的声速相当大,如在钢中为4982m/s;而普通的摆锤冲击试验时,绝对变形速率只有4~5.5m/s,即使高速冲击试验的变形速率也在10³m/s以内,在这样的冲击载荷下,弹性形变总能紧跟上冲击外力的变化,因而应变率对金属材料的弹性行为及弹性模量没有影响。
现代机器中,各种不同件的应变率范围为10-6~106s-1。如静拉伸试验的应变率为10-5~10-2s-1(称为准静态应变速率),冲击载荷的应变速率为102~104s-1,称为高应变速率。此外,还有应变速率处于10-2~102s-1的中等应变速率试验,如落锤、旋转飞轮等。实践表明,应变速率在10-4~10-2s-1内,材料的力学性能没有明显的变化,可按静载荷处理。当应变载荷速率大于10-2s-1时,材料的力学性能将发生显著变化,这就必须考虑到应变率增大而带来的力学性能一系列变化。
在塑性变形阶段,随着加载速率的增加,变形的增长比较缓慢,因而当加载速率很快时,塑性变形来不及充分进行,这就表现为弹性极限,屈服强度等微量塑性变形抗力的提高。同时还发现,冲击载荷下塑性变形比较集中在某些局部区域,这反映了塑性变形是极不均匀的。这种不均匀的情况也限制了塑性变形的发展,使塑性变形不能充分进行,导致屈服强度、抗拉强度提高,且屈服强度提高得较多,抗拉强度提高得较少。
探讨:冲击载荷下塑性变形的不均匀性具体如何体现,与应力集中相关吗?
从以上文献对弹性模量影响因素和影响程度的介绍可以看出,当材料处于室温弹性阶段时,其弹性模量相对比较稳定,可以认为是常数;但对某些精密元件的设计,分析中仍需要考虑其变化对产品精度的影响;其次还需要看到,虽然材料的弹性模量比较稳定,但是切变模量却有可能有大的变化,由此来看材料的泊松比可能会是改变的。一般在线弹性分析范围内,弹性模量和泊松比是必须的参数,虽然弹性模量稳定,但若泊松比发生改变仍会影响计算精度。
审核编辑 :李倩
-
优化铜互连结构的热应力分析与介电材料选择2024-12-03 1460
-
影响应变计灵敏系数的因素有哪些?2024-10-25 1142
-
导热塑料弹性模量、脆性的影响及切削参数的合理选择2020-04-01 2165
-
哪里可以找到无线参数弹性模量的PSoC 5?2019-08-09 1156
-
磁流变弹性体压缩弹性模量测试分析2018-03-10 1344
-
双材料的载荷位移特征研究2018-03-05 832
-
基于DSP的木材弹性模量无损检测技术解析2017-10-31 1053
-
机器人常用材料2017-09-04 5380
-
TM J-A人造板弹性模量无损检测显示机的误差因素分析2009-07-09 595
-
用拉伸法测金属丝的杨氏弹性模量2009-06-09 2439
-
用拉伸法测定金属丝的杨氏弹性模量2008-12-03 4042
-
拉伸法测弹性模量.ppt2008-11-24 794
全部0条评论

快来发表一下你的评论吧 !

