

基于Matlab有限元编程的变截面悬臂梁分析
电子说
描述
导读:大家好,我是SimPC博士,主要从事工程结构抗震及减隔震研究,玻璃成型热工设备流动及传热研究,玻璃材料力学性能研究。精通有限元等数值算法的实现,有限元软件二次开发,数据处理,偏微分方程求解,优化算法,GUI界面开发等。有多项科研成果,其中SCI论文4篇,EI3篇,专利2篇。
近日我注册并认证了仿真秀专栏,将在仿真秀官网和App给平台用户带来Matlab有限元编程、复杂函数拟合和matlab绘图相关内容。此外还会带来隔震建筑Abaqus建模仿真分析等内容。本次案例主要以受均布荷载和集中荷载的变截面悬臂梁为研究对象,通过matlab编制四节点和八节点四边形单元有限元程序来对悬臂梁进行受力分析。
一、问题概述
如图1-1 所示,某变截面悬臂梁长度为2m,截面面积由0.6m至0.2m线性变化,受作用在自由端节点的集中荷载2P=kN和竖直方向均布荷载q=1kN/m作用,按平面应力问题分析,求解自由端节点挠度。变截面悬臂梁采用C30混凝土,弹性模量为E= 4 3 10 MPa,泊松比为。编制四节点和八节点四边形单元有限元程序,最终得到梁的变形。
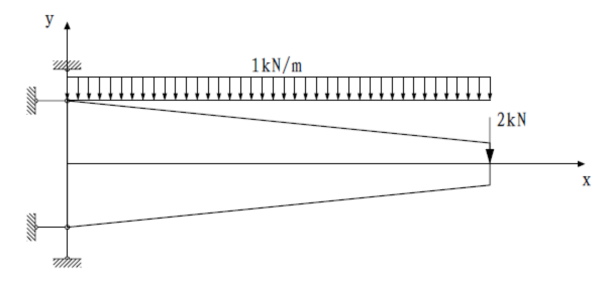
图1-1 变截面悬臂梁
二、求解思路
对于本问题采用基于MATLAB 编制有限元分析程序进行求解,其基本组成部分包括前处理模块、分析主程序模块和后处理模块。在前处理模块中,实现节点坐标输入、单元节点编号、网络划分以及边界条件输入等工作;在分析主程序模块中,求解整体刚度方程;在后处理模块中,实现结果显示、数据输出等工作。本文主要针对四节点四边形单元与八节点四边形单元理论和对应的计算程序进行讲解。
有限元法的基本步骤:
-
几何域离散,获得标准化的单元;
-
通过能量原理(虚功原理或最小势能原理,获得单元刚度方程;
-
单元的集成(装配);
-
处理位移边界条件;
-
计算支反力;
- 计算单元的其他物理量(应力应变)。
-
节点描述
-
场描述
- 单元刚度方程。
1、平面问题的平衡方程、几何方程、物理方程
平面问题的弹性力学基础理论是推导有限元方程的基础,所以先罗列出平面问题的平衡方程、几何方程、物理方程,具体如公式(1)-(3)所示。至于这些方程的推导过程大家可以参考任意弹性力学课本,都会进行详细的讲解。
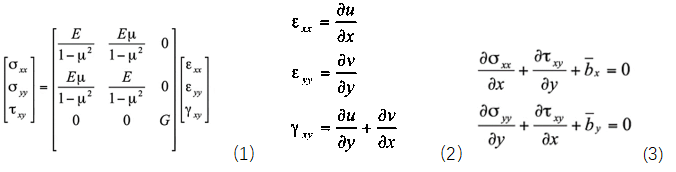
2、等参单元
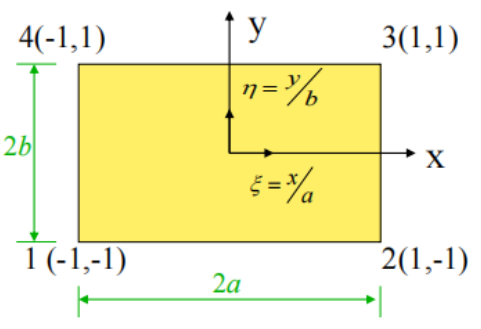
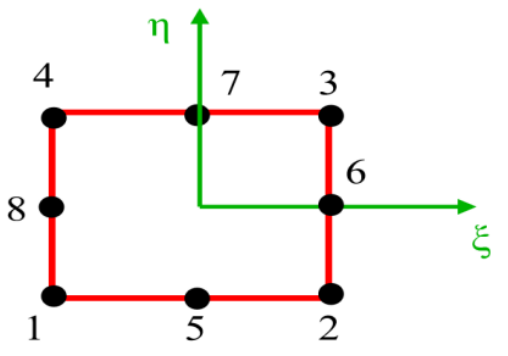
在有限元方法中,若要离散边界为曲线或曲面的求解域,需要建立将形状规则的单元变换为边界为曲线或曲面的单元的方法,在有限元法中对应此问题所采用的变换方法是等参变换,即单元几何形状的变换和单元内长函数采用相同数目的节点及相同的插值函数进行变换。同样我们今天要讲的四边形单元也从其对应的等参单元的基础理论讲起。四边形单元可以由自然坐标系中的矩形单元映射而成,映射关系如图2-1所示。
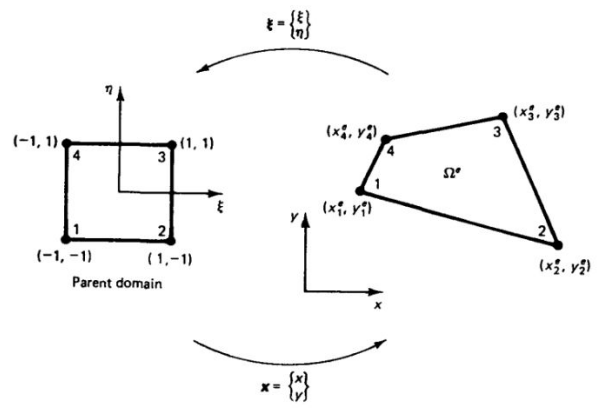
图2-1 平面四节点矩形单元的映射关系
在自然坐标系下,矩形单元是规则化的,当自然坐标系中的单元取为双线性单元时(也即为四节点四边形单元),平面四节点矩形单元如图2-2所示,单元有4个节点,8个自由度。单元的形函数定义如下: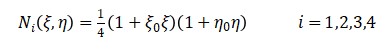
(4)其中,
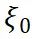 和
和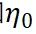 为自然坐标系下的节点坐标值。单元从自然坐标系到物理坐标系的映射为
为自然坐标系下的节点坐标值。单元从自然坐标系到物理坐标系的映射为

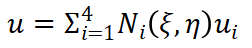 (7)
(7)
function N=ShapeFun(s,t)N1=1/4*(1-s)*(1-t);N2=1/4*(1+s)*(1-t);N3=1/4*(1+s)*(1+t);N4=1/4*(1-s)*(1+t);N=[N1 0 N2 0 N3 0 N4 0;0 N1 0 N2 0 N3 0 N4];end
同理平面八节点矩形单元如图2-3所示,单元共有8个节点,16个自由度。单元的形函数定义如下:
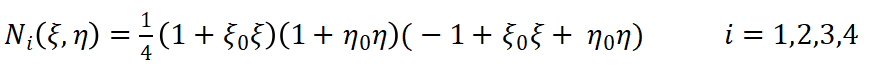 (8)
(8)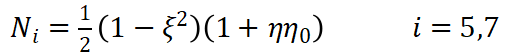 (9)
(9)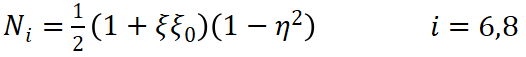 (10)
(10)其中,
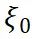 和
和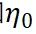 为自然坐标系下的节点坐标值。单元从自然坐标系到物理坐标系的映射为
为自然坐标系下的节点坐标值。单元从自然坐标系到物理坐标系的映射为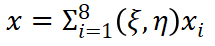 (11)
(11) 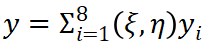 (12)
(12)在进行映射变换时候,要求单元两个坐标系下的节点编号要对应。单元的节点变量用型函数进行插值,有
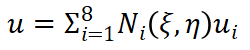 (13)
(13)
function N=ShapeFun(s,t)%% 四边形八结点等参单元形函数矩阵% 角点N1=1/4*(1-s)*(1+t)*(-s+t-1);N2=1/4*(1-s)*(1-t)*(-s-t-1);N3=1/4*(1+s)*(1-t)*(s-t-1);N4=1/4*(1+s)*(1+t)*(s+t-1);% 边中点N5=1/2*(1-t^2)*(1-s);N7=1/2*(1-t^2)*(1+s);N6=1/2*(1-s^2)*(1-t);N8=1/2*(1-s^2)*(1+t);N=[N1 0 N2 0 N3 0 N4 0 N5 0 N6 0 N7 0 N8 0;0 N1 0 N2 0 N3 0 N4 0 N5 0 N6 0 N7 0 N8];
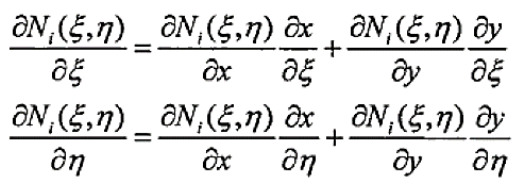 (14)
(14)写成矩阵的形式就是
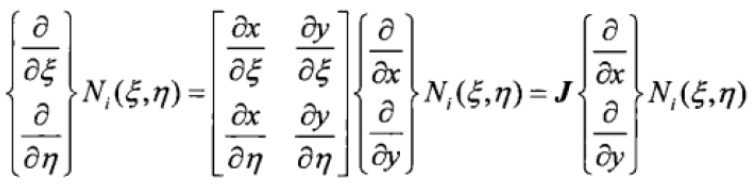 (15)
(15)其中,J被称为Jacobi矩阵。反过来,形函数对物理坐标的导数为
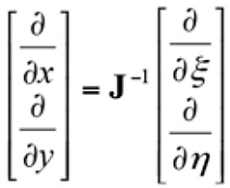 (16)
(16)另外,对于二维平面单元还要完成面积的映射,为
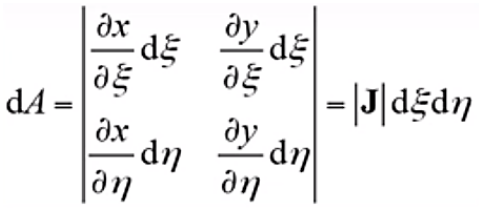 (17)
(17)可以看出Jacob矩阵在等参变化中扮演着至关重要的角色,Jacob矩阵具体的表达式如下所示,
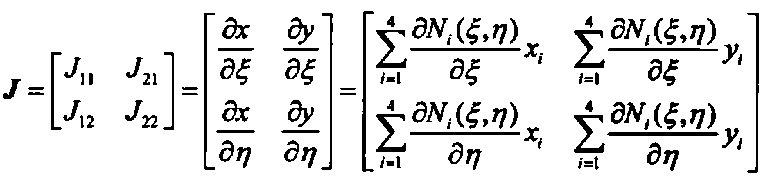 (18)
(18)公式18对应的八节点单元雅各比矩阵的求解代码为:
公式18对应的四节点单元雅各比矩阵的求解代码为:function J=Jacobi(ie,s,t,Elements,Nodes)ENodes = Elements(ie,:); %获取单元结点xe = Nodes(ENodes(:),:); %获取节点坐标x1=xe(1,1);y1=xe(1,2);x2=xe(2,1);y2=xe(2,2);x3=xe(3,1);y3=xe(3,2);x4=xe(4,1);y4=xe(4,2);J=1/4*[-(1+t) -(1-t) 1-t 1+t;1-s -(1-s) -(1+s) 1+s]*[x1 y1;x2 y2;x3 y3;x4 y4];end
3、刚度矩阵的推导function J=Jacobi(ie,kesi,yita,Elements,Nodes)ENodes = Elements(ie,:); %获取单元结点xe = Nodes(ENodes(:),:); %获取结点坐标x1=xe(1,1);y1=xe(1,2);x2=xe(2,1);y2=xe(2,2);x3=xe(3,1);y3=xe(3,2);x4=xe(4,1);y4=xe(4,2);J=1/4*[-(1-yita),(1-yita),(1+yita),-(1+yita);-(1-kesi),-(1+kesi),(1+kesi),(1-kesi)]*[x1 y1;x2 y2;x3 y3;x4 y4];end
为了求出上述平面四节点和八节点单元的单元刚度矩阵,需要借助能量原理(虚功原理、最小势能原理)进行推导,能量原理的推导过程大家可以参考任意一本有限元理论书籍,都会有详细的推导过程,这里就不做进一步推导讲解,直接给出物理坐标和几何坐标系下的刚度矩阵的公式
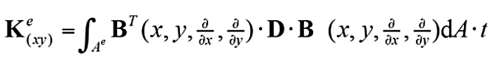 (19)
(19)
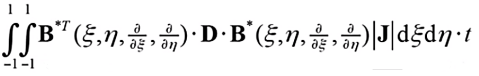 (20)
(20)
其中B矩阵为应变矩阵,如下式;D矩阵为材料刚度矩阵,如公式(1)所示,是物理方程中表征应力应变关系的矩阵。从上述刚度矩阵的表达式可以看出,自然坐标和物理坐标间要完成坐标映射、偏导映射、面积隐射三个部分,具体映射公式已在上一节的等参单元讲解中详细给出。
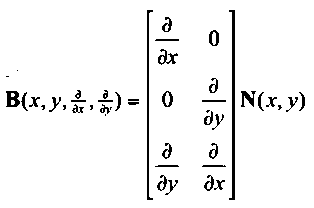 (21)
(21)
4、高斯积分
公式(20)中的单元刚度矩阵通过数值积分求得,本案例中的四节点和八节点四边形等参单元均采用2*2个积分点的高斯积分即可求得精确结果。高斯积分点的坐标具体如图所示。
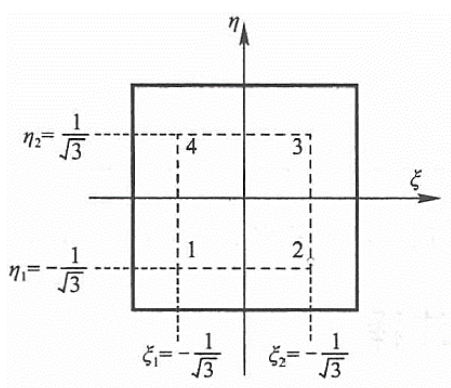
4-1 Gauss积分点示意图
公式(20)写成数值积分的形式为
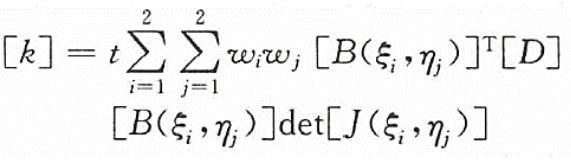 (22)
(22)
对于8节点单元实现上述数值积分的代码如下所示:
r = [-sqrt(1/3) sqrt(1/3)]; % 2*2 高斯积分点s = [r(1) r(1) r(2) r(2)];t = [r(2) r(1) r(1) r(2)]; % 高斯积分点坐标for i=1:4J = Jacobi(E_ID,s(i),t(i),Elements,Nodes); % 雅可比矩阵Nst = DiffShapeFun(s(i),t(i)); % 形函数关于自然坐标s,t求导Nxy = zeros(8,2);for j=1:8:) = (JNst(j,:)')'; % 形函数关于 x,y 求导=inv(J)*NstendBm = [Nxy(1,1) 0 Nxy(2,1) 0 Nxy(3,1) 0 Nxy(4,1) 0 Nxy(5,1) 0 Nxy(6,1) 0 Nxy(7,1) 0 Nxy(8,1) 0;0 Nxy(1,2) 0 Nxy(2,2) 0 Nxy(3,2) 0 Nxy(4,2) 0 Nxy(5,2) 0 Nxy(6,2) 0 Nxy(7,2) 0 Nxy(8,2);Nxy(1,1) Nxy(2,2) Nxy(2,1) Nxy(3,2) Nxy(3,1) Nxy(4,2) Nxy(4,1) Nxy(5,2) Nxy(5,1) Nxy(6,2) Nxy(6,1) Nxy(7,2) Nxy(7,1) Nxy(8,2) Nxy(8,1)];ke = ke+det(J)*Bm'*D*Bm*Width; %数值积分end
5、均布荷载的施加
在有限元中分布力要转为等效节点荷载,而确定等效节点荷载的方法也是通过能量原理推导得到
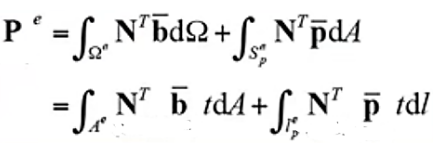 (22)
(22)
上式中,第一项代表体积力的等效荷载,第二项代表面积力的等效荷载,这个案例我们只考虑面力荷载。实现公式22的代码为
function Pe=UniLoad(ie,N_ID_p1,q0,Nodes,Elements)k=-0.625e-3; % 均布荷载值 N/mms = [-sqrt(1/3) sqrt(1/3)]; % 2*2 高斯积分点ENodes = N_ID_p1(ie,:); %获取单元结点号Pe=zeros(16,1); %生成临时单元节点力零列向量x1=Nodes(ENodes(1),1);x6=Nodes(ENodes(4),1);L16=abs(x6-x1); %单元长度for i=1:2 %用于高斯积分的求和循环N_q=ShapeFun(s(i),1); % 4级子程序:ShapeFun(s(i),1)q_x=q0;Pe=Pe+N_q'*q_x*[0;L16/2];endend
三、Matlab有限元编程精品课
网格划分及变形结果如图3-1所示。本案例的详细视频教程和对应的matlab源码,请关注我的仿真秀官网和APP精品课程《Matlab有限元编程从入门到精通10讲》。

图3-1 梁变形结果
-
 青衣na
2023-11-26
0 回复 举报求完整的代码 收起回复
青衣na
2023-11-26
0 回复 举报求完整的代码 收起回复
-
电压放大器在自感知的悬臂梁变形控制研究中的应用2025-03-06 665
-
基于六面体单元热应力问题的Matlab有限元编程求解2022-11-17 4122
-
基于箱形梁CADCAE有限元分析2021-07-26 840
-
悬臂梁称重传感器的工作原理2021-05-11 12315
-
华盛顿大学利用悬臂梁开发出激光制冷新技术2020-07-01 3027
-
悬臂梁式传感器的原理是什么?2019-11-04 5195
-
测量仪悬臂梁拓扑优化2018-03-27 1312
-
一种基于MEMS的新型镂空压电悬臂梁能量采集器2017-01-07 872
-
采用环梁加固风机基础的有限元分析2017-01-02 873
-
基于comsol的悬臂梁形变实验报告2016-04-15 1656
-
【PDF】matlab有限元法计算分析程序编写2011-02-28 7115
-
静电式微开关硅悬臂梁的变形分析2010-01-01 683
-
利用微电铸制作镍悬臂梁2009-12-29 643
-
双孔悬臂梁应变传感器—称重实验2009-03-06 10678
全部0条评论

快来发表一下你的评论吧 !

