如何在实际电路中使用带通滤波器

每个模拟设计师的噩梦都是处理电路中的噪声。当涉及到开关电路或音频放大器或频率信号电路时，电路很可能会受到噪声信号的影响。在从电路中去除噪声的许多方法中，最常用的一种称为滤波器电路。顾名思义，该电路将从实际信号中滤除不需要的信号（噪声）。滤波器电路有很多种，但最常用和最有效的一种是带通滤波器，它可以使用一对电阻器和电容器轻松构建。因此，在本教程中，我们将了解此带通滤波器、其背后的理论以及如何在实际电路中使用它。

什么是带通滤波器？

带通滤波器电路/设备用于仅允许一组预定义的频率通过它。它将过滤掉所有低于设定值和高于设定值的频率。它是高通滤波器和低通滤波器的组合。只允许高于它的频率的滤波器称为高通滤波器，只允许低于它的频率的滤波器称为低通滤波器。可以通过级联高通和低通滤波器来获得带通滤波器。它在音频放大器电路和无线收发器中有着巨大的应用，扬声器必须只播放所需的一组频率而忽略其余部分。

有两种类型的带通滤波器。如果电路涉及某种外部电源（有源器件），如晶体管等，则该电路称为有源带通滤波器，如果电路不涉及任何有源元件且仅由电阻器、电容器和电感器等无源元件组成，则该电路称为无源带通滤波器。在本文中，我们将详细讨论无源带通滤波器。除此分类外，本文将简要介绍过滤器可以分类的其他方面。

带通滤波器电路

如前所述，我们将讨论使用电阻器和电容器构造的无源带通滤波器。它是高通滤波器和低通滤波器的组合。一个简单的无源带通滤波器的示例电路图如下所示。

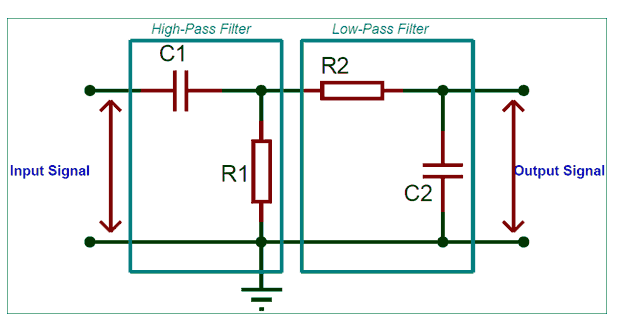
电路的前半部分是一个高通滤波器，它过滤低频并只允许高于设置的高截止频率（fc HIGH）的频率。这个高截止频率的值可以使用公式计算

fc高= 1 / 2 π*R1*C1

电路的后半部分是低通滤波器电路，它过滤较高的频率，只允许低于设定的低截止频率（fc LOW）的频率。可以使用公式计算低截止频率的值

fc低= 1 / 2 π*R2*C2

这种类型的滤波器电路被称为二阶滤波器，因为它有两个电阻器和两个电容器。带通滤波器可以是二阶滤波器或更高阶滤波器，因为电路的正常运行至少需要两个电阻器和电容器。现在，当向该滤波器提供输入信号频率时，它会输出高于 fc LOW 且低于 fc HIGH 的频率。换句话说，输出频率可以由fc HIGH- fc LOW给出，位于该区域之间的频率称为带宽。因此，滤波器的带宽可以计算为

带宽 = fc HIGH- fc LOW

带通滤波器的频率响应

2阶无源带通滤波器的频率响应又名波特图曲线如下所示。

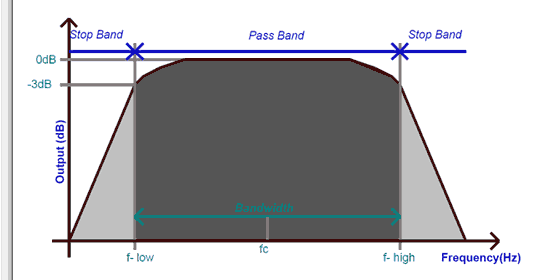
该图是针对 X 轴的输入频率和 Y 轴的输出分贝绘制的。当输入频率小于较低的截止频率（f-low）时，输出保持小于-3dB，当超过该频率时，输出达到最大值并保持在那里，直到频率超过较高的截止频率（f-高）。输出增益保持最大的峰值称为谐振频率。它只是上限较高截止频率和较低截止频率的几何平均值。计算公式如下

谐振频率 （Fr） = √（f - 低 * f - 高）

较低截止频率和较高截止频率之间的距离称为带宽。因此，只有在带宽限制范围内，才允许输入频率通过。

带通滤波器的实际例子

让我们构建一个简单的带通滤波器来滤除一组频率并检查它的实际工作原理。我在本教程中使用的实验设置如下所示

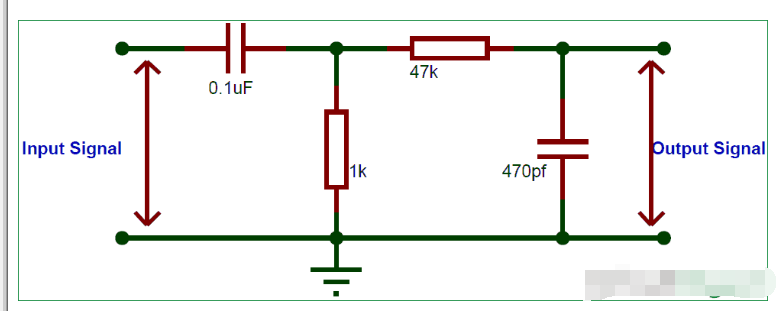
如您所见，高通滤波器是使用电容器 0.1uF （C1） 和电阻器 1K （R1） 构成的。因此，该电路的较高截止频率将是

fc高= 1 / 2π*R1*C1

= 1/（2*3.17*1*10^3*0.1*10^-6）

=1577 赫兹

低通滤波器由电容器 470pF （C2） 和电阻器 87K （R2） 构成。该电路的下限截止频率可以计算如下

fc低= 1 / 2π*R2*C2

= 1/（2*3.14*8.7*10^3*470*10^-12）

=7280赫兹

从上面的计算我们可以推断出电路将只允许 1577 Hz 到 7280 HZ 范围内的频率，任何小于或大于此的频率都将被我们的带通滤波器滤除。让我们通过在面包板上构建电路来检查是否相同。我的测试设置如下所示

为了测试电路，我们需要一个函数发生器来产生频率可以控制的信号频率。因为我没有，所以我决定使用我的手机，它有一个安卓应用程序，可以通过我的 3.5 毫米耳机插孔生成所需的频率。然后使用如上所示的插孔将该信号作为输入频率提供给电路。

为了检查我使用示波器测量输入信号频率的应用程序的依赖性，发现生成频率很容易。下图显示了我手机上的应用程序，它产生大约 4，819 Hz 的输入频率，连接到它的示波器显示信号并测量 4.816 KHz 的频率，这是完美的。

现在，我们可以将示波器连接到电路的输出信号并改变输入频率。该电路将允许在 1500 到 7000 之间的所有频率显示在示波器上，而其他频率将被过滤掉或产生噪音。另请记住，该电路仅用于理解目的，因此在实际应用之前需要进行改进。此外，由于电路是在面包板上构建的，因此输出信号可能会吸收一些噪声，请将电容器尽可能靠近并减少其引线的长度以减少问题。