

“万能”的PID
描述
最近跟一个同事聊了聊天,他说一直用的位置式PID,从来没在具体项目中用过增量式PID,感觉两者没啥区别呀?
于是跟他讨论了一番,不由得让人深思~
1
“万能”的PID
PID是一种非常经典的控制类算法,凭着它的简单易用在工程上得到了广泛的应用,并且影响力也是极高,那为什么说其简单易用呢?
可以说只要你对PID的主要的参数对系统的影响理解得足够好,完全可以通过手动试凑的方式来获得一套合适的PID参考,所以对一些非控制类的工程师应用起来也是非常友好的。
当然还有一个非常重要的原因,PID算法对大部分系统稳定性、鲁棒性以及可靠性都非常的高,有调试PID控制算法经验的朋友应该都有类似的感觉,即便根据经验随便给系统一套参数都可以到达一个不错的控制效果。
所以在很多人眼里这算法就是"万能的",适应的场景也非常的广泛,然而自古有一种规律"熊掌和鱼不可以兼得",PID算法虽然适应性非常广泛,对于处理一些特定的应用场景,或许其并不会最优的解决办法。
基于大家在实际应用中各种各样的需求,曾经一个发展涌现了非常的PID的变种,也就是对PID算法在特定的应用场景进行优化、或者与其他一些控制方法进行结合,以便达到相应控制场景下的不错控制效果,比如微分先行PID、PID与智能控制的算法的结合等等。
当然如果PID算法实在无法满足需求了,那也不能勉强,就只能考虑寻找另外更为匹配的控制策略,比如现在非常流行的自抗扰控制技术等等。
2
PID的理解
PID算法主要就是三项,比例(P)-积分(I)-微分(D),在连续的时间域内的表达式如下:
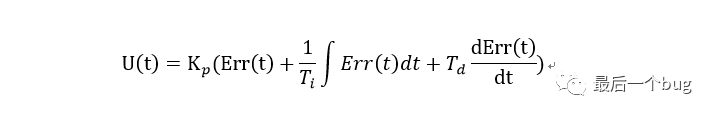
从上面的公式可以看出PID算法是一个非常纯粹的数学表达式,既然是数学表达式那必然可以通过数学的方式进行分析,拉式变换一下,获得传递函数,然后采用控制理论分析方法,结合被控对象分析其对动态系统的稳定性、准确性以及快速性进行分析,从而达到性能上的最优解,这个控制系统的设计过程不是本文重点,暂时就不进行展开了。
还记得最开始了解这个算法的时候,有一句话非常相信的彰显其魅力所在:P-I-D分别代表着当前、过去和未来。P对当前误差的抑制作用;I对历史误差的累积控制,以便消除静态误差;D根据误差的变化率进行补偿,从表达式也非常容易从根本上理解这几句话。
3
数字PID
在前面跟大家简单描述了连续域内的PID算法表达式,而连续域中该算法需要通过相应的模拟电路来进行实现,特别是一些没有数字芯片的嵌入式系统是经常可见的。
但随着数字系统的应用,特别是单片机系统,数字PID更加得到广泛的应用,被大部分人所熟知的两种数字PID,分别是位置式PID和增量式PID。
大部分的教材都会描述着两种形式的数字PID,然而这些教材一上来就介绍位置式PID与历史状态相关,过去会对现在的控制输出产生影响,而增量式PID仅仅只与最近的几次误差数据相关。
如下是位置式PID表达式:
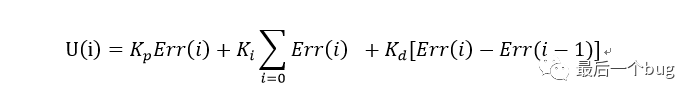
而增量式PID的形式则可以通过位置式进行如下表达式处理得到:
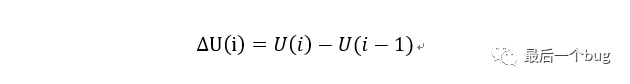
如下便可以得到增量式的表达式:
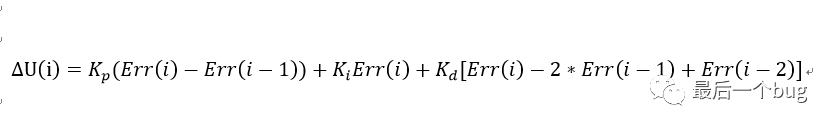
这样看来增量式PID只与最近的两次误差有关系,不会存在累积误差的问题,说来增量式PID必然是更好的,那为何还要介绍位置式PID呢?
也有伙计在自己的程序中使用增量式PID的表达式,毕竟增量式PID其输出仅仅只是控制量的增量,最后还是需要把输出量进行累积,这与位置式根本没啥区别。
于是很多初学者,甚至一些用PID多年的工程师对此都抱有一丝疑问。
其实这两种数字PID的应用场景是有区别的,增量式PID控制输出的仅仅只是控制量的增量,其主要是应用在执行机构带有积分部件的被控对象,而位置式PID其输出的是实际的控制量,则用于不带积分环节的执行机构。
当然如果在一些不带积分环节的执行结构系统中你执意要使用增量PID的形式也无伤大雅,只是最后用数字积分进行处理后输出,其与位置式PID式没有差异,增量式PID的优势并没有展现,因为真正单独使用增量式PID的执行机构的积分环节是连续的,这是数字离散的方式无法比拟的。
审核编辑 :李倩
-
什么是单臂万能试验机?2023-03-03 1332
-
总结STM32控制中常见的PID算法 理解万能的PID算法2022-07-05 8257
-
一文总结万能的PID算法2022-06-17 4823
-
万能驱动下载链接.txt2021-12-30 1908
-
万能转换开关原理_万能转换开关结构2019-12-09 11375
-
万能角度尺怎么使用?2019-11-06 2448
-
万能电池怎么使用?2019-10-21 2135
-
万能协议通信工具2017-11-18 1272
-
电子万能试验机与液压万能试验机的区别2013-07-04 3358
-
自作万能充电宝2012-11-03 6705
-
万能遥控器设置方法_万能遥控器代码2012-09-14 191740
-
万能板的连线问题2011-10-27 2594
-
winxp万能声卡驱动,程序下载2009-04-21 2900
-
中星微万能驱动下载2008-01-11 898
全部0条评论

快来发表一下你的评论吧 !

