Bi2Se3和Bi2Te3系统中拓扑表面态的电子有利于氢还原过程

01 引言

电子晶体中存在“剩余”的电子，这些电子被束缚在晶格间隙的位置。这一特殊的电子结构有利于实现形成拓扑材料所需的能带翻转。并且在电子晶体中已经开发出具有拓扑性质的材料。电子晶体的拓扑状态提升了他们的实际应用价值，例如在催化领域。研究人员们发现费米弧或是表面状态可以促进分子吸附，在2011年陈等人报道了拓扑绝缘体Bi2Se3中的Dirac锥表面态可以调节CO的吸附能。随后，Catherine的团队证实了Bi2Se3和Bi2Te3系统中拓扑表面态的电子有利于氢还原过程。其次，Felser等人将拓扑绝缘体催化的概念扩展到Weyl半金属，如TaAs家族。然后，陈等人报道称节线半金属TiSi族的鼓膜表面态可以产生比Weyl半金属更高的表面活性。我们基于第一性原理计算，发现二维电子晶体［Ca2N］+·e-在低能区存在type-II Weyl点，导致其在边界处出现费米弧，并对其催化性能起重要作用。

02 成果简介

本课题组基于第一性原理计算方法和鸿之微DS-PAW软件等，从拓扑角度解释了氢在电子晶体［Ca2N］+·e-中的吸附机理。我们从能带结构来看在K-Γ路径上存在一个type-II Weyl点，这两条能带主要是由多余电子提供的，对氢的吸附过程有很大影响，特别是我们还发现type-II Weyl费米子与吸附能呈正相关。我们分别从层数、掺杂空穴浓度和应变三个方面验证了这一结论。具体而言，当type-II Weyl点更接近费米能级时，费米弧通过费米能级的能量窗口更大，导致边缘的态密度更高，进一步增强了氢吸附性能。

03 图文导读

图1显示单层和多层Ca2N的晶体结构以及布里渊区，单层Ca2N的晶格常数为a=b=3.56 Å，属于Rm空间群（编号166）。Ca2N由多个长程有序三层结构叠加而成，如图1（c）所示。值得注意的是，Ca2N中Ca和N的原子价分别为+2和-3，这意味着Ca2N的总价大于零，即遵循［Ca2N］+·e-的形式。然后，我们计算［Ca2N］+·e-的电子局域化函数（ELF），如图1（d）所示。结果表明，多余电子局域在中间层中，形成典型的二维电子气（2DEG），这与我们的价态分析结果非常吻合。

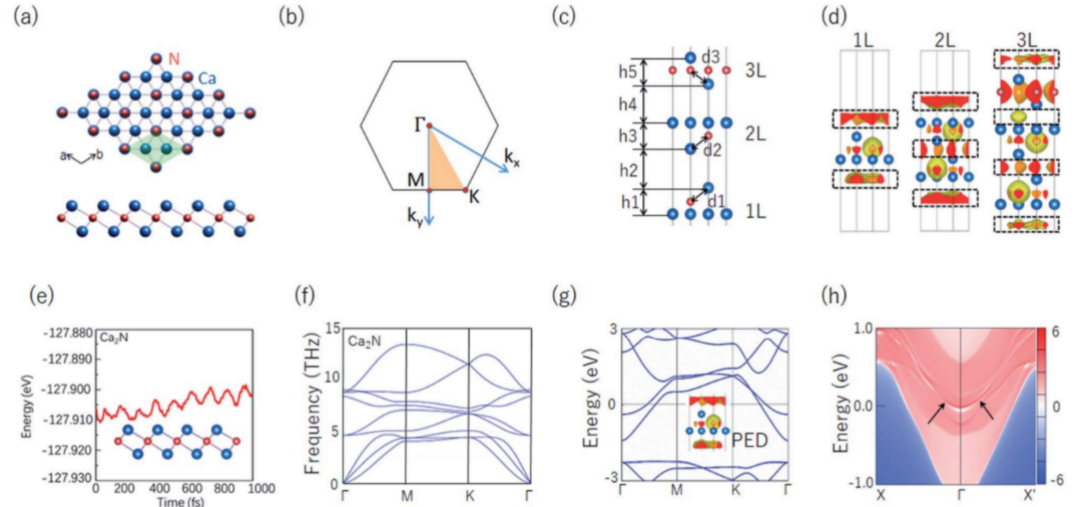
图1.（a）单层Ca2N的晶体结构。（b）单层Ca2N的布里渊区。（c）多层Ca2N的晶体结构，其中h1–5为层间间距，d1–3为Ca–N的长度。具体参数见表1。（b） 1层、2层和3层Ca2N的电子局域化函数（ELF），等表面积值设定为0.65。（e）和（f）单层Ca2N的动力学和热力学稳定性。（g）无SOC单层Ca2N的电子能带结构；插图显示了0.4–0.6 eV能量区的部分电子密度（PED）。等值面值选择为0.005玻尔。（h）单层Ca2N的边缘态。

表1.多层Ca2N的晶格常数（a=b）、层间距（h）和Ca–N（d）长度。

图2中我们考虑了Ca2N中三个不同的吸附位点，发现氢吸附在4×4×1的超胞结构下开始趋于稳定，对于最佳吸附位点F2、S2、T2，我们发现，随着层数的增加，其吸附能力逐渐减小，原因在于其type-ⅡWeyl点与费米能级的距离相关，从能带结构中我们发现，第二层的Weyl点仍然存在，而在第三层中消失了，但是其Weyl点距离费米能级的距离与氢的吸附能呈正相关，远小于单层的氢吸附能，因此Weyl点在电子晶体［Ca2N］+·e-的氢吸附中起着重要作用。

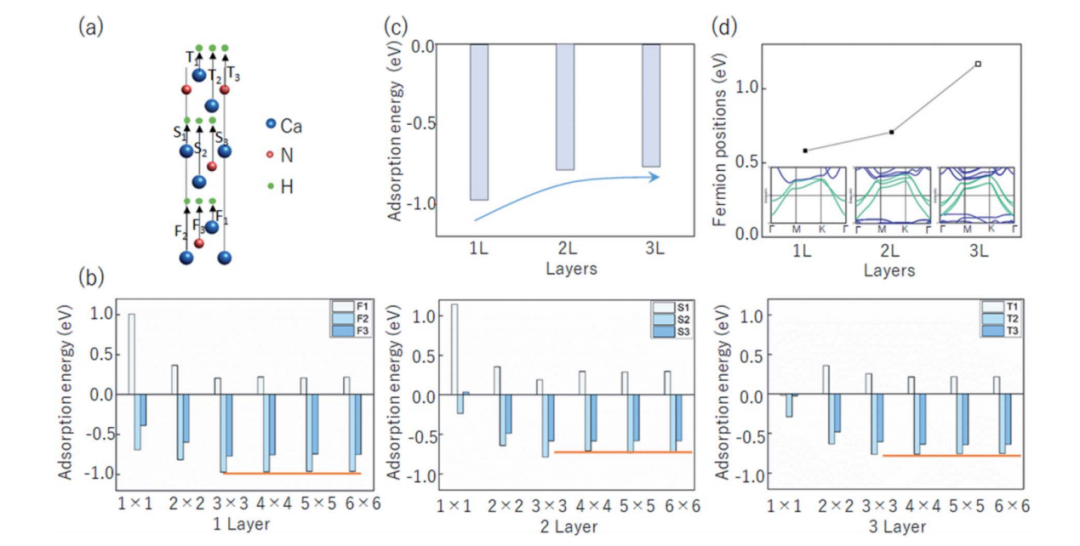
图2 （a） Ca2N在不同层的吸附位置。（b）不同层数下扩胞的吸附能。（c）最稳定的位点不同层下的吸附能。（d）1L、2L和3L下type-ⅡWeyl点与费米能级的距离及能带结构。

图3所示我们通过引入空穴来调节Ca2N电子晶体中多于电子的能带结构。当加入空穴增加到0.4eV时到达临界点，我们发现Weyl点在临界点时与费米能级的距离最近，相应的吸附能最大。当空穴的掺杂大于或是小于0.4eV时，Weyl点就会远离费米能级，此外当多余的电子被完全中和时，［Ca2N］+·e-便成为了半导体，此时的Ca2N不具备吸附能力，因此［Ca2N］+·e-的氢吸附能与Weyl点距离费米能级高度呈正相关。

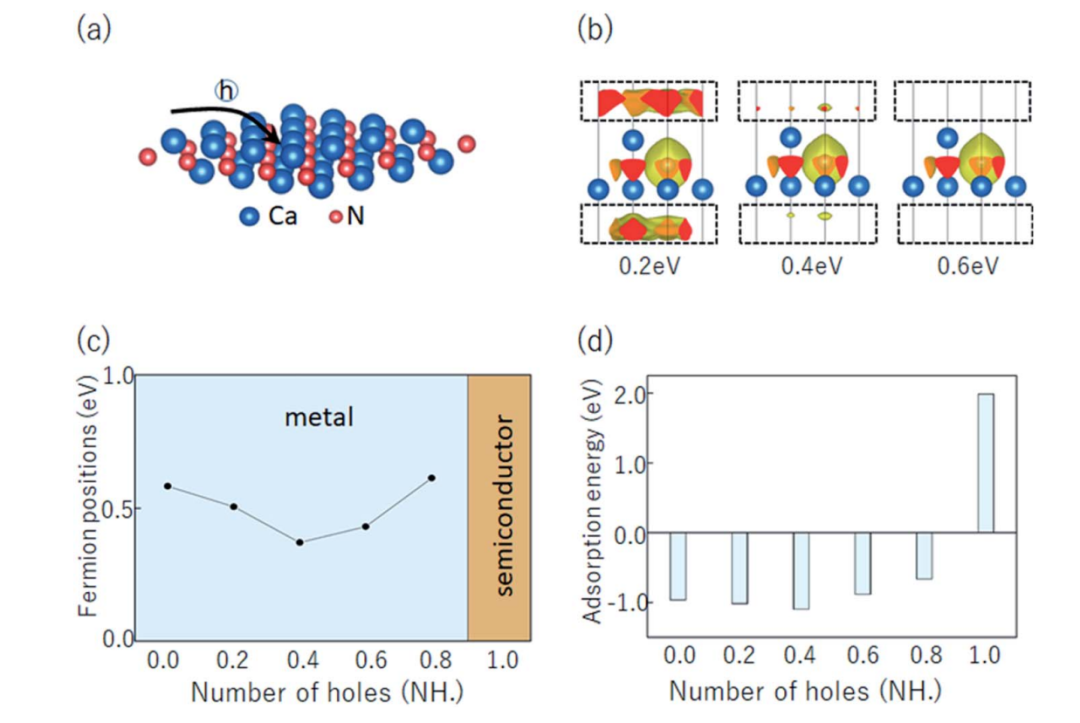
图3（a）空穴掺杂对电子结构调节示意图。（b）空穴掺杂的电子局域函数图，等值面为0.65。（c）掺杂空穴为0-1eV时Weyl点与费米能级的距离。（d）空穴掺杂时的氢吸附能。

图4我们通过施加应变而不掺杂空穴来调整Weyl点的位置。此时不破坏Ca2N的对称性，从而保留了Weyl点和电子晶体的特征，但是改变了Wyel点与费米能级的位置。我们发现从应变-6%到+6%，Weyl点距离费米能级越来越近，相应的氢吸附能力也逐渐增大。如果施加单轴应变则Weyl点就会打开间隙，氢吸附能力就会变小。

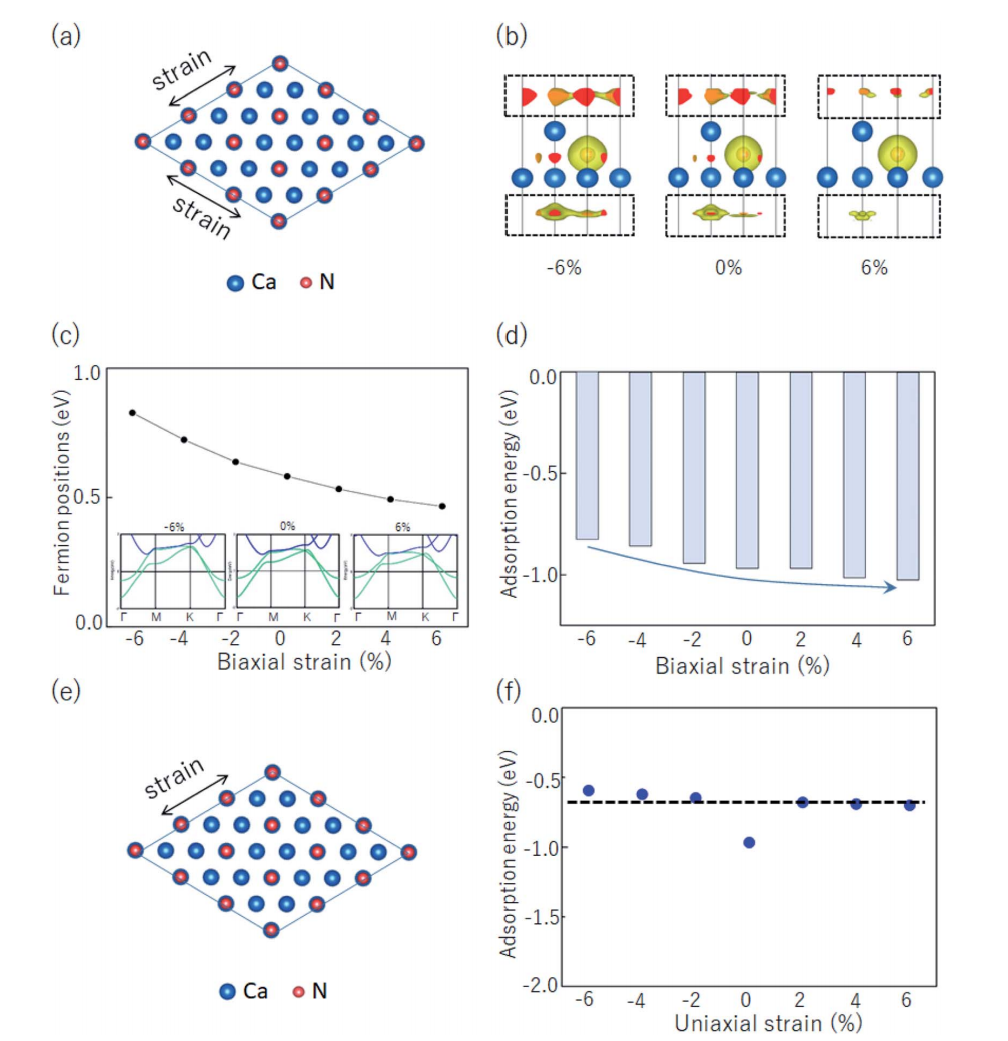
图4（a）施加等轴应变调节的电子结构图。（b）应变分别为-6%、0%和6%的电子局域函数，等表面值为0.65。（c）-6%~6%双轴应变下的Weyl点与费米能级的距离。（d） -6%~6%双轴应变的氢吸附能。（e）单轴应变调节的电子结构图。（f）单轴应变的氢吸附能。

图5是我们同时考虑掺杂和应变的协同作用，与上述结果一致，我们还推导了Weyl点距离费米能级和Ca2N中氢吸附效应之间的线性关系。具体而言，我们调节在不同应变下添加不同空穴数量以改变电子结构和氢吸附能的变化。结果表明，Weyl点距离费米能越来越近，随后离开费米能级，因此吸附能力先增大后减小。

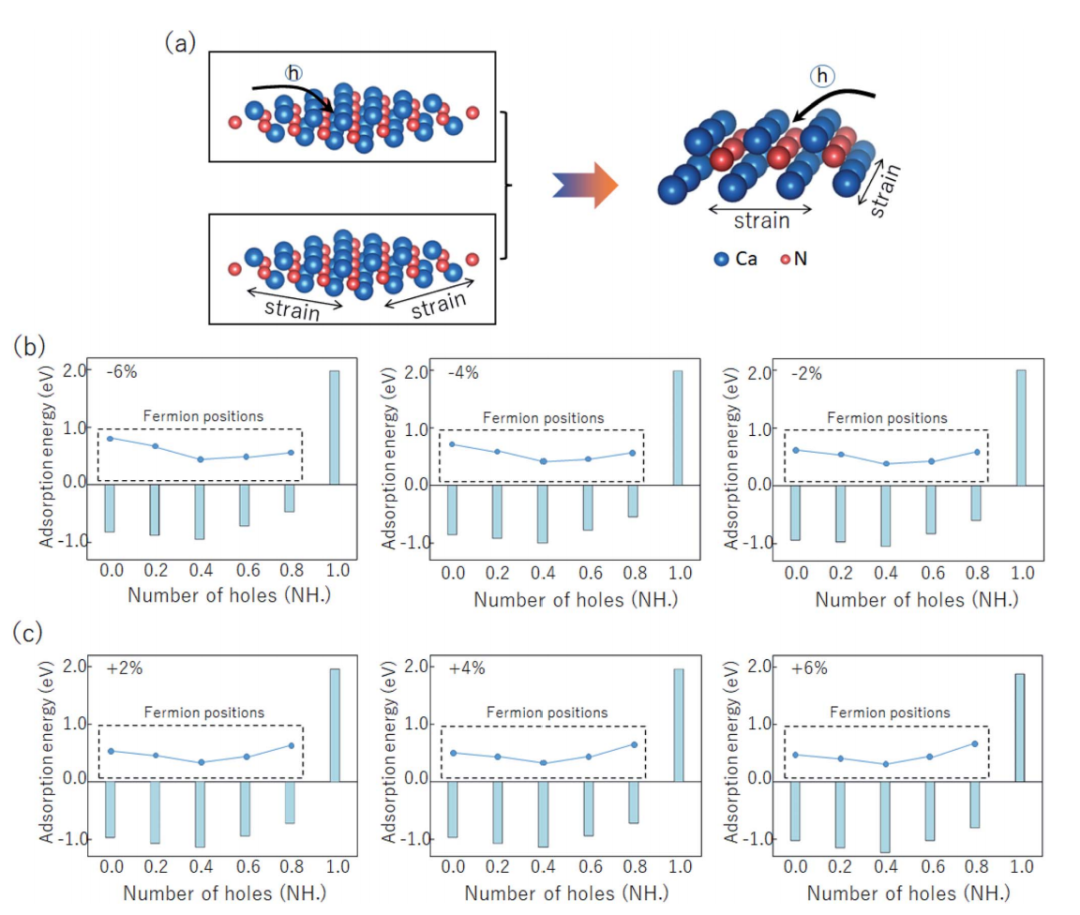
图5.（a）双轴应变和空穴掺杂的正交示意图。（b）和（c）不同空穴掺杂（0-1eV）在应变（-6%~6%）下的氢吸附能。插图为Weyl点与费米能级的距离。

图6所示，众所周知，本质上影响材料吸附能的是表面态密度，因此，费米弧的能量窗口是否穿过费米能级对表面态密度有重要的影响。图中显示了不同应变下的边缘态，结构表明，拉应变下费米弧的能量窗口均穿过费米能级，相应的其对应的边缘态的表面态密度就会更高，相反，压缩应变下费米弧不会穿过费米能级，因此边缘态对应的表面态密度就会比较低。

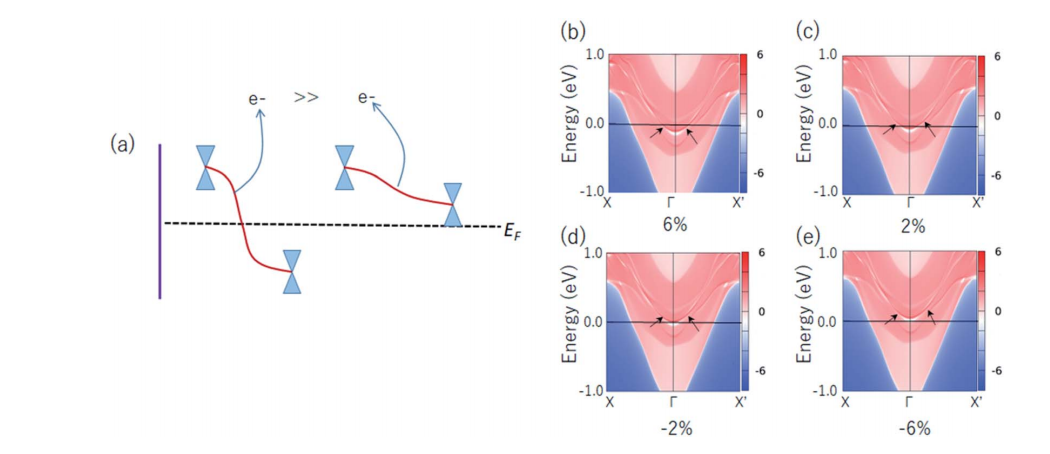
图6.（a）氢吸附过程中费米弧能量窗口给予电子能力示意图。其中费米弧能量窗口穿过费米能级的给电子能力远大于不通过费米能级的给电子能力。（b）单层Ca2N在-6%、-2%、2%和6%应变状态下的边缘态。

04 小结

我们基于第一性原理计算，发现二维电子晶体［Ca2N］+·e-在低能区存在type-II Weyl点，导致其在边界处出现费米弧，并对其催化性能起重要作用。因此我们通过对其层数、电子/空穴浓度和应变等方面来研究其吸附能量的变化，我们发现type-II Weyl费米子的位置与吸附能呈正相关。type-II Weyl点与吸附能之间的这种密切关系有助于电子晶体［Ca2N］+·e-的应用，为研究电子晶体中的氢吸附提供了新的思路。　　

      审核编辑：彭静