小波变换开关电流电路CAD设计

　　 用开关电流技术实现小波变换， 关键是小波滤波器的实现; 小波滤波器传输表达式可通过对小波基函数的有理逼近来获得。基于Pad 逼近的方法， 采用高斯函数族作为小波基函数， 对所选的高斯函数进行频域的有理分式逼近来获取小波滤波器传输表达式， 从数学上提出一种设计小波变换开关电流( SI)滤波器的CAD方法。结合SI的电流模信号特点， 利用双二次滤波器的性质， 用SI单元电路的级联结构来实现电路的灵活设计。设计举例给出了设计思路， MATLAB仿真结果显示这种方法的可行性。

　　1 系统框图及设计基本原理

　　提出设计小波变换S I滤波器的CAD 方法， 具体见框图1。先由用户选择小波基， 即确定高斯函数的参数， 以及采用其第N 阶导数作为小波基。然后， 选择Pad 逼近的方式， 得到时域或频域的有理分式之后， 可以利用SI滤波器的性质来用对应的SI单元电路的级联结构实现， 从而运用了SI技术的优点和性能优势。

　　使用Mat lab编程可以实现该CAD 系统， 它是一个窗口界面交互编程模式， 通过输入数据及点击菜单栏选择相应的菜单， 从而完成系统框图设计。采用M atlab可以实现Pad 逼近的小波基函数有理式逼近的算法， 通过从菜单输入高斯函数导数的阶数和尺度因子可以实现有理式表达式的CAD; 而SI电路具有模块化设计的特点同时开关电流滤波器的时间常数由晶体管的宽长比或时钟的频率决定， 实现基本小波滤波器后只需要调节时钟频率即可实现不同尺度的其他滤波器。

　　

 

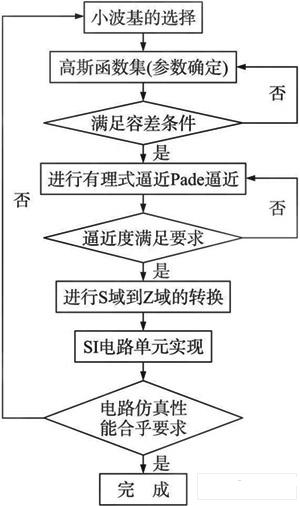
　　图1 系统框图

　　1. 1 开关电流技术

　　S I电路由受时钟控制的开关、电流镜等电路构成， 利用MOS器件栅- 源间电容存储效应实现对电流信号的处理。在实现线性离散电路系统设计时需要的基本单元有三个: 加法器， 乘法器和贮存单元;当用SI电路实现时， 其分别对应SI电路的基本单元为结点——电流信号的相加、比例电流镜和S&H(取样保持)单元， 这样使电路的设计可以模块化而大大简化电路的设计。利用SI基本单元可以组成积分器而实现不同品质因数的滤波器， 最终达到小波变换电路设计的目的。

　　另外， 用信号流程图的观点来理解S I基本电路， 可以使系统传输函数的SI实现更明了。如通用积分器的SI电路设计， 可由同向输入， 反向输入和放大输入叠加构成， 如图2所示。

　　输出电流为:

　　

 

　　当i1 ( z ) = - i2 ( z ) = i( z ) /2， a1 = a2 = a 构成双线性积分器， Z 域传输函数为:

　　

 

　　

 

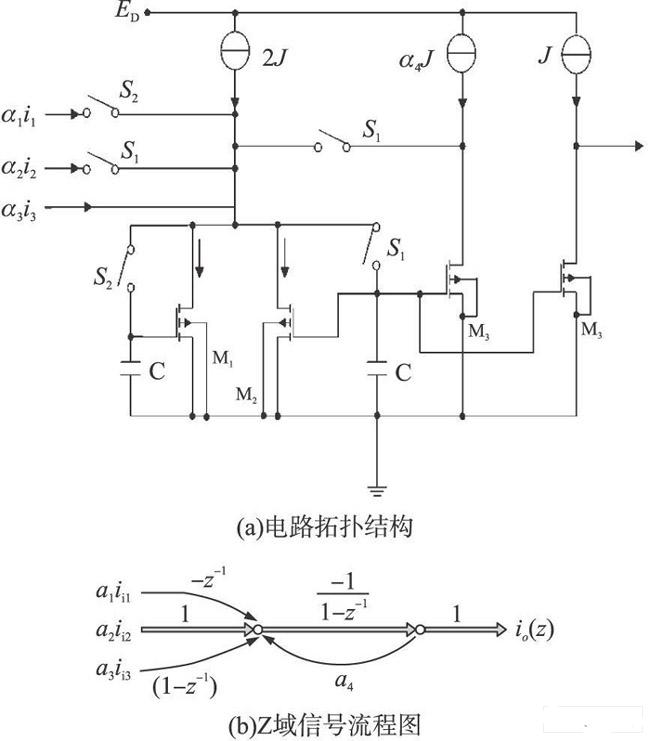
　　图2 通用积分器。

　　1. 2 小波基的选择

　　高斯函数的通用表达式：

　　

 

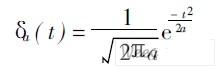
　　式中a是参数， 定义δa(n) q 为δa ( t)的N 阶导数:

　　

 

　　若

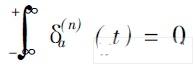
( a 取为一个具体值) 则函数δa (n) ( t )满足小波的可容许性条件， 可采用δa(n) ( t )作为小波基函数， 相应的函数f ( t)在尺度为b， 位置为t处的卷积型小波变换定义为:

 

　　

 

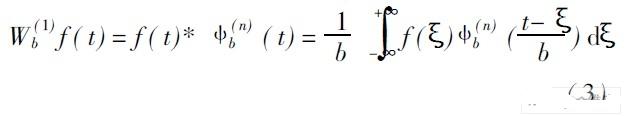
　　可以证明， 其各阶导数也是满足小波函数的容差条件的， 采用高斯函数及其N 阶导数为母小波。

　　1. 3 有理式的Pad 逼近

　　Pad 逼近具有: ( 1)计算简便性——只要获得要逼近函数的Tay lor展开， 再求线性方程组就可以获得其有理逼近式; ( 2)应用广泛——只要函数可以被展成Taylor级数就可以获得其Pad 逼近式。这两个特点使Pad 逼近十分适合于小波滤波器的实现。滤波器的传输函数通常表示为有理分式， Pad 逼近就是从幂级数出发获得有理函数逼近式的一种十分有效而且简洁的方法， 其思想就是对一个给定形式的幂级数构造一个有理函数， 称之为Pad 逼近式， 使其Taylor级数展开有尽可能多的项与原来的幂级数相吻合。

　　Pad 变换的定义 如果存在有理分式函数PL ( s) /QL ( s) ∈ RL，M (PL ( s)与QM ( s)互质)满足：

　　

 

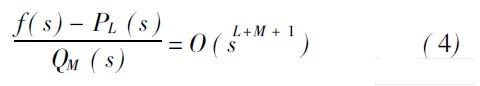
　　及：

　　

 

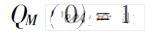
　　0 0 则称PL ( s) /QM ( s)为f ( s)在RL，M 中的Pad 逼近式， 记为[ L /M ] f ( s)， 或简记为[L /M ]。上面的定义给出了求已知函数f ( s)有理表达式逼近方法。若记:

　　

 

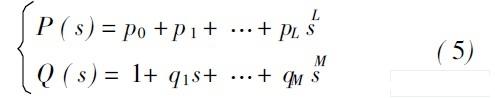
　　QM ( s)乘以式( 3)， 并比较等式两边1， s， s2， ……， sL +M的系数， 可p， p 1， ……， pL 及q0， q1， ……， qM 的线性方程组(称为Pad 方程组):

　　

 

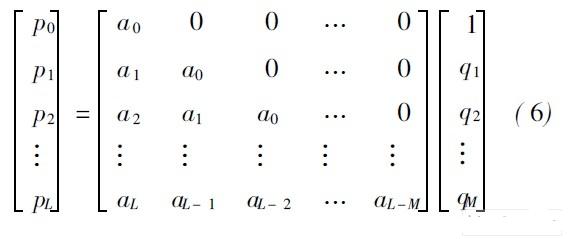
　　及：

　　

 

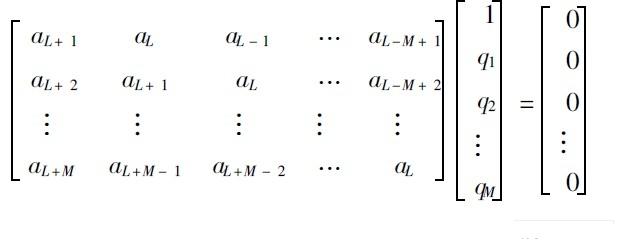
　　其中规定a ≡0， n < 0; qj ? 0， j > M。对方程组( 6)、( 7)求解， 可得到PL ( s)和QM ( s)的系数。根据测不准原理， 高斯函数的时间分辨率与频率分辨率的乘积可以达到理论的最小值， 这样， 用高斯函数族作为小波基函数， 在最大限度上解决了时宽和带宽不相容的矛盾， 在时域和频域均有较好的分辨率。

　　1. 4 双二次积分器的性质

　　在对小波函数的频域表达式进行Pad 变换后，就获得其频域的有理分式逼近。但是此时得到的表达式是S 域的， 而要运用S I基本单元模块电路， 就要对表达式进行变换来转化到Z 域， 这里可通过Z域综合法来实现。采用开关电流基本单元为模块的CAD设计可使电路设计在实现上模块化、直观化，便于灵活现实采用不同S - Z 转化( FD、BD、BL、LD I)时不同结构的电路。FD (前向差分映射) ， BD(后向差分映射) ， LDI(无损离散积分映射) ， BL(双线性积分映射)， 其中性能最好的是BL。

　　为了使电路的设计更加具有灵活性， 这里采用了S I双二次滤波器的性质。即对具有如下传输函数表达式的滤波器， 有：

　　

 

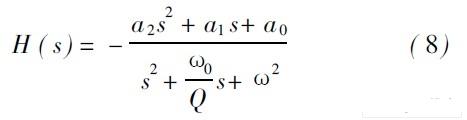
　　其中w0 是滤波器的特征频率、Q 是品质因素。当a0、a1、a2 为不同的值时， 传输函数可以得到二阶低通， 二阶高通， 二阶带通， 二阶全通滤波器函数。而式( 8)又可以由图3所示的信号流程图来表示。

　　

 

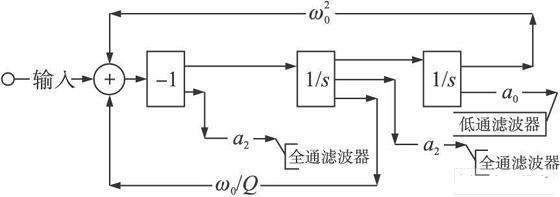
　　图3 双二次滤波器信号流程图

　　在进行S域到Z域的传输函数表达式转换， 采取双线性变换， 得到如图4所示的流程图， 对应的系数就可以很容易的算出来: k0 ~ k4 分别为：

　　

 

　　其中( z+ 1) / ( z- 1)可以用开关电流双线性积分器来实现， 系统通过这种S - Z 域转化可以得到系统的框图， 这里通过把SI电路基本单元框图如双线性积分器作为数据库， 当有理表达式含有该项时让CAD 系统自动调用该结构框图然后级联组成系统。

　　另外由于S - Z 是非线性变换， 还得求Z 域频率， 即频率预翘曲公式来处理:

　　

 

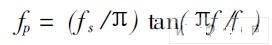
　　其中， f s 为采样频率， fp 为S 域的频率， f 为Z 域的频率。

　　

 

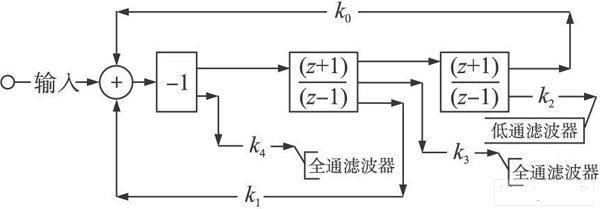
　　图4 双线性积分器实现的双二次滤波器信号流程图

　　2 举例

　　设计举例， 步骤如下:

　　( 1)小波基的选择为确定高斯函数频域表达式的参数及导数阶数N 的值， 这里取高斯函数的一阶导函数为小波基; 即对小波基设置窗口选择a= 2-2， N = 1;( 2)进行Pad 逼近， 选择[L /M ] Pad 逼近， 这里对Pad 逼近窗口设置为[ 3/5] Pad 逼近。就得到分子及分母的各项系数， 写成频域的有理表达式， 如下:

　　

 

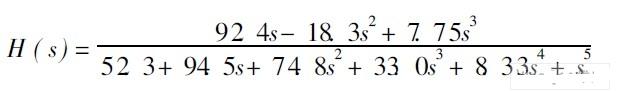
　　改写成为:

　　

 

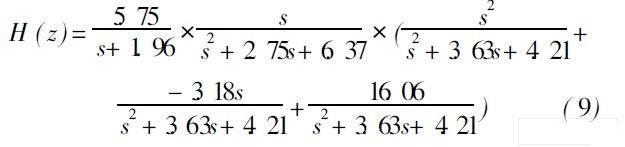
　　( 3)有理式的分解—— Z域综合。选择菜单选项中的BL变换， 对式( 9)应用上面介绍的框图法，各个式子的对应关系如下。

　　通过可以变成H 1 ( z)的形式， 对应一反向有损积分器与同向有损积分器并联相加组成; H 2 ( s ) =对应带通滤波器， 如框图第二行;则对应高通， 带通， 低通滤波器的输出之和， 如框图第三行; 系统的框图就能很容易得到如图5所示。

　　

 

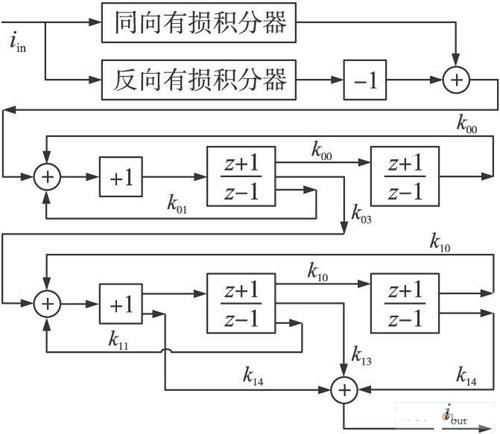
　　图5 系统框图

　　( 4)采用归一化方法， 利用M atlab显示原函数与逼近函数图像对比， 可见逼近度是可以满足一般要求的， 如图6所示。

　　

 

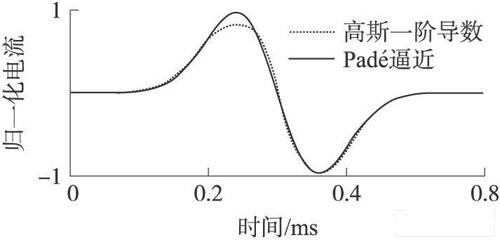
　　图6 Pad 逼近的图像

　　3 结论及结果分析

　　本文首次提出采用开关电流技术实现小波变换电路的一种CAD 方法。采用高斯函数族中的一阶导数为母小波， 采用[ 3 /5 ] Pad 逼近得到其有理表达式。采用[ 3 /5] Pad 逼近能满足要求， 要是想提高逼近度可采用高阶Pad 逼近如[ 6 /10] Pad 逼近， 其均方差(MSE )可小至0. 19 % 10- 4， 但是相应的会提高成本; 又利用了SI基本模块作为单元模块通过编程来得到系统框图结构。