

DC分析示例-使用Python求解网格电流
描述
了解在直流和稳态交流电路分析中使用 Python 和 SymPy 如何帮助加快和简化网格电流和相量电流等计算。
基本电路是线性系统,确定电路中的电流或电压值需要使用线性代数。我发现当我“求解”一个电路(即确定流过电路中所有元件的电流值)时,电路定律的应用早在确定感兴趣的数量之前就已经完成。在短短几分钟内,我们就可以确定一个描述简单电路行为的方程组。然而,手动操作这组代数方程以找到我们正在寻找的量可能需要相当长的时间。
许多学生和教育工作者经常求助于MATLAB来寻求线性系统的帮助,但Python和SymPy包也可以轻松免费地用于分析直流和稳态交流电路。让我们通过一些示例来说明这一点,从 DC 分析开始。
DC 分析示例 - 使用 Python 求解网格电流
图 1 中的电路在现实生活中可能不存在,它没有任何实际用途。
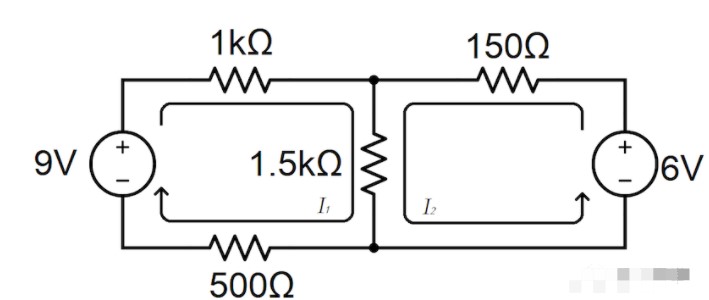
图 1. 直流电路示例电路原理图。
然而,在典型的电路分析教科书中,使用这种带有直流电源的全电阻电路作为在大型电路环境中练习应用基尔霍夫定律和欧姆定律的一种手段。
作为说明,我认为如果您将这些不视为可能是真实的电路,而是将其视为具有特定知识基础和技能组合的人的难题来解决……这会有所帮助……为了好玩!
除此之外,我已经在该电路上绘制了网状电流I 1和 I 2,我们可以使用网状电流分析技术来设计以下等式 1a 和 1b:
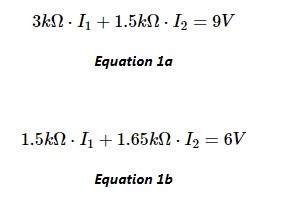
有了这个方程组,我们就有效地完成了电路理论的应用。将这些方程一起处理以求解网格电流 I 1和 I 2的值的剩余任务是纯代数的。让我们将这个方程组转换为矩阵,并使用 Python 为我们研究代数,而不是手动这样做。我们的矩阵将由每个网格电流的电阻系数和方程右侧的电压组成,如图 2 所示。
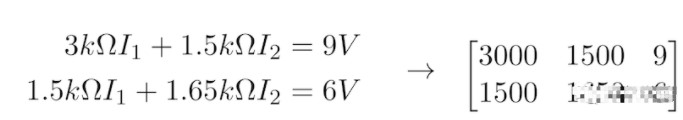
图 2. 描述图 1 电路的 I、R 和 V 关系的矩阵方程。
接下来,我们转向 Python。我使用Google Colaboratory 进行此类计算,因为它可以通过网络访问,并且我需要的所有库都可用。但是,如果您的 Python 环境包含 SymPy 库,您可以使用您喜欢的任何环境。
为了在 Python 中求解我们的方程组,让我们首先导入 SymPy 库,然后定义我们的矩阵,最后使用以下命令计算其简化的行梯形,以确定两个网格电流的值:
from sympy import *
dcEquations = Matrix([[3000, 1500, 9],[1500, 1650, 6]])
dcEquations.rref()
这会产生以下输出:
(Matrix([
[1, 0, 13/6000],
[0, 1, 1/600]]), (0, 1))
这些代码片段告诉我们,I 1的值为 13/6000 A 或 2.17 mA,而 I 2的值为 1/600 A 或 1.67 mA。
使用 Python 的稳态交流分析示例
我们用于分析图 1 中的直流电阻电路的方法也可以用于分析稳态交流电路,并且 在纸上设计一个实际上可以服务于实际目的的交流电路并不需要花费太多精力。图 3 显示了一个带有两个无功负载(电感器)的电路,每个负载都可以代表一个用于空调单元、污水泵、冰箱压缩机或其他家用电器设备的电机。
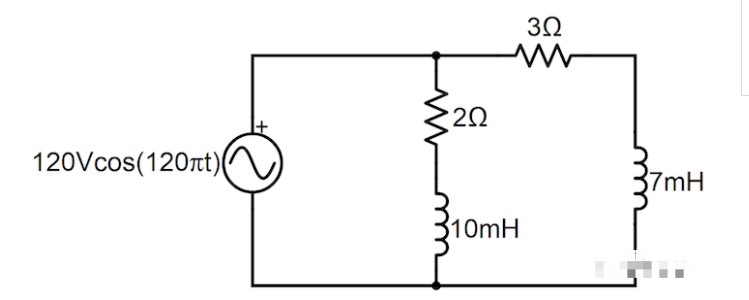
图 3. 具有两个无功负载的稳态交流电路示例。
图 3 中的电路称为“稳态”交流电路,因为它的电源具有固定频率和恒定幅度。从这里开始,我们需要将电路中的电感转换为阻抗(以欧姆为单位),以便我们可以使用网格电流方法来分析其稳态行为。因此,我们根据公式 2 计算电路中电感器的阻抗,使用源的驱动频率为 ω (120π rad/s)。
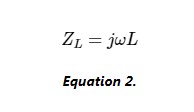
在图 4 中,我们用每个无源元件的阻抗和相量网格电流 I 1和 I 2重新绘制了电路。
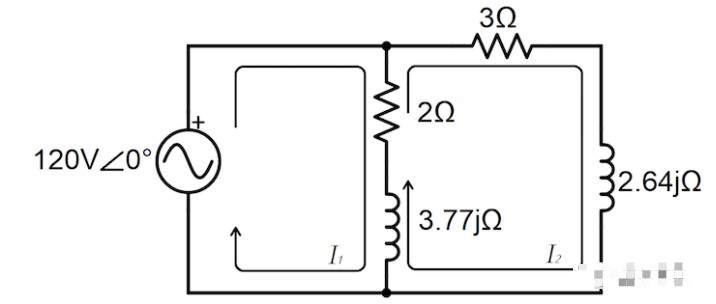
图 4. 将电感转换为阻抗后的图 3 的交流电路。
就像我们对图 1 中的电路所做的那样,我们可以使用基尔霍夫电压定律和欧姆定律推导出与图 4 中电路中的元件和网格电流相关的方程组。方程 3a 和 3b 构成了该系统。
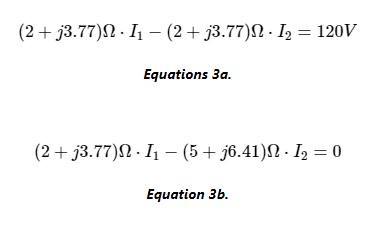
同样,用于求解图 4 电路中网格电流的其余过程是纯代数。该方程组的矩阵形式如图 5 所示。
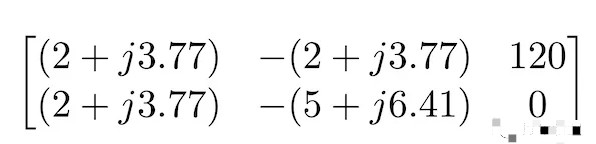
图 5. 等式 3a 和 3b 的矩阵表示图 4 的稳态交流电路。
Python 中的以下命令将为图 4 中电路中的网格电流值求解该方程组。请注意,我们可以在矩阵定义中使用“j”而无需任何特殊努力,因为“j”在 SymPy 中定义为复空间中的虚单位。
from sympy import *
acEquations = Matrix([[2+3.77j,-(2+3.77j), 120],[2+3.77j, -(5+6.41j), 0]])
acEquations.rref()
这会产生以下输出:
(Matrix([
[1, 0, 35.7203044893402 - 44.6772284258869*I],
[0, 1, 22.5428313796213 - 19.8376916140667*I]]), (0, 1))
这告诉我们相量电流 I 1和 I 2分别为 (35.72 – j44.68)A 和 (22.54 – j19.84)A。请注意 Python 如何将虚数单位表示为“I”而不是“j”。为了将这些转换为时间相关函数,我们应用了一点三角函数来找到它们各自的幅度和相位。I 1的幅度和相位通过等式 4a 和 4b 求得:
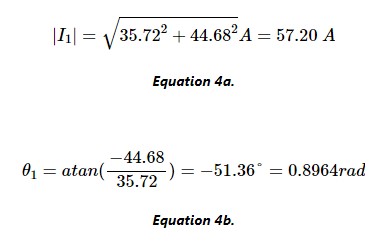
类似地,根据等式 5a 和 5b 求出I 2的幅度和相位:
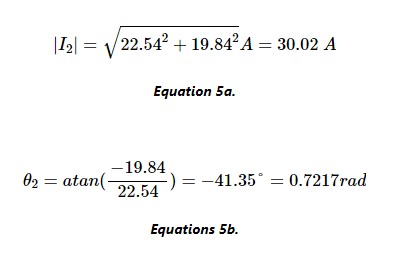
最后,给定这些幅度和相位,我们确定 I 1和 I 2的函数形式:

Python 和 SymPy 对直流和稳态交流分析的好处
请注意,稳态交流分析确实需要预先从电感(和/或电容)转换为复阻抗以及之后从相量形式转换为时间相关形式的额外步骤。然而,使用 Python 应用这种矩阵技术在求解交流电路时比直流电路为我们节省了更多的计算时间,因为 Python 甚至可以为我们处理复杂的代数,轻松处理增加的虚数维度。
对于直流和稳态交流电路分析,可以轻松使用 Python 和 SymPy 库来减少确定所需值所需的工作量。虽然这些示例中分析的电路相对简单,但该技术可以扩展到具有更多网格的更复杂电路。以这种方式使用 Python 不仅可以减少解决电路问题所花费的时间,而且还可以帮助学生在练习新学习的网络分析技术时在心理上区分电路理论和纯代数。
-
60个重要的Python小示例2022-10-26 937
-
如下电流检测电路具体是怎么分析的?2024-03-03 8904
-
matlab的根轨迹、增益选择、方程求解和演示示例命令2009-09-22 8042
-
电源网格的电压下降和电迁移(EMI)效应分析2009-10-23 7391
-
HFSS求解器的主要特点2019-06-28 3315
-
网格电流分析电路2020-10-05 5931
-
IE和FEBI求解器详解及对比2017-11-22 6938
-
python代码示例之基于Python的日历api调用代码实例2018-09-06 1572
-
Python使用示例程序和工程文件免费下载2020-06-15 1025
-
HFSS的IE和FEBI求解器的详细资料概述2020-11-06 1431
-
数列极限的求解方法及案例分析2021-03-24 857
-
机器学习必学的Python代码示例集2021-06-21 1464
-
对于网格做尽量简单化的应用技术揭秘2021-10-28 1711
-
支路电流法是以什么为求解对象2024-08-08 3489
-
使用DC/DC模拟确认线圈电流的方法和选定最佳线圈的示例2024-08-20 1112
全部0条评论

快来发表一下你的评论吧 !

