了解电子电路中的温度漂移

了解电子电路中的温度漂移，即电阻器和放大器。我们还将介绍闪烁噪声的影响如何发挥作用以及漂移如何限制信号平均的有效性。

即使在固定的电气条件下(电源电压、输入和负载)，电子电路也不是完全稳定的，因为它们往往会随着时间和温度而漂移。这些与理想行为的偏差会给精密测量增加相当大的误差。为了深入了解电子产品中的温度漂移，本文简要介绍了电阻器和放大器的温度行为。我们还将讨论闪烁噪声的影响可能不容易与输出中的温度引起的漂移区分开来。最后，我们将讨论漂移会限制信号平均技术的有效性，该技术通常用于提高可重复测量的准确性。

电阻温度漂移——电阻温度系数

作为最简单的电子元件类型，电阻器可能被忽略为高性能电路中的误差源。但是，电阻的值不是恒定的，会随着温度和时间而变化。例如，如果电阻器的温度系数为 ±50 ppm/°C，并且环境温度比参考温度(室温)高 100 °C，则电阻器的值可能会发生 ±0.5 % 的变化。

幸运的是，在许多应用中，电路精度取决于两个或多个电阻的比率，而不是单个电阻的绝对值。在这些情况下，可以使用匹配电阻网络，例如LT5400。电阻器形成一个共衬底网络，并表现出良好匹配的温度特性。图 1 比较了单个分立电阻器与匹配电阻器网络的温度特性。

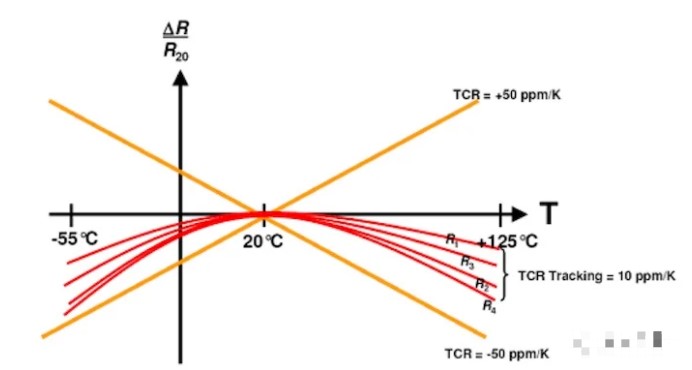
图 1. 匹配电阻器网络温度特性的分立电阻器。图片由Vishay提供

在该图中，橙色线指定了单个 ±50 ppm/°C 电阻器值变化的限制，因为温度从参考温度 (20°C) 沿任一方向变化。红色曲线对应于来自匹配电阻器网络的四个电阻器，它们表现出相似的温度特性。匹配电阻器的温度系数 (TC) 相互跟踪，通常在 2–10 ppm/°C 范围内。具有良好匹配温度特性的电阻器可能是某些精密应用(例如电阻式电流检测)的基本要求。

具有相同温度系数的温度引起的漂移

应该注意的是，即使 TC 值相同，电路中的电阻器也会产生与温度相关的漂移。您可以在下面看到图 2 中的示例。

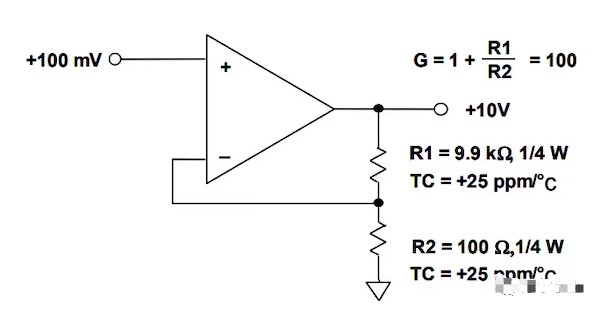
图 2. 创建温度相关漂移的示例。 图片 [已修改] 由Analog Devices提供

在上图中，两个电阻具有相同的 TC (+25 ppm/°C);但是，电阻两端的电压以及因此两个电阻消耗的功率是非常不同的。R 2 = 100 Ω两端的电压为 0.1 V，导致功耗为 0.1 mW。然而，R 1两端的电压为 9.9 V;因此，该电阻器消耗 9.9 mW。假设两个电阻的热阻为125°C/W，R 1和R 2的温度将分别比环境温度升高1.24°C和0.0125°C。这种不相等的自热效应导致两个电阻漂移不同的量。

图 3(a) 显示了另一个示例，其中相同的 TC 不一定能解决温度漂移问题。

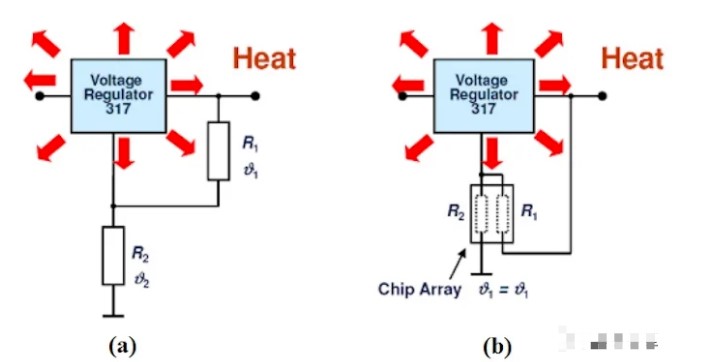
图 3.使用 (a) 分立电阻器用于不同的局部环境温度和 (b) 使用集成电阻器/电阻器阵列用于相同的局部环境温度的示例。 图片由Vishay提供

在上图中，如果设计包含具有相同 TC 的不相等电阻器 (R 1 ≠ R 2 )，则电阻器的自热会产生如上所述的温度引起的漂移。但是，电压调节器可能会导致额外的温度梯度。即使两个电阻器的电阻和 TC 相同(R 1 = R 2和 TC 1 = TC 2)，该温度梯度也会在电阻器中产生不相等的温度漂移。

可以使用电阻阵列来避免上述示例的漂移问题(图 3(b))。通过在单个基板上实施电阻器网络，两个电阻器热耦合并经历相同的环境温度。

其他电路中的温度漂移——运算放大器温度漂移

由于一个简单的电阻器容易受到温度和老化的影响，因此其他更复杂电路的参数也会随着温度和时间而漂移也就不足为奇了。例如，放大器的输入失调电压随温度和时间而变化。这会产生时变误差，限制可测量的最小直流信号。典型通用精密运算放大器的失调漂移范围为 1–10 μV/°C。

如果放大器的偏移漂移限制了我们的测量精度，我们可以考虑使用斩波稳定放大器。这些器件使用偏移消除技术将偏移电压降低到非常低的水平(例如，小于 10 μV)并产生接近零漂移的操作。斩波稳定放大器(例如Microchip 的 MCP6V51)的失调漂移可低至 36 nV/°C。

温度漂移或闪烁噪声 (1/f)?

在非常低的频率下，闪烁噪声是影响电路输出的主要噪声源。闪烁噪声的平均功率与工作频率成反比(这就是为什么闪烁噪声也称为 1/f 噪声)。频率越低，1/f 噪声的平均功率就越高。如果我们测量电路的输出足够长的时间，我们可以捕捉到这种低频噪声的影响。图 4 显示了闪烁噪声在ADA4622-2输出端产生的放大波动。

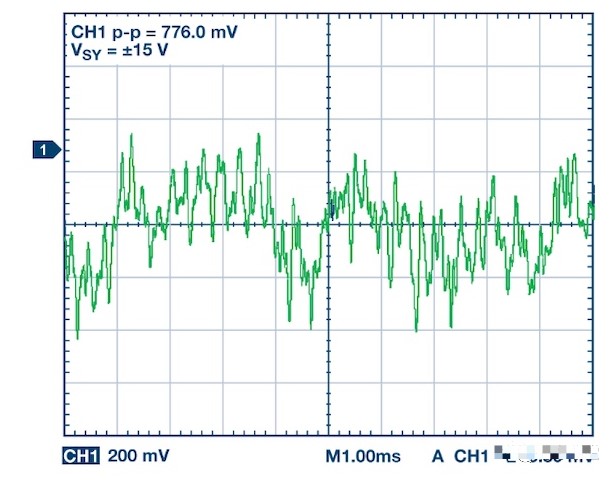
图 4. ADA4622-2 输出闪烁噪声的放大波动。图片由ADI 公司提供

ADA4622-2 是一款精密运算放大器，具有 0.1 Hz 至 10 Hz 噪声，典型值为 0.75 μV pp。上图的波形显示了 ADA4622-2 的 0.1 Hz 至 10 Hz 噪声放大了 1000 倍。如您所见，闪烁噪声导致输出随机缓慢波动。这些波动是由不同于温度或老化引起的漂移的现象产生的。然而，由于其低频特性，1/f 噪声的影响可能不容易与信号中的漂移区分开来。

在运算放大器的情况下，失调漂移和 1/f 噪声都会在输出端引起缓慢的误差。这就是为什么使用失调消除技术来减少失调漂移的零漂移运算放大器在输出端没有 1/f 噪声的原因。图 5 比较了连续时间放大器和零漂移放大器的 1/f 噪声。

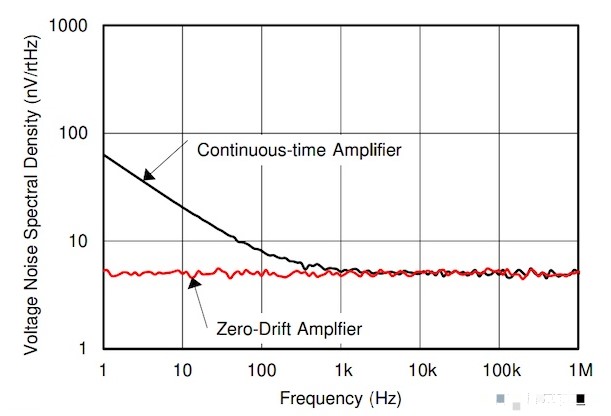
图 5. 连续时间放大器与零漂移放大器的噪声。图片由TI提供

漂移会限制信号平均的有效性吗?另一种有效的降噪技术是信号平均。如果我们有一个噪声方差为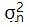的可重复实验，我们可以重复实验 M 次并对相应的输出样本进行平均，以将噪声方差降低到：

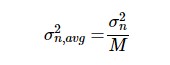
等式 1。 

 

其中 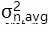表示平均信号的噪声方差。尽管信号平均在某些应用中很有效，但它仍然有其局限性。信号平均基于噪声样本彼此不相关的假设。测量数据中的缓慢漂移可以作为低频相关噪声分量并限制信号平均技术的有效性。在这种情况下，噪声抑制将低于公式 1 预测的值。 此外，根据给定应用中随机漂移的类型，平均信号的方差可能会增加到 M 的某些值以上。

在另一篇文章中，我们将更仔细地研究信号平均技术的这种局限性，并介绍一种有用的统计分析工具，称为艾伦方差，它使我们能够更深入地了解电路的输出如何因不同而趋于漂移闪烁噪声、温度效应等现象。