

ADC失调误差和传递函数
模拟技术
描述
模数转换器 (ADC)有许多规格。根据应用程序的要求,其中一些规范可能比其他规范更重要。DC 规范,例如偏移误差、增益误差、积分非线性 (INL) 和微分非线性 (DNL),在使用 ADC 将缓慢移动的信号(例如来自应变仪和温度的信号)数字化的仪器应用中尤为重要传感器。
本文深入讨论了偏移和增益误差规范。
ADC 传递函数
3 位单极 ADC 的理想传递函数如图 1 所示。
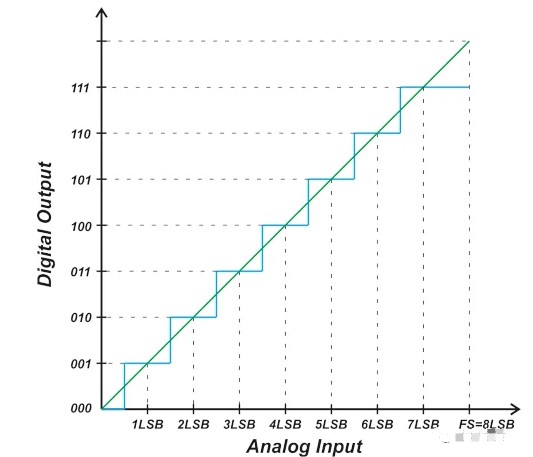
图 1. 3 位单极性 ADC 的数字输出与模拟输入(传递函数)。
理想情况下,ADC 表现出均匀的阶梯式输入输出特性。请注意,输出代码不对应于单个模拟输入值。相反,每个输出代码代表一个宽度等于一个LSB(最低有效位)的小输入电压范围。如上图所示,第一个代码转换发生在 0.5 LSB 处,此后每次连续转换发生在距前一个转换 1 LSB 处。最后一次转换发生在满量程 (FS) 值以下 1.5 LSB 处。
由于使用有限数量的数字代码来表示连续范围的模拟值,因此 ADC 呈现出阶梯式响应,其本质上是非线性的。在评估某些非理想效应(例如失调误差、增益误差和非线性)时,通过通过阶跃中点的直线对 ADC 传递函数进行建模是很有用的。这条线可以用以下等式表示:
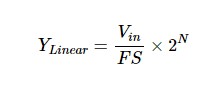
其中 V in是输入电压,N 表示位数。如果我们不断提高 ADC 分辨率(或输出代码的数量),阶梯响应将越来越接近线性模型。因此,可以将直线视为具有无限个输出代码的理想 ADC 的传递函数。然而,在实践中,我们知道 ADC 分辨率是有限的,直线只是实际响应的线性模型。
ADC 失调误差和传递函数
由于内部组件之间的不匹配等非理想效应,ADC 的实际传递函数会偏离理想的阶梯响应。偏移误差使传递函数沿水平轴移动,从而导致代码转换点发生偏移。图 2 中的紫色曲线显示了具有 +1 LSB 偏移的 ADC 的响应。
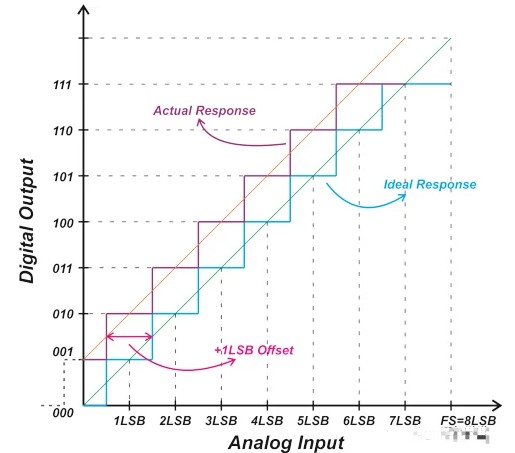
图 2.显示 +1 LSB 偏移、实际响应和理想响应的图表。
对于单极性三位理想 ADC,第一次转换应发生在 0.5 LSB 时,将输出从 000 更改为 001。但是,通过上述响应,ADC 输出在 0.5 LSB 时从 001 转换为 010。理想情况下,001 到 010 的转换应该发生在 1.5 LSB。因此,与理想特性相比,非理想响应向左移动 1 LSB。这被描述为 +1 LSB 偏移误差。考虑非理想响应的线性模型(图中橙色曲线),我们还可以观察到系统在 0V 输入时输出 001,对应于 +1 LSB 偏移。
图 3 显示了失调误差为 -1.5 LSB 的 ADC 的响应。
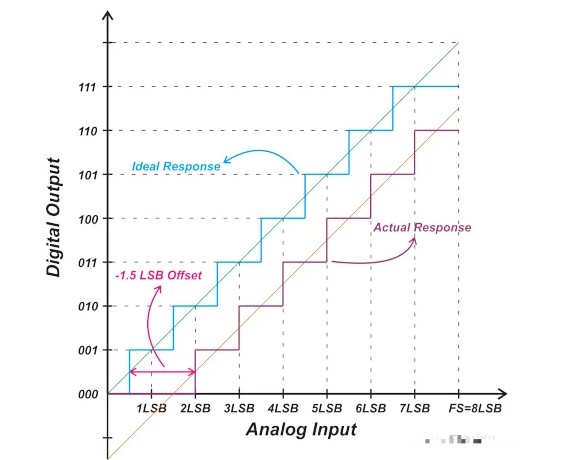
图 3.具有 -1.5 LSB 偏移误差的 ADC 响应。
由于偏移误差使整个传递函数移动了相同的值,因此可以通过从 ADC 输出中减去偏移值来轻松校准。为了确定偏移误差,通常测量第一个代码转换并将其与理想响应的相应转换进行比较。使用第一个代码转换(而不是下一个代码转换)会导致更准确的测量,因为根据定义,偏移误差是指在零伏输入时与理想响应的偏差。
查找 ADC 失调误差示例
考虑一个满量程值为 FS = 5 V 的 10 位 ADC。如果在 8 mV 的输入电压下发生从全零输出代码到 00…01 的转换,那么 ADC 的偏移误差是多少?
对于 FS = 5 V 的 10 位 ADC,LSB 值为 4.88 mV,计算如下:
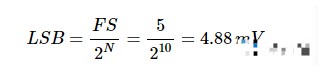
理想情况下,第一次跃迁应发生在 0.5 LSB = 2.44 mV,而测得的响应使该跃迁发生在 8 mV。因此,ADC 的偏移值为 -5.56 mV。偏移误差也可以表示为 LSB 的倍数,如下所示:
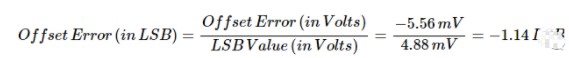
ADC 增益误差
消除偏移误差后,实际响应的第一次转变与理想特性的转变一致。但是,这并不能保证两条特征曲线的其他转变也会发生在相同的输入值处。增益误差指定了最后一次转换与理想值的偏差。图 4 说明了增益误差概念。
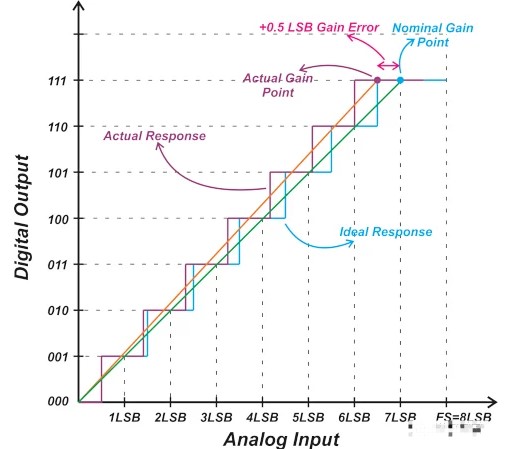
图 4.显示增益误差概念的图表。
让我们将最后一次转换的一半 LSB 定义为“增益点”。消除偏移误差后,理想增益点和实际增益点之间的差异决定了增益误差。
在上述示例中,非理想特性的增益误差为 +0.5 LSB。上图中橙色曲线是非理想响应的线性模型。如您所见,测量增益点和理想增益点之间的差异实际上会改变系统线性模型的斜率。图 5 显示了具有 -1 LSB 增益误差的 ADC 的响应。
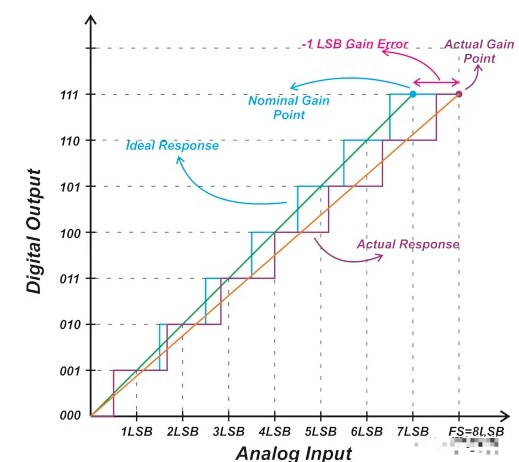
图 5. 具有 -1 LSB 增益误差的 ADC 的响应。
请注意,一些技术文档将增益误差定义为实际增益点与理想 ADC 的直线模型之间的垂直差。在这种情况下,继续图 5 中描述的示例,我们将获得图 6 中的图表。
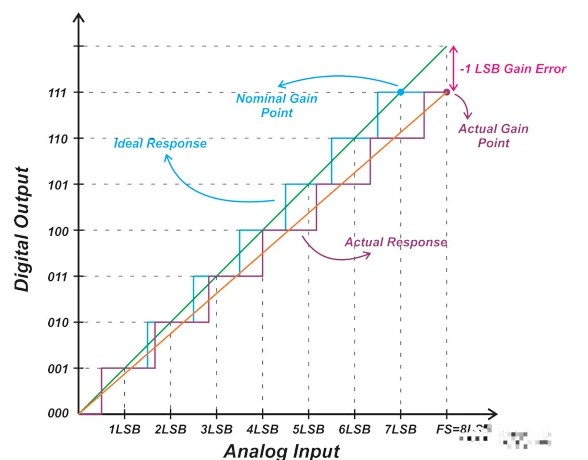
图 6. 增益误差是实际增益点与 ADC 直线模型之间的垂直差。
垂直和水平差异都产生相同的结果,因为理想线性模型的斜率为 1。
查找 ADC 增益误差示例
假设满量程值为 FS = 5 V 的 10 位 ADC 在 4.995 V 时最后一次从十六进制值 3FE 转换到 3FF。假设偏移误差为零,计算 ADC 增益误差。
如上例所示,ADC 的 LSB 为 4.88 mV。理想情况下,最后一次转换应发生在 FS -1.5 LSB = 4992.68 mV。发生转换的测量值为 4995 mV。因此,ADC 的增益误差为 -2.32 mV 或 -0.48 LSB。
用满量程误差表示增益误差
基于上述概念,我们可以根据满量程误差来定义增益误差。这如图 7 所示。
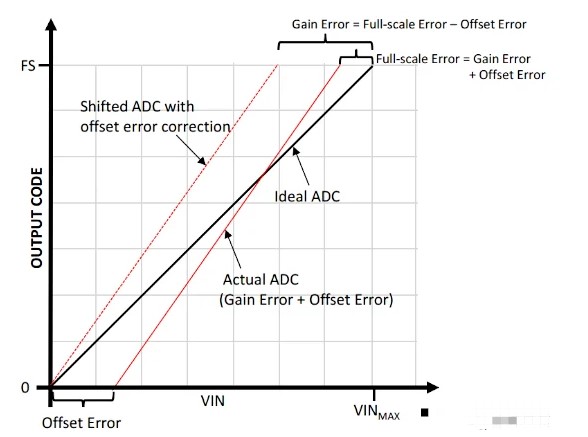
图 7. 满量程误差。图片由Microchip提供
在上图中,实际响应受失调和增益误差的影响。因此,实际最后一次跃迁与理想最后一次跃迁的偏差(用满量程误差表示)包含失调误差和增益误差。为了找到增益误差,我们可以从满量程误差中减去偏移误差:
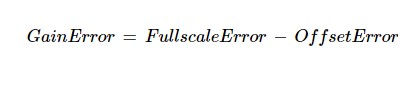
这相当于首先补偿偏移误差,然后测量最后一次转换与理想响应的偏差,从而得出增益误差。请注意,在此特定示例中,增益误差为正,偏移误差为负,导致满量程误差小于增益误差。
定义中的一些 ADC 规范不一致
值得一提的是,一些 ADC 规范在技术文献中的定义并不一致。一个令人困惑的不一致是偏移和增益误差的符号。例如,虽然 Microchip和Maxim Integrated与本文中使用的定义一致,但一些制造商,例如STMicroelectronics (ST),则有所不同。ST 以相反的方式定义这些误差项的符号。来自同一芯片制造商的文件之间也观察到不一致。例如,图 8 取自德州仪器 (TI) 使用相反符号约定的文档。
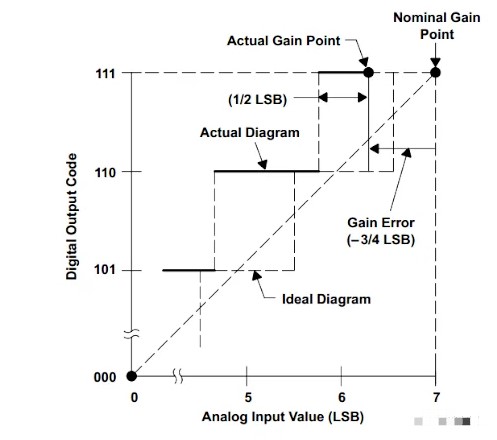
图 8. TI 的 ADC 增益误差示例。图片由TI提供
但是,同样来自 TI 的图 9 使用的定义与本文中使用的定义一致。
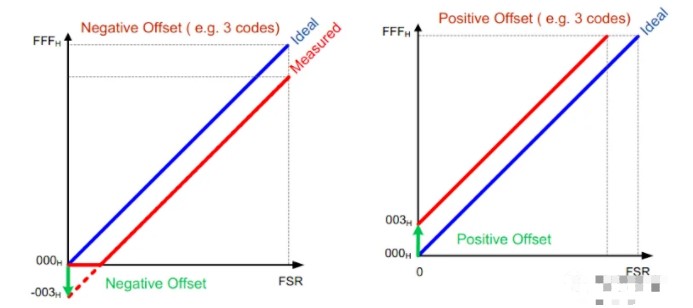
图 9. TI 失调误差示例。图片(改编)由TI提供
图 9(以及整篇文章)中使用的符号约定似乎在各种技术文献中被更广泛地接受。尽管如此。这种不一致可能会导致混淆,但如果您掌握了本文中讨论的基本概念,您就可以绕过这个问题。例如,如果您测量一个 ADC 并观察到它的第一次转换发生在 0.5 LSB 以上(类似于图 3 中描述的情况),您知道应该在 ADC 读数中添加一个适当的正值以补偿偏移误差,无论您使用什么符号约定。
-
传递函数的定义是什么 传递函数的拉氏反变换是什么响应2024-02-01 8387
-
深入探讨模数转换器(ADC)失调和增益误差规格2023-12-04 1016
-
传递函数和控制Block(上)2023-11-17 2414
-
失调误差是如何影响单极性ADC传递函数的?2023-10-24 1228
-
开环传递函数是怎样影响系统的?2023-07-11 5684
-
放大器的传递函数-误差放大器、电压放大器、电流放大器的传递函数导出2023-02-24 4727
-
双极性ADC和差分ADC中的失调误差和增益误差2023-01-27 8490
-
深入探讨模数转换器ADC的失调和增益误差规格2022-12-14 1317
-
双极ADC失调误差和增益误差2022-09-13 4299
-
斜率的传递函数:电压模式的传递函数2018-11-30 2828
-
传递函数的频域辨识2017-10-26 1985
全部0条评论

快来发表一下你的评论吧 !

